
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 1.
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 2.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 3.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 4.
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 5.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 6.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 7.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 8.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 9.
- •Найдите и постройте:
- •Дана функция Показать, что
- •Дана функция и две точки а(х0,,у0) и в(х1,у1);
- •ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 10.
ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 7.
Найдите и постройте:
а)
область определения функции
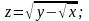
б)
три линии уровня функции
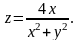
Дана функция Показать, что
Дана функция и две точки а(х0,,у0) и в(х1,у1);
а) вычислить значение z1 функции в точке В;
б) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом;
в) составить уравнение касательной плоскости к поверхности в точке С(х0,у0,z0) и проверить, лежит ли точка в этой плоскости.
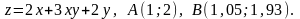
Дана функция
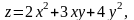 точка
А(2;-2) и вектор
точка
А(2;-2) и вектор

Требуется найти:
а) в точке А;
б) производную в точке А по направлению вектора
Найдите наибольшее и наименьшее значения функции
 в треугольнике, ограниченном прямыми
у = х, у = 4, х = 0.
в треугольнике, ограниченном прямыми
у = х, у = 4, х = 0.
Из куска проволоки длиной = 48 см. сделать каркас
прямоугольного параллелепипеда с наибольшим объемом.
ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 8.
Найдите и постройте:
а)
область определения функции

б)
три линии уровня функции

Дана функция Показать, что
Дана функция и две точки а(х0,,у0) и в(х1,у1);
а) вычислить значение z1 функции в точке В;
б) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом;
в) составить уравнение касательной плоскости к поверхности в точке С(х0,у0,z0) и проверить, лежит ли точка в этой плоскости.

Дана функция
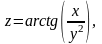 точка
А(3;1) и вектор
точка
А(3;1) и вектор

Требуется найти:
а) в точке А;
б) производную в точке А по направлению вектора
Найдите наибольшее и наименьшее значения функции
 в квадрате
в квадрате
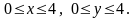 .
.Определить размеры открытого прямоугольного ящика с данным объемом V =62,5 см3 c наименьшей поверхностью.
ЗМмТнб-14 (22.03.01) Контрольная работа № 4. Вариант 9.
Найдите и постройте:
а)
область определения функции

б)
три линии уровня функции

Дана функция Показать, что
Дана функция и две точки а(х0,,у0) и в(х1,у1);
а) вычислить значение z1 функции в точке В;
б) вычислить приближенное значение функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции дифференциалом;
в) составить уравнение касательной плоскости к поверхности в точке С(х0,у0,z0) и проверить, лежит ли точка в этой плоскости.
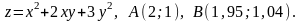
Дана функция
 точка
А(3;-1) и вектор
точка
А(3;-1) и вектор

Требуется найти:
а) в точке А;
б) производную в точке А по направлению вектора
Найдите наибольшее и наименьшее значения функции
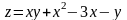 в прямоугольнике
в прямоугольнике
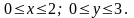
Из куска проволоки длиной = 60 см. сделать каркас
прямоугольного параллелепипеда с наибольшим объемом.
