8.5. Addition of Harmonic Vibrations with Equal

Frequencies and One Direction

An arbitrary vibration system can simultaneously execute several vibrations. Several vibrations in this case add and give the resultant vibration. Addition of vibrations is carried out on the basis of the principle of superposition:

when a subject takes part in several vibrations these vibrations add independently without influencing each other.

Usually under the addition of vibrations it is understood a determination of the law for resultant vibrations of a system participating in several vibration processes.

V e c t o r r e p r e s e n t a t i o n o f v i b r a t i o n

Let us consider the vector A rotating about the point O (Fig. 3.7) with the uniform velocity . Let ₀ be the angle between the vector A and the vertical line at the moment t = 0. The projection of the vector A on the axis x at t = 0 is given by:

x = Asin₀.

At an arbitrary moment of the time t the angle between the vector A and the vertical line is  = (₀ + t) and the projection of the vector A on the axis x is given by:

x = Asin(t + ₀).

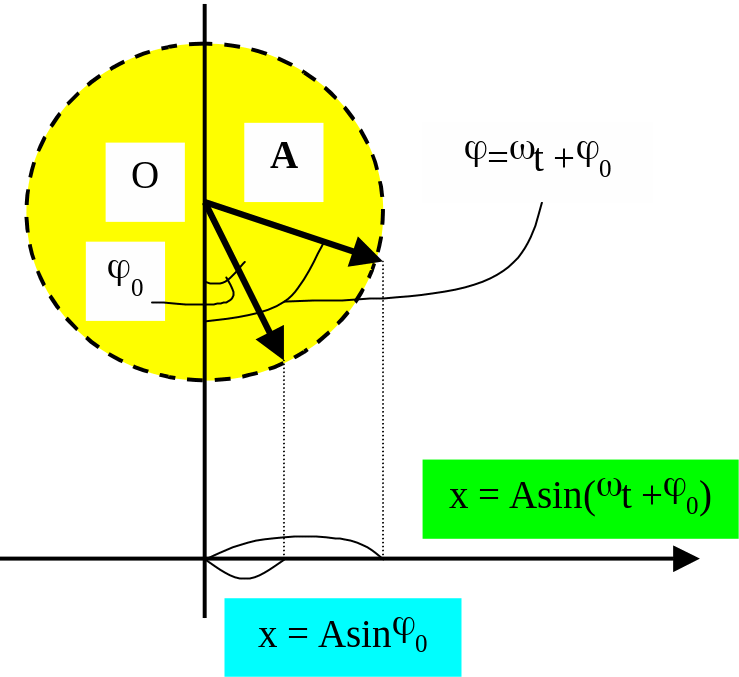
Figure 8.6.

The harmonic vibration can be represented as the projection of the vector A, which rotates about the point O with the uniform velocity .

M o d e l s y s t e m t o s t u d y v i b r a t i o n s a d d i t i o n

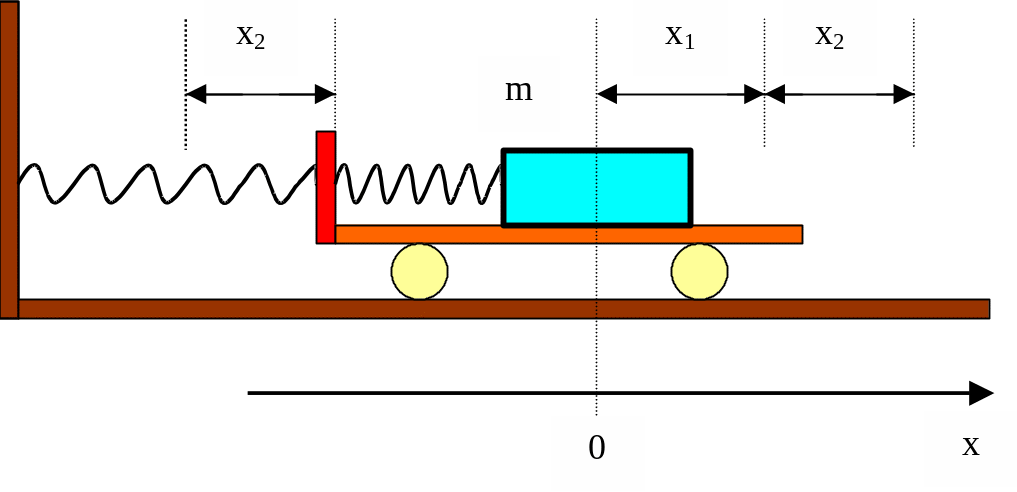
Figure 8.7

The body with the mass m (Fig.8.7) participates in two vibrations and at an arbitrary moment of time the resultant displacement equals to:

x = x₁ + x₂,

where

x₁ = A₁sin₁ = A₁sin(₁t + ₀₁),

x₂ = A₂sin₂ = A₂sin(₂t + ₀₂).

Let us consider the addition of coherent vibrations.

Figure 8.8

Two vibrations x₁ and x₂ are called coherent vibrations if difference of their phases does not depend on time:

From the expression

we can find that the difference of phases does not depend on time in the case when ₁ = ₂.

For the sum of vibrations the vector A(t) corresponds (Fig. 3.9):

A(t) = A₁(t) + A₂(t).

Then (when ₁ = ₂ = ):

x = x₁ + x₂ = A₁sin(t + ₀₁) + A₂sin(t + ₀₂) = Asin(t + ₀).

Using the theorem of cosines we can obtain (Fig. 3.9):

A² = A₁² + A₂² + 2A₁A₂cos(₀₁ - ₀₂),

The addition of two harmonic coherent vibrations of one direction gives the harmonic vibration with the same frequency and its amplitude depends on the amplitudes and initial phases of separate vibrations.

8.6. Addition of Perpendicular Vibrations

T he model system for consideration of perpendicular vibrations is shown in Fig.8.9.

Figure 8.9

Laws of vibrations with perpendicular directions are:

x = A₁sin₁ = A₁sin(t + ₀₁),

y = A₂sin₂ = A₂sin(t + ₀₂).

At arbitrary moment of time the body is located at the distance r from the origin of Cartesian framework:

Providing simple transformations of the following expressions it is easy to obtain the general law of the body motion in this case:

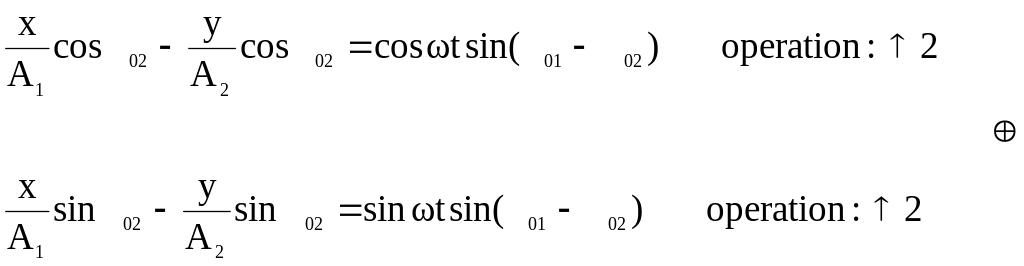
After mentioned operations the general equation of ellipse was evaluated:

Note that (₀₁ - ₀₂) = (₁ - ₂).

The analysis of resultant equation.

1). If (₁ - ₂) = /2, then

and the trajectory of the resultant motion is given in Fig. 8.10.

F igure 8.10

2). If (₁ - ₂) = 0, then

a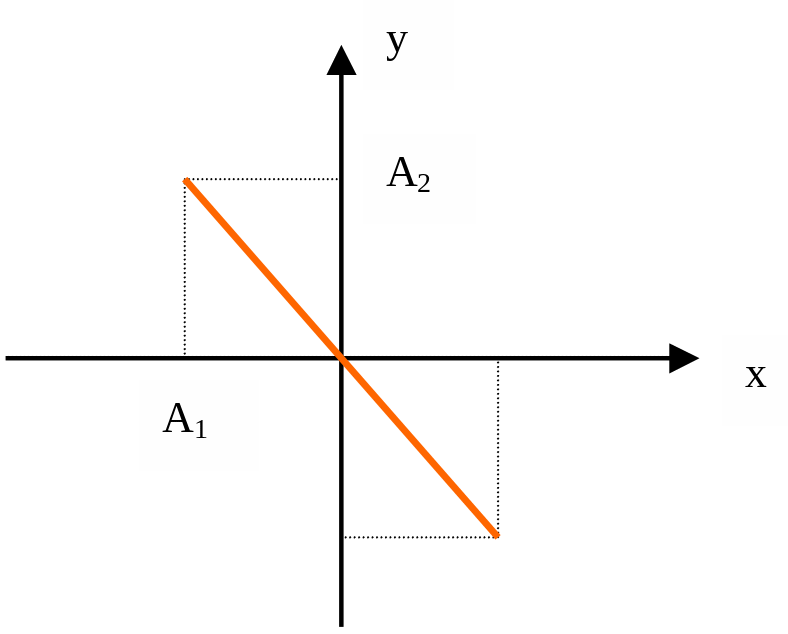 nd the trajectory of the resultant motion is given in Fig. 8.11.

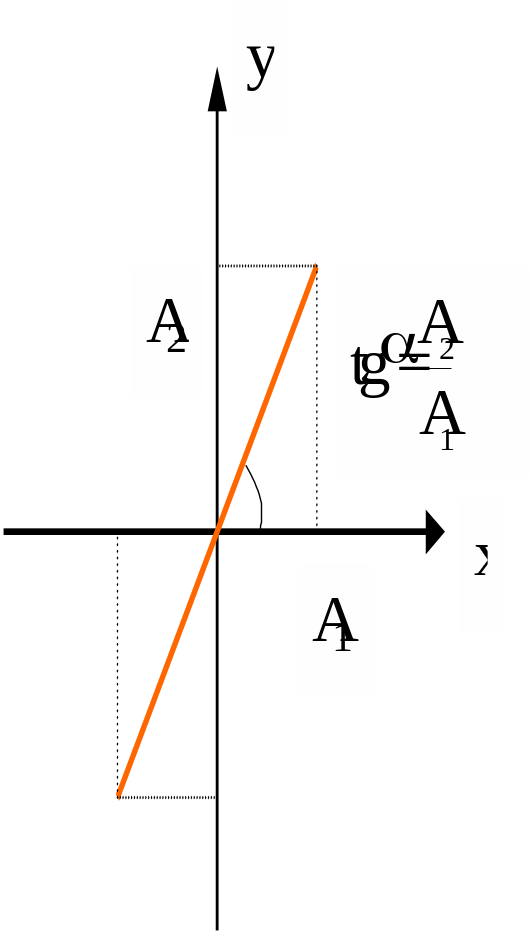Figure 8.11 Figure 8.12

3). If (₁ - ₂) = , then

and the trajectory of the resultant motion is given in Fig. 8.12.

A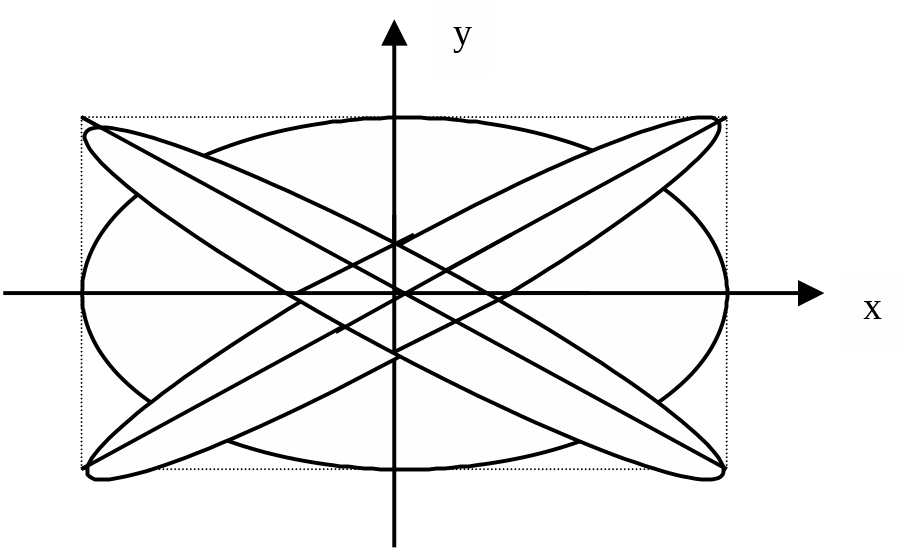 s a result of the addition of two coherent perpendicular vibrations we obtain the movement around the ellipse. Only for the cases when (₁ - ₂) equals to 0 or  we obtain vibrations again, but their direction differs from the directions of the added vibrations (Fig. 8.13).

Figure 8.13