5.7. Perfectly Elastic Collisions

When two bodies collide, the laws of impulse conservation and energy conservation are both always applicable. But in some collisions a part of the kinetic energy of the bodies is transformed into some non-mechanical forms of energy such as heat or sound. In this case the application of the law of energy conservation to the problem becomes exceedingly difficult because many kinds of energy may be involved, some of which are difficult to measure.

If a steel ball is dropped on a steel plate, the ball and the plate are distorted during the action on the impulsive forces, but they return to their original shapes and the ball springs away from the plate. In this case the bodies are only temporary deformed and they regain their original shapes immediately after the collision. Bodies which return to their original shapes after the collision are said to be elastic.

The perfectly elastic collision is an impact after which the shapes of the bodies completely regain, the movements of bodies are independent and mechanical energy does not transform into other forms of energy.

L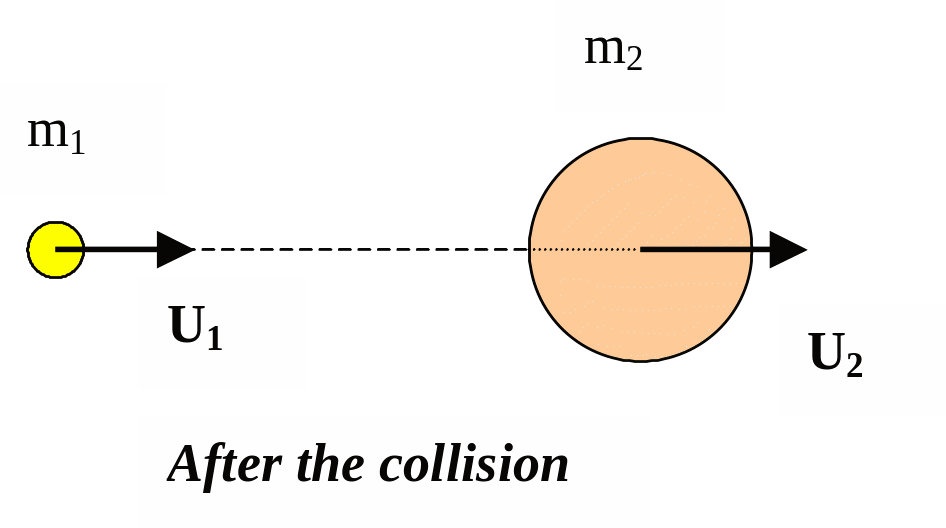 et us consider the following closed and conservative system.

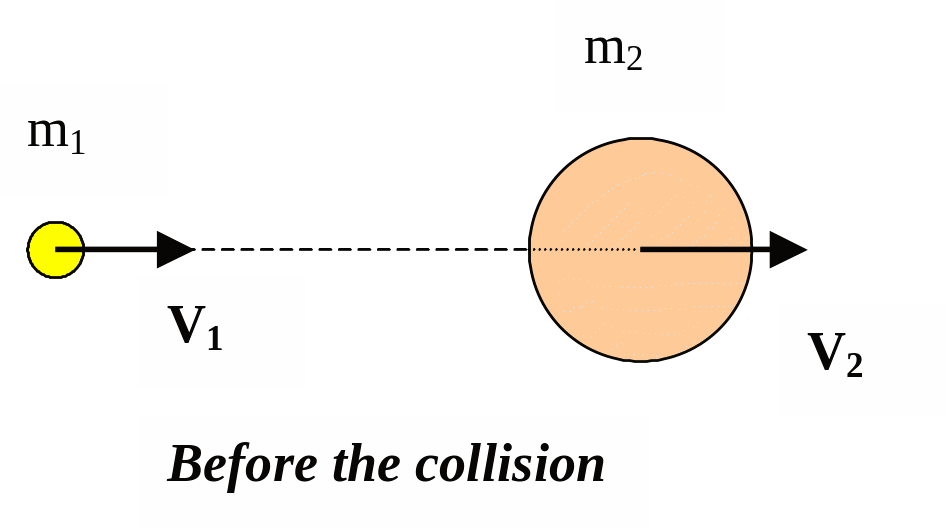
Figure 5.4

In a perfectly elastic collision both the energy and the impulse are conserved. If two bodies collide along the line connecting their centers of mass (Fig. 5.4) we can write:

the law of the energy conservation

m₁v₁² /2 + m₂v₂² /2 + W_p = m₁u₁² /2 + m₂u₂² /2 + W_p,

the law of the impulse conservation

m₁v₁ + m₂v₂ = m₁u₁ + m₁u₂.

For projection on the axis OX:

m₁(u_1x² – v_1x²) = - m₂(u_2x² – v_2x²),

m₁(u_1x – v_1x) = - m₂(u_2x – v_2x).

In the result of dividing of the first equation on the second one we obtain:

u_1x + v_1x = u_2x + v_2x.

Hence

Special cases:

1. if m₁ = m₂, then u_1x = v_2x, u_2x = v_1x, namely the bodies are changing by their velocities.

2. if m₂m₁ and v₂ = 0 then u_1x ≈ - v_1x, (u_2x ≈ 0, namely the first body springs away from the second one).

5.8. Completely Inelastic Collisions

I n completely inelastic collision the two bodies stick together after they have made contact and, as consequence, both have the same final velocity.

Figure 5.5

Conservation of the impulse alone is sufficient to permit us to compute the final velocity if the masses and initial velocities are known (Fig. 5.5):

m₁v₁ + m₂v₂ = (m₁ + m₂)u.

Hence,

The alteration of energy of completely inelastic collision:

It is easy to obtain that ∆W is maximal for the case when u = 0.

HOME – READING

Famous people of science and engineering

Sikorsky Igor Ivanovich was a well-known aircraft engineer and manufacturer.

Sikorsky was born in 1889 in Kiev, in the Ukraine, and got his education at the naval college in St. Petersburg, and later in Kiev and Paris. He was the first to make experiments in helicopter design. In 1913 he designed, built, and flew the first successful aeroplane. Later he built military aircrafts for Russia and France.

In 1919 Sikorsky moved to the United States and later helped to organize an aircraft company that produced series of multiengine flying boats for commercial service. Sikorsky became an American citizen in 1928. In the late 1930s he returned toссссdeveloping helicopters and produced the first successful helicopter in the west. Helicopters designed by Sikorsky were used mostly by the US Army Air Forces during World War II. He died in 1972 at the age of 83.

Tupolev Andrey Nikolayevich, famous aircraft was born in 1888. He graduated from the Moscow Higher Technical School, where he designed the first Russian wind tunnel. He helped to found the Central Aerohydrodynamics Institute in 1918 and later worked as the head of its design bureau. During his career directed the design of more than 100 military and commercial aircraft, including the TU-2 and TU-4 used in the World War [I. In 1955 he designed

TU-104 the first passenger jet airliner. His TU-144 jet liner began its commercial passenger flights in 1974.

ПРАКТИКУМ

з англійської технічної мови