
Закон ома
Соотношение между ЭДС сопротивлением и токами в замкнутой цепи выражается законом Ома, который может быть сформулирован так: Ток в замкнутой цепи прямо пропорционален ЭДС и обратно пропорционален сопротивлению цепи.
Ток в цепи возникает под действием ЭДС. Чем больше ЭДС источника энергии, тем больше ток в замкнутой цепи. Сопротивление цепи препятствует прохождению тока, следовательно, чем больше сопротивление цепи, тем меньше ток.
Закон Ома можно выразить следующей формулой.
I = E/(R+Ro) или E = I(R+Ro) .где
R – Сопротивление внешней части цепи
Ro – внутреннее сопротивление источника
В этих формулах ток I выражен в А, Е – в В, R – Ом
Сопротивление всей цепи R+Ro = E/I.
Закон Ома справедлив не только для всей цепи, но и для любого её участка.
Если участок цепи не содержит источника энергии, то положительные заряды на этом участке перемещаются из точки более высокого потенциала к точке более низкого потенциала. Источник затрачивает известную энергию, поддерживая разность потенциалов между началом и концом этого участка. Эта разность потенциалов называется напряжением между началом и концом рассматриваемого участка.
Таким образом применяя закон Ома для участка цепи получим
I = U/R
Закон Ома можно сформулировать следующим образом.
Ток I на участке электрической цепи равен напряжению на зажимах этого участка, деленному на его сопротивление.
Напряжение на участке цепи равно произведению тока на сопротивление этого участка т.е.
U = I/R
Первый закон кирхгофа
При постоянных токах в цепи ни в одной из ее точек не могут накапливаться электрические заряды, так как это вызвало бы изменение потенциалов точек цепи. Следовательно, электрические заряды, притекающие к какому-нибудь узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу времени. Это положение выражает первый закон Кирхгофа, который формулируется так: сумма токов, направленных к узлу, равна сумме токов, направленных от узла.
Н апример,
для узла А можно записать:
апример,
для узла А можно записать:
I1+I2= I3 +I5,
или, придав уравнению другой вид, получим:
I1+I2+(-I3)+(-I5)=0,
а в общем виде
∑I = 0
т.е. алгебраическая сумма токов в узле равна нулю. При этом токи направленные от узла, считаются отрицательными.
3. Методические указания к решению задачи
Решение этой задачи требует знания закона Ома для всей цепи и ее участков, первого закона Кирхгофа и методики определения эквивалентного сопротивления цепи при смешанном соединения резисторов. Содержание задачи и схемы цепей с соответствующими данными приведены в условии и таблице. Перед решением задачи рассмотрите пример.
 Пример:
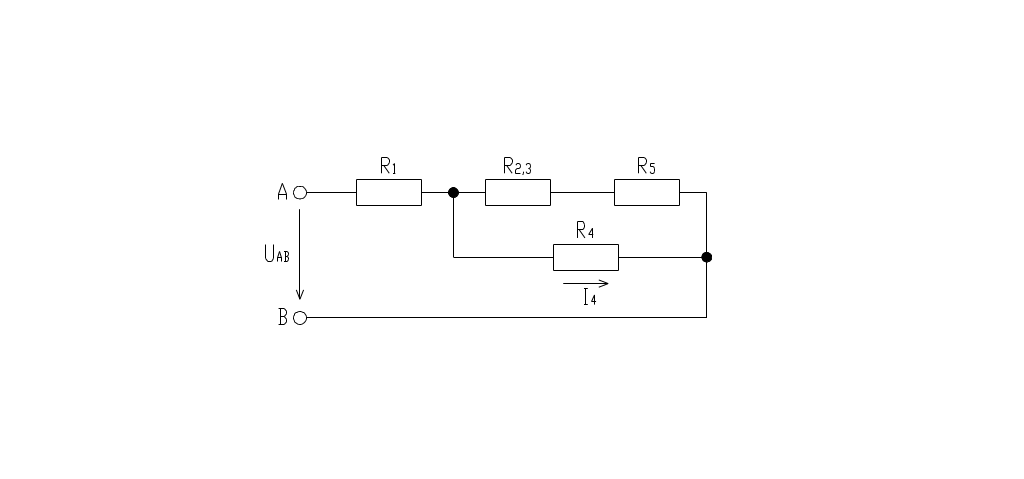
Для схемы, приведенной на рис.а, определить
эквивалентное сопротивление цепи RAB,
токи в
каждом резисторе и напряжение UAB,
приложенное
к цепи. Заданы сопротивления резисторов
и ток I4
в резисторе
R4.
Пример:
Для схемы, приведенной на рис.а, определить
эквивалентное сопротивление цепи RAB,
токи в
каждом резисторе и напряжение UAB,
приложенное
к цепи. Заданы сопротивления резисторов
и ток I4
в резисторе
R4.
R1 = 5 Ом, R2 = 15 Ом, R3 = 10 Ом, R4 = 10 Ом, R5 = 4 Ом, I4 = 5 А.
Рис. а
Решение. Предварительно обозначим стрелкой направление тока в каждом резисторе. Индекс тока должен соответствовать номера резистора, по которому он проходит.
Определяем общее сопротивление разветвления R2, R3. Резисторы соединены параллельно, поэтому
R
2,3=
![]() =
=
![]() =
6 Ом.
=
6 Ом.
Теперь схема цепи принимает вид, показанный на рис. б.
рис. б
Резисторы R2,3 и R5 соединены последовательно, их общее сопротивление
R2,3,5 = R2,3 + R5 = 6 + 4 = 10 Ом.

Соответствующая схема приведена на рис. в.
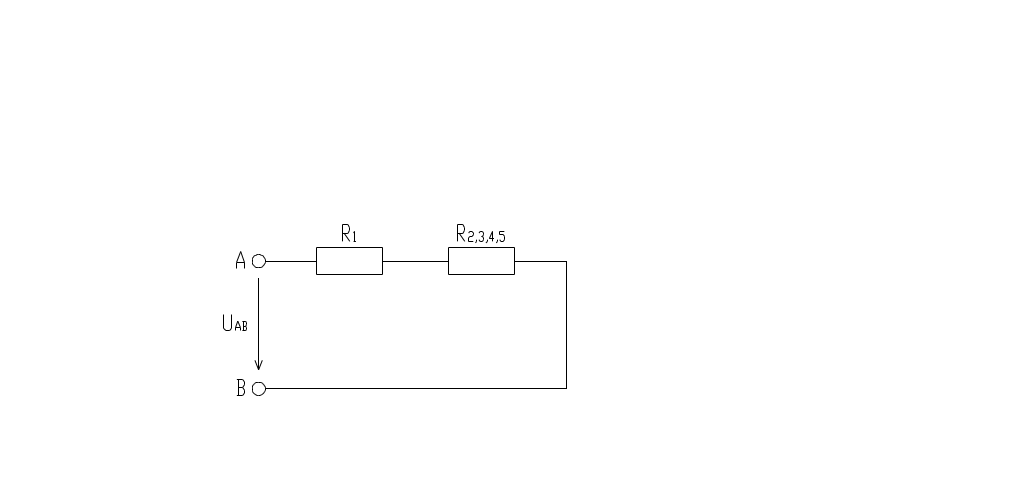
рис. в.
3. Резисторы R2,3,5 и R4 соединены параллельно, их общее сопротивление
![]() R2,3,4,5
=
R2,3,4,5
=
![]() =
5 Ом.
=
5 Ом.
Теперь схема цепи имеет вид, приведенный на рис. г.
4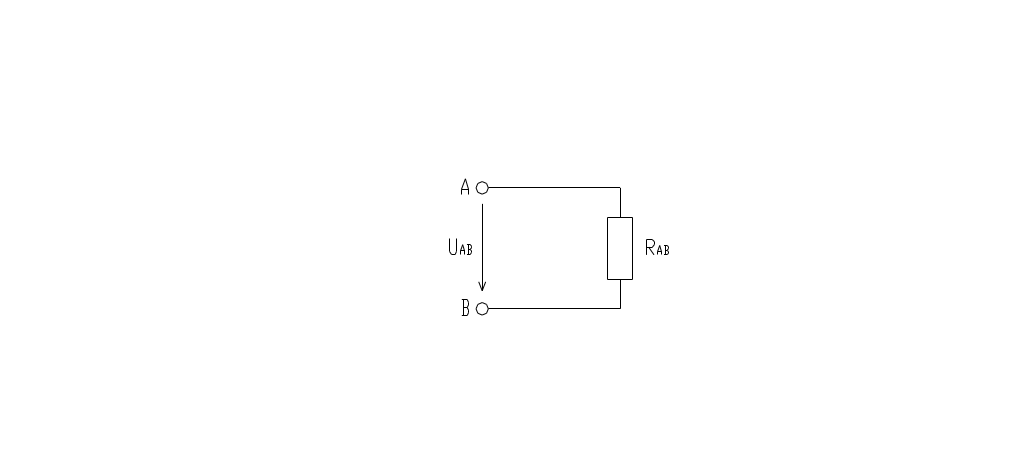 .
Находим эквивалентное сопротивление
всей цепи:
.
Находим эквивалентное сопротивление
всей цепи:
RAB = R1 + R2,3,4,5 = 5 + 5 = 10 Ом. (рис. д)
рис. д
5. Зная силу тока I4, находим напряжение на резисторе R4:
U4
= I4
R4
= 5
![]() 10 = 50 В
10 = 50 В
Это же напряжение приложено к резисторам R2,3 + R5 (рис.1, б). Поэтому ток в резисторе R5
I5
=
![]() =
=
![]() = 5 А.
= 5 А.
6. Находим падение напряжения на резисторе R5:
U5 = I5 R5 = 5 4 = 20 В.
Поэтому напряжение на резисторах R2,3:
U2,3 = U4 - U5 = 50 – 20 = 30 В.
Определяем токи в резисторах R2 и R3:
I2
=
![]() =
=
![]() = 2 А; I3
=
= 2 А; I3
=
![]() =
=
![]() = 3 А.
= 3 А.
Применяя первый закон Кирхгофа, находим ток в резисторе R1:
I1 = I2 + I3 + I4 = 2 + 3 + 5 = 10 А.
Вычисляем падение напряжения на резисторе R1:
U1 = I1 R1 = 10 5 = 50 В.
Находим напряжение UAB, приложенное ко всей цепи:
UAB = I1 RАВ = 10 10 = 100 В
или UAB = UAB + UAB = 50+50 = 100 В.
