Занятие 7 расчет переходных процессов с помощью интеграла дюамеля
Изучите теоретический материал по учебной литературе: [1, с.115–120]; [3, с.231–237] и ответьте на следующие вопросы:
Что такое переходная характеристика?
Какими должны быть независимые начальные условия при расчете переходной характеристики?
Как можно рассчитать переходную характеристику?
Какие размерности может иметь переходная характеристика?
В каких случаях целесообразно рассчитывать переходный процесс с помощью интеграла Дюамеля?
В качестве предварительного задания рекомендуется выполнение задачи 7.1. Для самостоятельной аудиторной работы предназначены задачи 7.2, 7.3, 7.4.
При выполнении, индивидуальных самостоятельных задач 7.1, 7.2 рекомендуется для расчета искомой функции воспользоваться классическим методом.
При решении индивидуальных аудиторных задач 7.4 необходимо обратить внимание на то, что переходная характеристика определяется как реакция на единичное ступенчатое возмущение. Такими возмущениями могут быть либо источник напряжения 1 В, либо источник тока 1 А. Независимые начальные условия (токи в индуктивных катушках и напряжения на емкостях) должны быть нулевыми.
При решении задач 7.3 и 7.5 на основе вычисленных переходных характеристик требуется рассчитать с помощью интеграла Дюамеля указанные искомые функции.
При расчетах рекомендуется использовать следующую запись интеграла Дюамеля:
,
где
–
искомая реакция;
–
заданное
воздействие;
–
переходная
характеристика.
Пример расчета переходного процесса в цепи с помощью интеграла Дюамеля
Пусть
цепь, представленная на рис. 7.1, подключается
к источнику входного напряжения
пилообразной формы (рис. 7.2). Параметры
цепи:
= 5 Ом,
= 10 Ом, L
=
100 мГн. Требуется рассчитать
.
Рис. 7.1. Схема к примеру расчета цепи с помощью интеграла Дюамеля |
Рис. 7.2. Форма заданного входного напряжения |
Определяем переходную характеристику для расчета тока как величину, численно равную этому току при подключении цепи к источнику постоянного напряжения U = 1 B. Расчет ведем, например, классическим методом. В результате расчета получаем
,
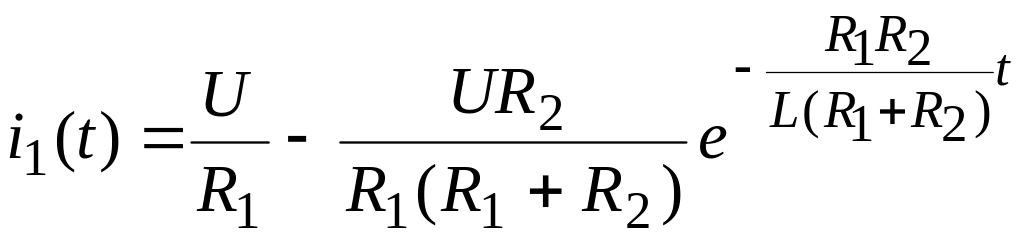тогда
.
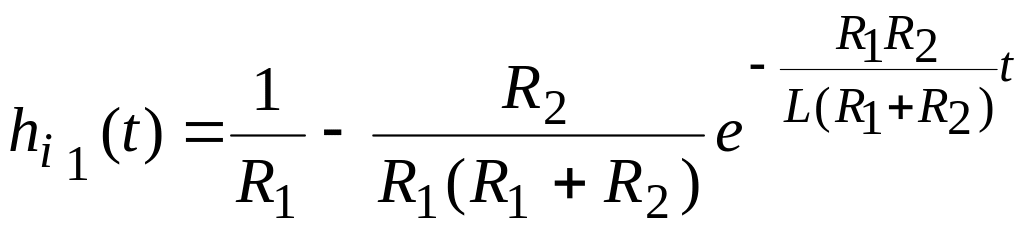Подставляем численные значения параметров схемы:
Ом–1.
С
помощью интеграла Дюамеля вычисляем
ток
,
учитывая, что входное напряжение имеет
форму, показанную на рис. 7.2.
В интервале времени 0 t t1
B,
.
Тогда для первого интервала времени
=
.
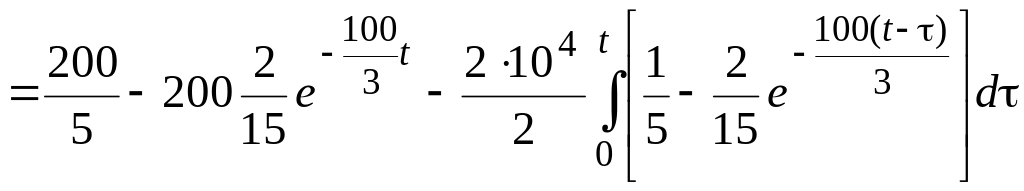В интервале времени t1 t
,
.
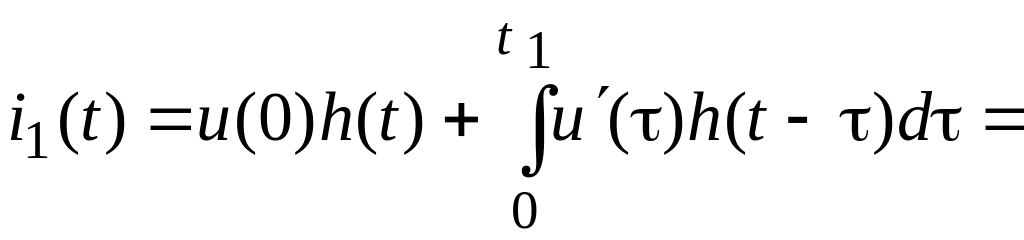
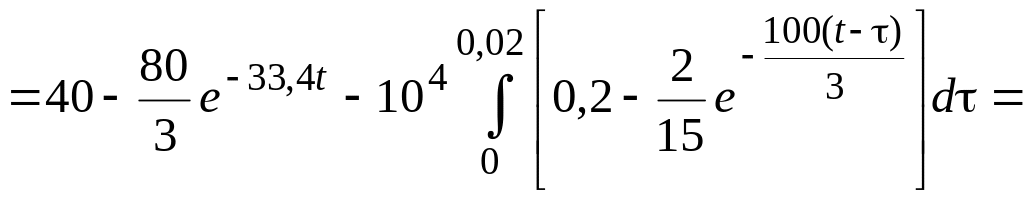
Сравнивая результаты расчета тока в разные интервалы времени, отмечаем, что для первого интервала, когда в цепи действует источник возмущения, решение содержит и принужденную и свободную составляющие.
Во втором интервале времени источник возмущения прекратил действие, поэтому ток содержит только свободную составляющую.
З а д а ч а 7. 1
Определите
ток или напряжение, указанное в столбцах
№ 5, 10 таблицы 7.1, если электрическая
цепь, схема которой показана на рис.
7.3, включается под действие источника
э.д.с. Е=1
В или источника тока J=1
А. Во всех схемах
=
5 Ом. Параметры остальных элементов
указаны в табл. 7.1.
Рис. 7.3. Схемы к задаче 7.1
З а д а ч а 7. 2
Определите переходную характеристику, указанную в табл. 7.3, для схемы из табл. 7.2, соответствующей заданному варианту.
Таблица 7.1
Исходные данные к задаче 7.1
Вариант |
Схема рис.7.3 |
L, мГн |
С, мкФ |
Рассчитать |
Вариант |
Схема рис.7.3 |
L, мГн |
С мкФ |
Рассчитать |
1 |
а |
100 |
– |
|
16 |
г |
– |
100 |
|
2 |
б |
– |
200 |
|
17 |
а |
100 |
– |
|
3 |
в |
100 |
– |
|
18 |
б |
– |
400 |
|
4 |
г |
– |
200 |
|
19 |
в |
100 |
– |
|
5 |
а |
100 |
– |
|
20 |
г |
– |
100 |
|
6 |
б |
– |
200 |
|
21 |
а |
100 |
– |
|
7 |
в |
125 |
– |
|
22 |
б |
– |
400 |
|
8 |
г |
– |
200 |
|
23 |
в |
100 |
– |
|
9 |
а |
50 |
– |
|
24 |
г |
– |
200 |
|
10 |
б |
– |
200 |
|
25 |
а |
100 |
– |
|
11 |
в |
125 |
– |
|
26 |
б |
– |
400 |
|
12 |
г |
– |
100 |
|
27 |
в |
100 |
– |
|
13 |
а |
50 |
– |
|
28 |
г |
– |
200 |
|
14 |
б |
– |
200 |
|
29 |
в |
125 |
– |
|
15 |
в |
100 |
– |
|
30 |
г |
– |
200 |
|
Таблица 7.2
Схемы к задаче 7.2
№ п/п |
Схема |
№ п/п |
Схема |
1 |
|
2 |
|
Продолжение табл. 7.2
№ п/п |
Схема |
№ п/п |
Схема |
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
Окончание табл. 7.2
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
Таблица 7.3
Исходные данные к задаче 7.2
Вариант |
Номер схемы из табл.7.2 |
|
|
|
|
|
|
|
|
Определить |
Гн |
мкФ |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
|||
1 |
1 |
0,03 |
– |
5 |
4 |
5 |
3 |
2 |
2 |
|
2 |
2 |
0,02 |
– |
8 |
7 |
4 |
4 |
7 |
6 |
|
3 |
3 |
0,06 |
– |
2 |
5 |
5 |
3 |
3 |
3 |
|
4 |
4 |
– |
79 |
3 |
5 |
5 |
6 |
6 |
3 |
|
Окончание табл. 7.3
Вариант |
Номер схемы из табл.7.2 |
|
|
|
|
|
|
|
|
Определить |
|
Гн |
мкФ |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
||||
5 |
5 |
0,08 |
– |
4 |
6 |
5 |
5 |
4 |
3 |
|
|
6 |
6 |
0,03 |
– |
2 |
2 |
3 |
3 |
5 |
4 |
|
|
7 |
7 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
8 |
8 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
9 |
9 |
0,05 |
– |
8 |
7 |
4 |
4 |
7 |
6 |
|
|
10 |
10 |
– |
420 |
5 |
4 |
8 |
6 |
7 |
5 |
|
|
11 |
11 |
– |
1300 |
5 |
6 |
3 |
3 |
7 |
6 |
|
|
12 |
12 |
– |
700 |
3 |
3 |
1 |
2 |
2 |
1 |
|
|
13 |
13 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
14 |
14 |
– |
150 |
3 |
2 |
2 |
5 |
1 |
4 |
|
|
15 |
15 |
– |
1000 |
4 |
6 |
4 |
7 |
8 |
6 |
|
|
16 |
16 |
0,7 |
– |
50 |
50 |
40 |
70 |
50 |
70 |
|
|
17 |
15 |
– |
1000 |
4 |
6 |
4 |
7 |
8 |
6 |
|
|
18 |
14 |
– |
150 |
3 |
2 |
2 |
5 |
1 |
4 |
|
|
19 |
13 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
20 |
12 |
– |
700 |
3 |
3 |
1 |
2 |
2 |
1 |
|
|
21 |
11 |
– |
1300 |
5 |
6 |
3 |
3 |
7 |
6 |
|
|
22 |
10 |
– |
420 |
5 |
4 |
8 |
6 |
7 |
5 |
|
|
23 |
9 |
0,05 |
– |
8 |
7 |
4 |
4 |
7 |
6 |
|
|
24 |
8 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
25 |
7 |
– |
810 |
5 |
7 |
6 |
7 |
6 |
8 |
|
|
26 |
6 |
0,03 |
– |
2 |
2 |
3 |
3 |
5 |
4 |
|
|
27 |
5 |
0,08 |
– |
4 |
6 |
5 |
5 |
4 |
3 |
|
|
28 |
4 |
– |
79 |
3 |
5 |
5 |
6 |
6 |
3 |
|
|
29 |
3 |
0,06 |
– |
2 |
5 |
5 |
3 |
3 |
3 |
|
|
30 |
2 |
0,02 |
– |
8 |
7 |
4 |
4 |
7 |
6 |
|
|
З а д а ч а 7. 3
Электрическая
цепь, схема которой выбирается в
соответствии с номером варианта по
табл. 7.4 и рис. 7.5, включается под действие
напряжения, изменяющегося во времени
по заданному закону
.
График изменения входного напряжения
от времени приведен на рис. 7.4, параметры
– в табл. 7.4.
Определите закон изменения во времени величины, указанной в табл.7.4. Задачу решите с помощью интеграла Дюамеля для трех интервалов времени: 0 t t1, t1 t t2, t2 t .
Рис. 7.4. Графики изменения входного напряжения от времени t к задаче 7.3
Рис. 7.5. Схемы к задачам 7.3 и 8.1
Таблица 7.4
Исходные данные к задаче 7.3
Вариант |
Схема (рис. 7.5) |
Форма входного напряжения (рис. 7.4) |
Параметры цепи |
Записать аналитическое выражение |
||
Ом |
Гн |
мкФ |
||||
1 |
а |
а |
5 |
0,1 |
– |
|
2 |
б |
б |
10 |
– |
100 |
|
3 |
а |
в |
5 |
0,1 |
– |
|
4 |
б |
г |
10 |
– |
100 |
|
5 |
а |
д |
5 |
0,1 |
– |
|
6 |
б |
е |
10 |
– |
100 |
|
8 |
б |
б |
10 |
– |
200 |
|
9 |
а |
в |
10 |
0,1 |
– |
|
10 |
б |
г |
10 |
– |
200 |
|
11 |
а |
д |
10 |
0,1 |
– |
|
12 |
б |
е |
10 |
– |
200 |
|
13 |
а |
а |
5 |
0,2 |
– |
|
14 |
б |
б |
5 |
– |
100 |
|
15 |
а |
в |
5 |
0,2 |
– |
|
16 |
б |
г |
5 |
– |
100 |
|
17 |
а |
д |
5 |
0,2 |
– |
|
18 |
б |
е |
5 |
– |
200 |
|
19 |
а |
а |
10 |
0,2 |
– |
|
20 |
б |
б |
5 |
– |
200 |
|
21 |
а |
в |
10 |
0,2 |
– |
|
22 |
б |
г |
5 |
– |
200 |
|
23 |
а |
д |
10 |
0,2 |
– |
|
24 |
б |
е |
5 |
– |
50 |
|
25 |
а |
а |
5 |
0,5 |
– |
|
26 |
б |
б |
5 |
– |
50 |
|
27 |
а |
в |
5 |
0,5 |
– |
|
28 |
б |
г |
5 |
– |
50 |
|
29 |
а |
д |
5 |
0,5 |
– |
|
30 |
б |
е |
5 |
– |
50 |
|
