2.6. Погрішність суми (різниці), добутку, частки, степені, кореня

Теорема.

Абсолютна погрішність алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних погрішностей цих чисел.

Доведення.

Нехай - сума точних чисел і

- сума наближених значень цих чисел.

Абсолютні погрішності відповідно дорівнюють

Різниця між точними та наближеними значеннями дорівнює

.

Перейдемо до модулів різниць -

.

Звідси

Слідство.

Гранична абсолютна погрішність алгебраїчної суми дорівнює сумі граничних абсолютних погрішностей.

, ...

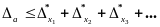
або

При сумуванні чисел різної абсолютної точності рекомендується діяти таким чином:

1. Виділити число найменшої абсолютної точності.

2. Найбільш точні числа округлити таким чином, щоб зберегти в них на один знак більше, ніж у виділеного числа.

3. Виконати підсумовування, враховуючи всі збережені знаки.

4. Результат округлити на один знак.

Приклад. Скласти декілька наближених чисел

а=0,1732+17,45+0,000333+204,4+7,25+144,2+0,0112+0,634+0,0771

В кожному з наведених чисел всі значущі цифри вірні (в широкому сенсі)

204.4
144.2
0.1	7
17.4	5
0.0	0
7.2	5
0.0	1
0.6	3
0.0	8
374.1	9

Відповідь: 374,2

Оцінимо точність результату. Для цього знайдемо повну похибку, яка складається з трьох складових частин:

1. суми граничної погрішності вхідних даних

₁= 0,0001+0,01+0,000001+0,1+0,01+0,1+0,0001+0,001+0,0001=0,221301<0,222;

2. абсолютної величини суми помилок (з врахуванням їх знаків) округлення доданків:

₂= |0,0032+0,000333++0,0012+0,004-0,0029|=0,005833<0,006;

3. остаточної абсолютної погрішності округлення результату ₃= 0,010.

Тобто,

_а=₁+₂+₃0,222+0,006+0,010=0,2380,3.

Звідси сума, яка обчислюється, буде 374,20,3.

Погрішність добутку. Число вірних знаків добутку.

Теорема.

Відносна погрішність добутку декількох наближених чисел, відмінних від нуля, не перевищує суми відносних погрішностей цих чисел.

Нехай

(2.11)

Ці числа мають погрішності

Для оцінки погрішності виконаємо логарифмування виразу (1)

(2.12)

Абсолютна погрішність алгебраїчної суми (2) не перевищує суми абсолютних погрішностей

(2.13)

Використовуючи наближену формулу

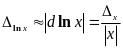(2.14)

отримаємо

(2.15)

звідси

(2.16)

Слідство.

Гранична відносна погрішність добутку дорівнює сумі граничних відносних погрішностей співмножників.

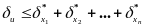
(2.17)

Якщо всі співмножники, крім одного, є точні числа, то згідно з формулою (2.17) випливає, що гранична відносна погрішність добутку співпадає з граничною відносною погрішністю наближеного співмножника. Таким чином, якщо наближеним числом є лише значення множника х_i, то

Зауваження. При множенні наближеного числа х на точний співмножник k гранична відносна погрішність добутку рівняється граничній відносній погрішності наближеного числа х, а гранична абсолютна погрішність в |k| разів стає більше граничної абсолютної погрішності наближеного співмножника.

Із формули (2.17) видно, що гранична відносної погрішності добутку не може бути меншою ніж гранична відносна погрішність найменш точного із співмножників. Тому при перемноженні чисел різної відносної точності рекомендується діяти таким чином:

1. Виділити число з найменшою кількістю вірних значущих цифр (найменш точне число).

2. Більш точні числа округлити таким чином, щоб в них на залишалось на один знак вірних цифр більше, ніж у виділеного числа.

3. В отриманому добутку зберігають стільки значущих цифр, скільки було вірних значущих цифр в найменш точного із співмножників (виділене число).

Приклад. Знайти добуток наближених чисел х₁ = 4,5 та х₂ = 45,273 всі цифри яких вважаються вірними.

Розв’язання. В першому числі маємо дві вірні цифри, а в другому – п’ять. Тому друге число округляємо до трьох значущих цифр. Після округлення маємо х₁ = 4,5 та х₂ = 45,3. Звідси

х₁ х₂ = 4,545,3= 203,85200=2,010²

В результаті залишено дві значущі цифри (другий справа нуль – незначуща цифра, тобто округлюємо до десятків!).

Погрішність ділення.

Теорема.

Відносна погрішність ділення не перевищує суми відносних погрішностей ділимого і дільника.

Нехай Х та У наближені числа і та їх абсолютні погрішності. Для визначеності припустимо Х>0 та Y>0. Необхідно знайти погрішність ділення

(2.18)

Проведемо логарифмування виразу (2.18)

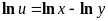
Абсолютна погрішність алгебраїчної суми наближених чисел не перевищує суму складових частин.

Користуючись наближеною формулою

отримаємо

або

Слідство.

Гранична відносна погрішність частки дорівнює сумі граничних відносних погрішностей діленого та дільника.

, , ,

.

Зауваження: Всі правила наближених обчислень, які сформульовані для множення, розповсюджуються і на випадок ділення. Зокрема, якщо одне з чисел (дільник або ділене) відносно точніше другого, то більш точне число округлюється так, щоб у ньому залишилось на одну значущу цифру більше, ніж кількість вірних значущих цифр найменш точного числа. Це ж правило розповсюджується і на випадок, коли приходиться перемножати або ділити декілька чисел. Кінцевий результат, як правило, записується з абсолютною або граничною абсолютною погрішністю. Звідси, якщо ми знаємо відносну або граничну відносну погрішність результату, то згідно з формулою

можна легко визначити абсолютну або граничну абсолютну погрішність результату.

Приклад. Обчислити частку від ділення u=x/y наближених чисел x=5,735 та y=1,23, якщо всі цифри ділимого та дільника вірні в широкому сенсі. Визначити граничну відносну та абсолютну погрішності.

Обчислюємо частку. Так як x=5,735 має чотири вірні цифри, а y=1,23 три, то проводимо обчислення без попереднього округлення: u = 5,735:1,23 = 4,66. В результаті залишаємо три вірні цифри, так як найменш точне число (дільник) має три вірних значущих цифри. Порахуємо граничну відносну погрішність частки, враховуючи, що ,

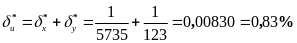
Тоді гранична абсолютна погрішність . Остаточний результат слід записати у вигляді: u= 4,660,04. Зауважимо, що в розглянутому випадку остання значуща цифра є сумнівною, тому що 0,04>0,01. Якщо записувати результат тільки з вірними значущими цифрами, то необхідно провести округлення і врахувати цю погрішність округлення, тобто u₁=4,7; . Тоді u= 4,70,1.

Погрішність степені та кореня (без доказу. Докази – для самостійного опрацювання).

Погрішність степені. Теорема. Гранична відносна погрішність m-ї степені наближеного числа (m – натуральне число) в m разів більше граничної відносної погрішності самого числа.

Слідство. При піднесені наближеного числа в степінь в результаті обчислення слід залишити стільки значущих цифр, скільки вірних значущих цифр є в основі степені.

Погрішність кореня. Теорема. Гранична відносна погрішність кореня m-ї степені наближеного числа в m разів менше граничної відносної погрішності підкореневого числа.

Слідство. При знаходженні кореня наближеного числа в результаті обчислення слід залишити стільки значущих цифр, скільки вірних значущих цифр є в підкореневому числі.