Переход от одного опорного решения к другому. Метод потенциалов

Теорема (признак оптимальности опорного решения). Если существуют m чисел , , …, и n чисел , , …, такие, что для базисных клеток и для свободных клеток, то план , , будет оптимальным планом транспортной задачи.

Числа называются u_i потенциалами пунктов отправления, числа v_j называются потенциалами пунктов назначения.

Группа равенств для базисных клеток используется как система уравнений для нахождения потенциалов. Данная система имеет m+n неизвестных u_i и v_j ( , ). Число уравнений равно m+n-1. Следовательно, чтобы найти ее решение достаточно задать значение одной неизвестной произвольно (например, u₁=0), а остальные найти из системы.

Группа неравенств для свободных клеток используется для проверки оптимальности опорного решения.

Запишем неравенства в виде: .

Числа называются оценками свободных клеток таблицы ТЗ.

Оценки для свободных клеток ТЗ используются для улучшения опорного решения. С этой целью находят клетку (l, k) таблицы, соответствующую max ( , ). Если , то решение оптимальное. Если , то соответствующую клетку вводят в число базисных. Т.к. базисных клеток стало m+n, то по теореме 2 из них можно построить цикл. С помощью цикла улучшают решение. Для этого необходимо расставить в клетках, которые входят в цикл знаки «+» и «–» поочередно, начиная с вновь введенной базисной клетки , в которую ставится знак «+».

В клетках, , где стоит знак «–» выбрать клетку с наименьшей перевозкой, т.е. . Затем осуществляют сдвиг по циклу на величину .

Сдвигом по циклу на величину  называется увеличение объемов перевозок во всех клетках цикла, отмеченных знаком «+», на , и уменьшить – во всех клетках цикла, отмеченных знаком «–», на .

Таким образом, клетка выйдет из числа базисных и получаем новое опорное решение.

Пример. На трех базах A₁, A₂, A₃ находится однородный груз в количестве a₁=30, a₂=40, a₃=20 т. Этот груз необходимо развести четырем потребителям B₁, B₂, B₃, B₄, потребности которых в данном грузе составляют b₁=20, b₂=30, b₃=30, b₄=10, соответственно. Стоимость перевозок пропорциональна расстоянию и количеству перевозимого груза (С – матрица тарифов). Требуется спланировать перевозки так, чтобы их общая стоимость была минимальной.

.

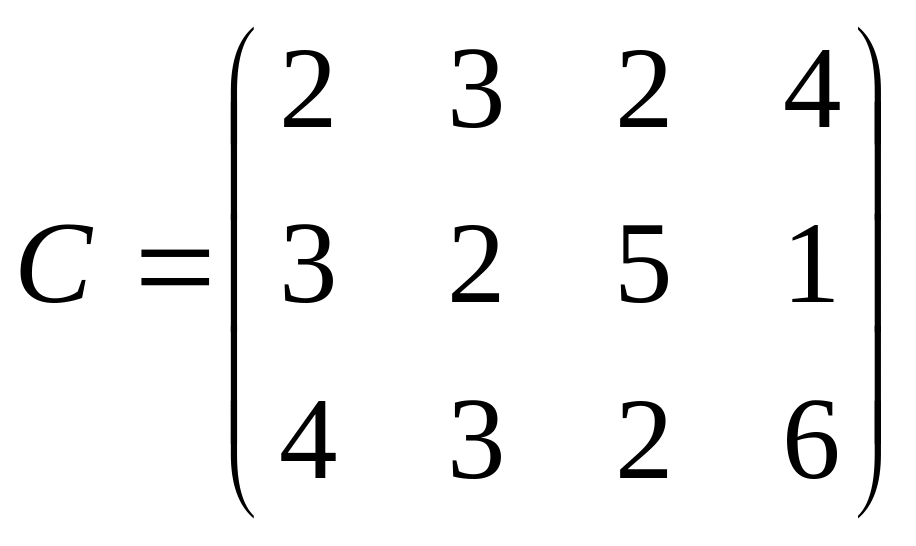Решение:

Базы	Потребители
	B1	B2	B3	B4
A1	2	3	2	4
A2	3	2	5	1
A3	4	3	2	6

Начальное решение находится по правилу «северо-западного угла». Заполним исходную таблицу:

Таблица 1

Базы		Потребители								ai
		B1		B2		B3		B4
	Потенциалы	v1=2		v2=3		v3=6		v4=10
A1	u1=0		2		3		2		4	30
		20		10
A2	u2= -1		3		2	-	5	+	1	40
				20		2 0
A3	u3= -4		4		3	+	2	-	6	20
						10		10
bj		20		30		30		10		90

Число занятых клеток .

Проверим методом потенциалов, является ли полученное опорное решение (план) 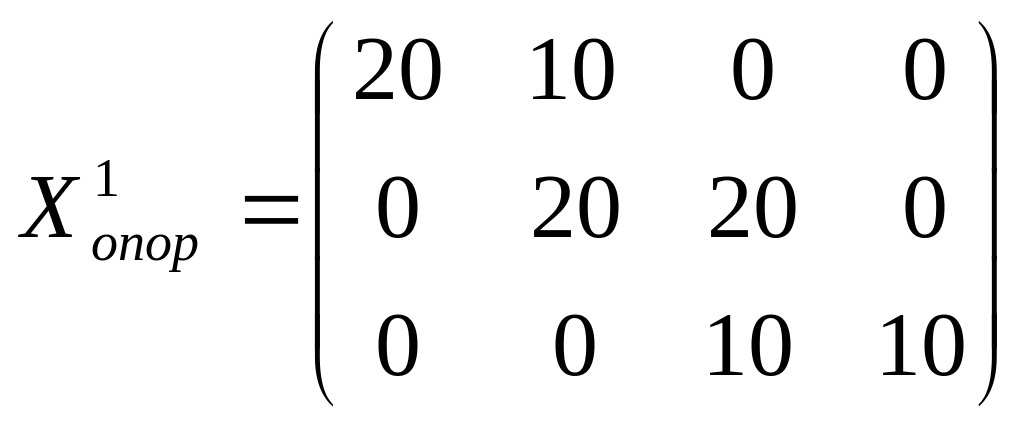– оптимальным? В заполненных клетках должно выполняться условие (данные в таблице 1). В свободных клетках должно выполняться условие .

Номера клеток	Свободные	Условие
1-3		Не выполняется
1-4		Не выполняется
2-1		Выполняется
2-4		Не выполняется
3-1		Выполняется
3-2		Выполняется

Условия оптимальности не соблюдаются в клетках 1-3, 1-4, 2-4. Наибольшая разница несовпадения в клетке 2-4, ее принимаем за основание цикла, поставив в нее знак «+». Строим замкнутый цикл, чередуя в точках поворота знаки «+» и «–». Находим в клетках со знаком «–» , – коэффициент поправки. Улучшаем исходный план, прибавляя коэффициент поправки к клеткам со знаком «+» и вычитая его из клеток со знаком «–», строим новую улучшенную таблицу (таблица 2):

Таблица 2

Базы		Потребители								ai
		B1		B2		B3		B4
	Потенциалы	v1=2		v2=3		v3=6		v4=2
A1	u1=0		2	-	3	+	2		4	30
		20		1 0
A2	u2= -1		3	+	2	-	5		1	40
				20		10		10
A3	u3= -4		4		3		2		6	20
						20
bj		20		30		30		10		90

Число занятых клеток .

Проверим методом потенциалов, является ли полученное новое опорное решение (план) 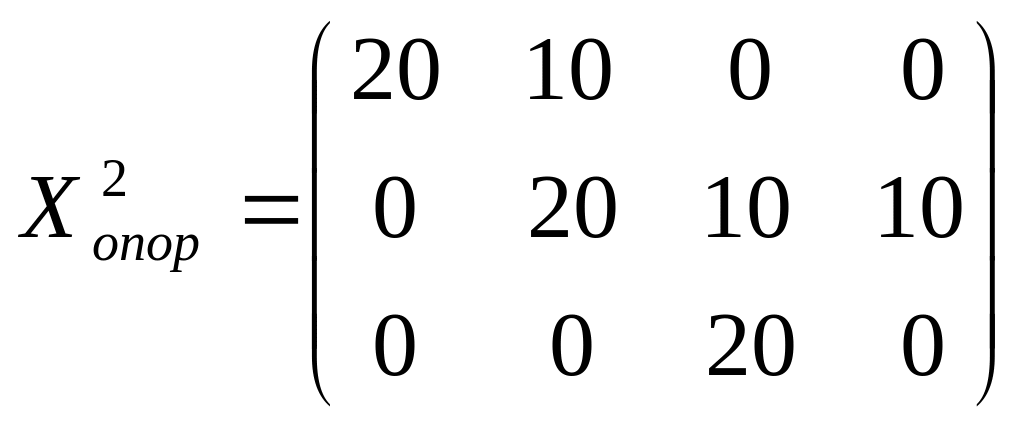– оптимальным? В заполненных клетках должно выполняться условие (данные в таблице 2). В свободных клетках должно выполняться условие .

Номера клеток	Свободные	Условие
1-3		Не выполняется
1-4		Выполняется
2-1		Выполняется
3-1		Выполняется
3-2		Выполняется
3-4		Выполняется

Условия оптимальности не соблюдаются в клетке 1-3. Принимаем клетку 1-3за основание цикла, поставив в нее знак «+». Строим замкнутый цикл, чередуя в точках поворота знаки «+» и «–». Находим в клетках со знаком «–» , – коэффициент поправки. Улучшаем исходный план, прибавляя коэффициент поправки к клеткам со знаком «+» и вычитая его из клеток со знаком «–», строим новую улучшенную таблицу (таблица 3):

Таблица 3

Базы		Потребители								ai
		B1		B2		B3		B4
	Потенциалы	v1=2		v2=3		v3=2		v4=2
A1	u1=0		2		3		2		4	30
		20		0		10
A2	u2= -1		3		2		5		1	40
				30				10
A3	u3= 0		4		3		2		6	20
						20
bj		20		30		30		10		90

Число занятых клеток .

Проверим методом потенциалов, является ли полученное новое опорное решение (план) – оптимальным? В заполненных клетках должно выполняться условие (данные в таблице 3). В свободных клетках должно выполняться условие .

Номера клеток	Свободные	Условие
1-4		Выполняется
2-1		Выполняется
2-3		Выполняется
3-1		Выполняется
3-2		Выполняется
3-4		Выполняется

Данный план перевозок оптимален, т.к. условие для свободных клеток выполняется. Минимальные транспортные расходы составляют:

Ответ: , Z= 170 (д.ед.).