
- •Аналіз довготермінових фінансових операцій: базові концепції і моделі оцінки
- •Фактор часу і оцінка потоків платежів
- •Методи врахування фактору часу у фінансових операціях
- •Оцінка потоків платежів
- •Грошові потоки у вигляді серії рівних платежів (ануїтети)
- •Розробка планів погашення кредитів
- •Запитання для самоконтролю
- •Задачі і вправи
Оцінка потоків платежів
Здійснення практично будь-якої фінансової операції породжує рух грошових коштів: виникнення окремих платежів або множини виплат і надходжень, розподілених у часі.
У
процесі кількісного аналізу фінансових
операцій зручно абстрагуватися від їх
конкретного економічного змісту і
розглядати породжені ними рухи грошових
коштів як числовий ряд, що складається
із послідовності розподілених у часі
платежів
![]() .
Для позначення подібного ряду у світовій
практиці широко використовується термін
потік
платежів,
або грошовий
потік
(cash flow – CF). Окремий елемент такого
числового ряду
.
Для позначення подібного ряду у світовій
практиці широко використовується термін
потік
платежів,
або грошовий
потік
(cash flow – CF). Окремий елемент такого
числового ряду
![]() представляє собою різницю між всіма
надходженнями (притоками) грошових
коштів і їх витратами (відтоками) на
конкретному часовому відрізку здійснення
фінансової операції. Таким чином,
величина
може мати як додатний, так і від’ємний
знак.
представляє собою різницю між всіма
надходженнями (притоками) грошових
коштів і їх витратами (відтоками) на
конкретному часовому відрізку здійснення
фінансової операції. Таким чином,
величина
може мати як додатний, так і від’ємний
знак.
Кількісний аналіз грошових потоків, що генеруються за певний період часу в результаті реалізації фінансової операції або функціонування будь-яких активів, у загальному випадку зводиться до обчислення наступних характеристик:
![]() – майбутньої вартості потоку за n
періодів;
– майбутньої вартості потоку за n
періодів;
![]() – теперішньої
вартості потоку за n
періодів.
– теперішньої
вартості потоку за n
періодів.
Часто виникає необхідність визначення і ряду інших параметрів фінансових операцій, найважливіші із яких:
– величина потоку платежів в періоді t;
– процентна ставка;
– термін (кількість періодів) здійснення операції.
Далі розглянемо найбільш поширені види грошових потоків, їх властивості, а також термінологію автоматизації обчислення перелічених характеристик і параметрів з використанням ППП Excel.
Фінансові операції з елементарними потоками платежів
Найпростіший (елементарний)2 грошовий потік складається із однієї виплати і наступного надходження або разового надходження із наступною виплатою, розподілених – періодами часу (наприклад років).
Прикладами
фінансових операцій з подібними потоками
платежів є термінові депозити, одночасові
позики, деякі види цінних паперів та
ін. Неважко помітити, що числовий ряд в
цьому випадку складається всього із
двох елементів –
![]() або
або
![]() .
.
Операції з елементарними потоками платежів характеризуються чотирма параметрами – FV, PV, і . Величина будь-якого із них може бути визначена за відомим значенням трьох інших.
Майбутня величина елементарного потоку платежів
Розглянемо технологію обчислення майбутньої величини елементарного потоку платежів на наступному прикладі.
Приклад 1.2
Сума в 10 000 гр. од. покладена в банк на депозит терміном на чотири роки. Ставка по депозиту – 10% річних. Проценти по депозиту нараховуються раз в рік. Якою буде величина депозиту в кінці терміну?
За умовами даної операції відомі величини: початкова сума вкладу PV=10 000, процентна ставка r=10% і термін n=4 роки.
Визначимо майбутню величину вкладу на кінець першого періоду:
![]() .
.
Відповідно для другого періоду величина FV буде дорівнювати:
![]() .
.
Для останнього періоду (n=4):
![]() .
.
Загальне співвідношення для визначення майбутньої величини має наступний вигляд:
![]() .
(1.3)
.
(1.3)
Неважко помітити, що величина FV суттєво залежить від значень r та n. Наприклад, майбутня величина суми всього в 1,00 гр. од. при річній ставці 15% через 100 років складе 1 174 313, 45!
На рис. 1.2 наведений графік, що відображає збільшення суми в 1,00 гр. од. при різних ставках складних процентів.
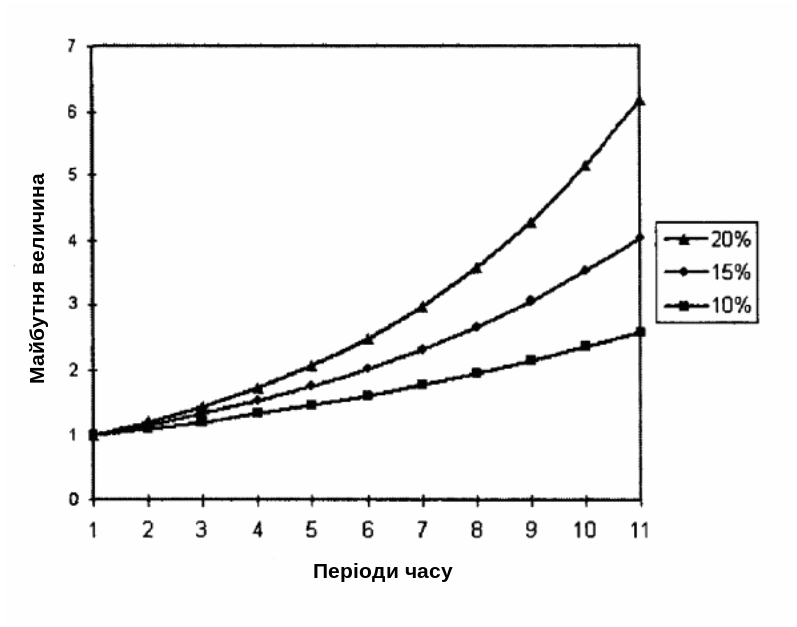 Рис.
1.2. Зростання суми в 1,00 гр. од. по ставках
складних процентів
Рис.
1.2. Зростання суми в 1,00 гр. од. по ставках
складних процентів
На практиці залежно від умов фінансової угоди проценти можуть нараховуватися декілька разів на рік, наприклад щомісячно, щоквартально і т.д. У цьому випадку співвідношення (1.3) для обчислення майбутньої вартості має вигляд:
![]() ,
(1.4)
,
(1.4)
де m – число періодів нарахування в році.
Очевидно, що чим більше m, тим швидше йде нарощення суми.
Припустимо,
що в прикладі 1.2 проценти виплачуються
щоквартально (m=4). Визначимо
![]() :
:
![]() тобто на 204,06 більше, ніж при нарахуванні
процентів раз на рік.
тобто на 204,06 більше, ніж при нарахуванні
процентів раз на рік.
Часто виникає необхідність порівняння умов фінансових операцій, що передбачають різні періоди нарахування процентів. В цьому випадку здійснюють приведення відповідних процентних ставок до їх річного еквівалента:
![]() ,
(1.5)
,
(1.5)
де r – номінальна ставка; m – число періодів нарахування.
Отриману при цьому величину називають ефективною процентною ставкою (effective percentage rate – EPR) або ставкою порівняння.
Розрахуємо ефективну процентну ставку і майбутню величину вкладу для прикладу 1.2:
![]() ;
;
![]() .
.
Таким чином, умови розміщення суми в 10 000 гр. од. на депозит терміном на 4 роки під 10% річних при щоквартальному нарахуванні процентів і під 10,3813%, що нараховуються раз нарік, є еквівалентними.
Теперішня величина елементарного потоку платежів
Формулу
для визначення теперішньої величини
елементарного потоку платежів можна
легко вивести із співвідношення (1.3)
діленням його обох частин на величину
![]() .
Виконавши відповідні математичні
перетворення, отримаємо:
.
Виконавши відповідні математичні
перетворення, отримаємо:
![]() .
(1.6)
.
(1.6)
Приклад 1.3
Виплачена по 4-річному депозиту сума склала величину в 14 641,00 гр. од. Визначити початкову величину вкладу, якщо ставка по депозиту дорівнює 10% річних.
![]() .
.
На рис. 1.3 наведений графік, що відображає процес дисконтування суми в 1,00 гр. од. при різних ставках складних процентів.

Рис. 1.3. Дисконтування суми в 1,00 при різних ставках r
Як і слід було очікувати, величина PV також залежить від тривалості операції і процентної ставки, проте залежність тут обернена – чим більші r та n, тим менша поточна (теперішня) величина.
Якщо нарахування процентів здійснюється m разів на рік, співвідношення (1.6) буде мати вигляд:
 .
(1.7)
.
(1.7)
Обчислення процентної ставки і тривалості операції
Формули для визначення величин r та n можуть бути отримані із (1.3).
При відомих величинах FV, PV та n процентну ставку можна визначити за формулою:
 .
(1.8)
.
(1.8)
Приклад 1.4
Сума в 10 000 гр. од., поміщена в банк на чотири роки, склала величину в 14 641,00 гр. од. Визначити процентну ставку (доходність операції).
![]()
Тривалість операції визначаємо шляхом логарифмування:
![]() .
(1.9)
.
(1.9)
Співвідношення (1.3) – (1.9) дозволяють визначити основні якісні характеристики фінансових операцій, в результаті здійснення яких виникають елементарні потоки платежів.
Автоматизація аналізу елементарних потоків платежів
Співвідношення (1.3) – (1.9) можуть бути легко реалізовані у вигляді відповідних формул ППП Excel. Наприклад, співвідношення (1.9), можна задати виразом:
LOG (FV / PV) / LOG (1+r),
де LOG – ім’я функції для обчислення логарифму;
FV, PV, r – відповідні числові значення.
Сучасні табличні процесори містять значну кількість готових функцій, що автоматизують проведення фінансових розрахунків. У ППП Excel для цих цілей реалізована спеціальна група із 53 функцій, що отримали назву фінансових. Для обчислення характеристик фінансових операцій з елементарними потоками платежів зручно використовувати функції БС (), КПЕР (), СТАВКА (), ПЗ () (табл. 1.1).
Таблиця 1.1
Функції для аналізу потоків платежів
Найменування функції |
Формат функції |
|
Англомовна версія |
Російськомовна версія |
|
FV |
БС |
БС(ставка;кпер;плт;пс;тип) |
NPER |
КПЕР |
КПЕР(ставка;плт;пс;бс;тип) |
RATE |
СТАВКА |
СТАВКА(кпер;плт;пс;бс;тип;предположение) |
PV |
ПС |
ПС(ставка;кпер;плт;бс;тип) |
PMT |
ПЛТ |
ПЛТ(ставка;кпер;пс;бс;тип) |
FVSСHEDULE |
БЗРАСПИС |
БЗРАСПИС (сумма; масив ставок) |
NOMINAL |
НОМИНАЛ |
НОМИНАЛ (эф_ставка; кол_пер) |
EFFECT |
ЭФФЕКТ |
ЭФФЕКТ (ном_ставка; кол_пер) |
Як видно з табл. 1.1, більшість функцій має однаковий набір базових аргументів:
ставка – процентна ставка (норма доходності або ціна позичкових коштів – r);
кпер – термін (число періодів – n) проведення операції;
плт – величина періодичного платежу (CF);
пс – початкове значення (величина PV);
бс – майбутнє значення (FV);
[тип] – тип нарахування процентів (1– початок періоду, 0 – кінець періоду), необов’язковий аргумент.
Як вище вже сказано, будь-яка із чотирьох характеристик FV, PV, r та n подібних операцій може бути визначена за відомими величинами трьох інших. Тому список аргументів кожної функції складається із трьох відомих величин (аргумент плт тут не потрібний, оскільки грошовий потік складається із єдиного платежу), при задані яких ми будемо використовувати введені вище позначення.
Для розрахунку необхідної характеристики достатньо ввести у будь-яку комірку електронної таблиці ім’я відповідної функції із заданими аргументами.
Пригадаємо, що аргументи функцій в російськомовній версії ППП Excel розділяються символом ; , а ознакою введення функції служить символ =.
Функція БС(ставка; кпер; плт; пс; тип)
Ця функція дозволяє визначити майбутнє значення потоку платежів, тобто величину FV.
Приклад 1.5
Визначити майбутню величину вкладу в 10 000 гр. од., поміщеного у банк на 5 років під 5% річних, якщо нарахування процентів здійснюється:
а) раз в рік;
б) раз у півроку;
в) раз у квартал;
г) раз у місяць.
Введіть у будь-яку комірку ЕТ:
=БС(0,05; 5; 0; -10000) (Результат: 12 762,82)
=БС(0,05/2; 5*2; 0; -10000) (Результат: 12 800,85)
=БС(0,05/4; 5*4; 0; -10000) (Результат: 12 820,37)
=БС(0,05/12; 5*12; 0; -10000) (Результат: 12 833,59)
Зверніть увагу на способи задавання аргументів.
Значення процентної ставки (аргумент ставка) зазвичай задається у вигляді десяткового дробу: 5% - 0,05; 10% - 0,1; 100% - 1 і т.д.3
Якщо нарахування процентів здійснюється m разів на рік, аргументи необхідно скоректувати відповідним чином:
![]() та
та
![]() .
.
Аргумент початкове значення – пс тут заданий у вигляді від’ємної величини (-10 000), оскільки з точки зору вкладника ця операція призводить до відтоку його грошових коштів у поточному періоді з метою отримання позитивної величини (12 762,82) через 5 років.
Проте для банку, що визначає майбутню суму повернення коштів по даному депозиту, цей аргумент повинен бути заданий у вигляді позитивної величини, так як означає надходження коштів (збільшення пасивів):
=БС(0,05; 5; 0; 10000) (Результат: -12 762,82)
Отриманий при цьому результат – від’ємна величина, оскільки операція означає витрачання коштів (повернення грошей банком вкладнику).
Як зазначалося раніше, аргумент плт не використовується при аналізі елементарних потоків, тому тут і у подальшому він має нульове значення. Його можна також задати у вигляді пустого параметра –; наприклад:
=БС(0,05; 5; ; 10000) (Результат: -12 762,82)
Особливо відзначимо, що останній аргумент функції – тип у даному випадку опущений, так як проценти у подібних операціях, як правило, нараховуються в кінці кожного періоду. У протилежному випадку функція була б задана із зазначенням всіх аргументів.
Функція КПЕР(ставка; плт; пс; бс; тип)
Функція КПЕР () обчислює кількість періодів нарахування процентів, виходячи із відомих величин r, FV та PV.
Приклад 1.6
За вкладом у 10 000 гр. од., поміщеному в банк під 5% річних, що нараховуються щорічно, була виплачена сума 12 762,82. Визначимо період проведення операції (кількість періодів нарахування).
=КПЕР(0,05; 0; -10 000; 12 762,82) (Результат: 5 років).
Відповідно при нарахуванні процентів раз у півроку, квартал, місяць число необхідних періодів буде дорівнювати:
=КПЕР(0,05/2; 0; -10 000; 12 762,82) (Результат: 10 півріч)
=КПЕР(0,05/4; 0; -10 000; 12 762,82) (Результат: 20 кварталів)
=КПЕР(0,05/12; 0; -10 000; 12 762,82) (Результат: 60 місяців)
Слід звернути особливу увагу на те, що результатом використання функції є число періодів (а не число років), необхідне для проведення операції.
Функція СТАВКА(кпер; плт; пс; бс; тип; предположение)
Функція СТАВКА () обчислює процентну ставку, котра залежно від умов операції може виступати або в якості ціни, або в якості норми її рентабельності.
Визначимо процентну ставку для прикладу 1.6.
=СТАВКА (5; 0; -10 000; 12 762,82) (Результат: 0,05 або 5%).
Результат обчислення величини r видається у вигляді періодичної процентної ставки. Для визначення річної процентної ставки отриманий результат необхідно помножити на кількість нарахувань в році.
Необхідно пам’ятати, що для отримання коректного результату при роботі функцій КПЕР () та СТАВКА () аргументи пс і бс повинні мати протилежні знаки. Дана вимога випливає з економічного змісту подібних операцій.
Наступні три функції FVSHEDULE (), NOMINAL () та EFFECT () – допоміжні. Вони призначені для зручності здійснення відповідних розрахунків.
Функція БЗРАСПИС (пс; массив ставок)
Функцію БЗРАСПИС () зручно використовувати для розрахунку майбутньої величини разової інвестиції у випадку, якщо нарахування процентів здійснюється по плаваючій ставці. Подібні операції широко розповсюджені у вітчизняній фінансовій і банківській практиці. Зокрема, доходи по облігаціях державного заощаджувального найму (ОГСЗ) нараховуються раз в квартал по плаваючій купонній ставці.
Приклад 1.7
Ставка банку по термінових валютних депозитах на початок року складає 20% річних, що нараховуються раз в квартал. Початкова сума вкладу - $1 000. Впродовж року очікується зниження ставок раз в квартал на 2, 3 та 5% відповідно. Визначити величину депозиту до кінця року.
Введемо очікувані значення процентних ставок у суміжний блок комірок електронної таблиці, наприклад: 0,2/4=0,05 – в комірку В1, 0,18/4=0,045 – в комірку В2, 0,17/4=0,0425 – в комірку В3 і 0,15/4=0,0375 – в комірку В4. Тоді функція буде мати наступний вигляд:
= БЗРАСПИС(1 000; В1:В4) (Результат: 1 186,78).
Помітьте, що величина річної ставки скорегована на кількість періодів нарахування.
Функції НОМИНАЛ (эф_ставка; кол_пер)
ЭФФЕКТ (ном_ставка; кол_пер)
Функції НОМИНАЛ ( ) та ЭФФЕКТ ( ) обчислюють відповідно номінальну та ефективну процентні ставки. Ці функції зручно використовувати при порівнянні операцій з різними періодами нарахування процентів. При цьому доходність фінансової операції зазвичай вимірюється ефективною процентною ставкою.
Приклад 1.8
Ставка банку по термінових валютних депозитах складає 18% річних. Визначимо реальну доходність вкладу (тобто ефективну ставку), якщо проценти виплачуються:
а) щомісячно
=ЭФФЕКТ (0, 18; 12) (Результат: 0,1956, або 19,56%);
б) щоквартально
=ЭФФЕКТ (0, 18; 4) (Результат: 0,1925, або 19,25%);
в) раз у півріччя
=ЭФФЕКТ (0, 18; 2) (Результат: 0,1881, або 18,81%);
г) раз у рік
=ЭФФЕКТ (0, 18; 1) (Результат: 0,18, або 18%).
Як і слід було очікувати, найбільший результат досягається при щомісячному нарахуванні процентів.
Функція НОМИНАЛ ( ) виконує обернену дію, тобто дозволяє визначити номінальну ставку за відомою величиною ефективної. Наприклад:
=НОМИНАЛ (0,1956; 12) (Результат: 0,1799 або 18%).
На рис. 1.4 наведено простий приклад шаблону, що дозволяє вирішувати типові завдання по обчисленню параметрів фінансових операцій з елементарними потоками платежів. На рис. 1.6 цей шаблон наведений у режимі відображення формул.

Рис. 1.4. Шаблон для аналізу елементарних потоків
Шаблон складається із двох частин. Перша частина займає блок комірок А2.В10 і призначена для введення вихідних даних (відомих параметрів фінансової операції). Текстова інформація у комірках А2.А10 містить найменування вихідних параметрів фінансової операції, введення яких здійснюється у комірці В6.В10. комірка В7 містить прийняте по замовчуванню число нарахувань процентів, що дорівнює 1 (тобто один раз в році). Для отримання результату необхідно ввести ще три величини.
|
А |
В |
1 |
|
|
2 |
Аналіз операцій з елементарними потоками |
|
3 |
|
|
4 |
Вихідні дані: |
|
5 |
|
|
6 |
Річна процентна ставка r = |
|
7 |
Кількість нарахувань у році m= |
1,00 |
8 |
Термін проведення операції (років) n = |
|
9 |
Початкове значення PV = |
|
10 |
Майбутнє значення FV = |
|
11 |
|
|
12 |
Результати обчислень: |
|
13 |
|
|
14 |
Майбутня величина FV = |
=БС(B6/B7;B8*B7;0;B9) |
15 |
Періодична процентна ставка r = |
=СТАВКА(B8*B7;0;B9;B10) |
16 |
Річна процентна ставка r = |
=B15*B7 |
17 |
Загальне число періодів проведення mn = |
=КПЕР(B6/B7;0;B9;B10) |
18 |
Теперішня величина PV = |
=ПС(B6/B7;B8*B7;0;B10) |
Рис. 1.5. Шаблон для аналізу елементарних потоків (формули)
Друга частина таблиці займає блок комірок А14.В18 і призначена для виведення результатів обчислень. За відсутності вихідних даних ця частина таблиці містить нульові значення в комірках В14 і В18, а також повідомлення про помилки. Блок комірок В14.В18 містить формули, необхідні для обчислення відповідних параметрів фінансової операції (рис. 1.5).
Величини r (процентна ставка) і n (термін операції) у формулах скориговані на число нарахувань процентів в році діленням і множенням на значення комірки В7 відповідно. Оскільки по замовчуванні значення комірки В7 дорівнює 1, для операцій з нарахуванням процентів раз в рік коригування параметрів r і n не буде мати жодного ефекту. При цьому тут і у подальшому розуміється задання параметра r у вигляді річної процентної ставки, а терміну здійснення операції n – в кількості років.
На рис. 1.6 наведена досконаліша версія шаблону для аналізу елементарних потоків платежів. Формули для обчислень (табл. 1.2) тут подані у вигляді логічних виразів із використанням функцій ЕСЛИ ( ), ИЛИ ( ).

Рис. 1.6. Просунутий шаблон
Таблиця 1.2
Формули шаблону
Комірка |
Формула |
В14 |
=ЕСЛИ(B6*B7*B8*B9=0;0;БС(B6/B7;B8*B7;0;B9)) |
В15 |
=ЕСЛИ(ИЛИ(B7*B8*B9*B10=0;B9*B10>=0); 0;СТАВКА(B8*B7;0;B9;B10)) |
В16 |
=B15*B7 |
В17 |
=ЕСЛИ(ИЛИ(B6*B7*B9*B10=0; B9*B10>=0);0;КПЕР(B6/B7;0;B9;B10)) |
В18 |
=ЕСЛИ(B6*B7*B8*B10=0;0;ПС(B6/B7;B8*B7;0;B10)) |
Розглянемо сенс подібного завдання на прикладі обчислення майбутньої величини (комірка В14). Логічна функція ЕСЛИ ( ) має наступний формат:
=ЕСЛИ (условие; значение_если_истина; значение_если_ложь)
Якщо параметр условие виконується (тобто умови дотримано), результатом функції буде значення виразу, задане параметром значение_если_истина, інакше – значення виразу, задане параметром значение_если_ложь.
У нашому випадку якщо виконується умова B6*B7*B8*B9=0 (тобто хоча б один необхідний для розрахунків параметр не заданий), у комірку В14 буде записаний 0 (значение_если_истина), інакше (усі параметри задані) – результат виконання функції БС(B6/B7;B8*B7;0;B9).
Таким чином, обчислення не здійснюються до тих пір, поки не будуть задані всі вихідні значення для обчислення майбутньої величини – процентна ставка (комірка В6), число нарахування процентів в році (комірка В7), кількість періодів (комірка В8) і теперішня величина (комірка В9).
Аналогічний спосіб задання формули використовується і при обчисленні теперішньої величини потоку (комірка В18).
Формули для обчислення процентної ставки (комірка В15) і числа періодів (комірка В17) містять ще одну логічну функцію – ИЛИ ( ), що має наступний формат:
=ИЛИ (логическое_значение1; логическое_значение2; …).
Результатом цієї функції є «истина», якщо виконується хоча б одна із перелічених в ній умов, і «ложь» – у протилежному випадку. Її застосування у даному випадку зумовлено необхідністю перевірки двох умов:
присутність необхідних вихідних даних (B7*B8*B9*B10=0);
наявність різних знаків у параметрів PV (комірка В9) і FV (комірка В10) – (вираз B9*B10>=0).
Подібне задання формул дозволяє уникати виникнення помилок, пов’язаних із неповнотою або некоректним заданням вихідних даних. Окрім того, таблиця при цьому більш наглядна, так як її результуюча частина завжди містить лише одне ненульове значення – величину, яку шукають.
Керуючись рис. 1.5 або рис. 1.6, підготуйте таблицю для елементарних потоків платежів і збережіть її на магнітному диску у вигляді шаблону під іменем SINGL_AN.XLT.
Приклад 1.9
Фірма «Х» пропонує взяти кредит у 100 000 гр. од. на 5 років під 12% річних. Проценти нараховуються щоквартально і підлягають виплаті разом з основною сумою боргу по завершені терміну кредиту. Визначимо суму виплати на момент погашення кредиту.
Перш за все здійснимо завантаження таблиці-шаблону.
Тепер необхідно ввести у відповідні комірки колонки В вихідні дані – величини PV, n, m, r.
Введіть 0,12 у комірку В6, 4 – у комірку В7, 5 – у комірку В8 і 100 000 – у комірку В9. Отримана таблиця повинна мати вигляд, представлений на рис. 1.7.

Рис. 1.7. Розв’язання прикладу 1.9
Розроблена таблиця-шаблон дозоляє швидко та ефективно здійснювати аналіз фінансових операцій з елементарними потоками платежів. Так, при зміні будь-якої характеристики розглянутої вище операції достатньо ввести нове значення у відповідну комірку ЕТ. Окрім того, шаблон може бути легко перетворений для одночасного аналізу відразу декількох однотипних ситуацій.
Припустимо, що фірма «Х» має альтернативну можливість отримання кредиту у 100 000 гр. од. на 5 років під 11% річних, котрі виплачуються щомісячно. Який варіант отримання кредиту вигідніший?
Для розв’язання задачі скопіюйте блок комірок В14.В18 у блок комірок С14.С18. Введіть вихідні дані альтернативного варіанту у комірки С6.С9. Отримана таблиця повинна мати вигляд, показаний на рис. 1.8.

Рис. 1.8. Аналіз двох альтернатив
Із отриманих результатів випливає, що при інших рівних умовах другий варіант отримання кредиту вигідніший.
Приклад 1.10
Корпорація «К» здійснювали виплати дивідендів своїм акціонерам впродовж 5 років. Величина дивідендів склала:
1 рік – 2,50; 2 рік – 2,60; 3 рік – 2,74; 4 рік – 2,88; 5 рік – 3,04 гр. од.
Визначити коефіцієнт зростання доходів по акціях.
Незважаючи на велику кількість вихідних даних, уважний читач легко розкриє прихований підступ і успішно розв’яже задачу, котра на перший погляд не має нічого спільного із темою, що розкривається.
Коефіцієнтом зростання у даному випадку є процентна ставка, по якій здійснюється нарощення поточної величини 2,50 до її майбутнього значення 3,04 за 4 роки. Таким чином задача зводиться до обчислення ставки r при відомих величинах FV, PV, n.
Введіть вихідні дані у шаблон (не забувайте, що величини PVта FVповинні мати різні знаки!). Отримана таблиця повинна мати майбутній вигляд (рис. 1.9).

Рис. 1.9. Розв’язання прикладу 1.10
Протестуйте розроблений шаблон на розв’язанні прикладів 1.2 – 1.8 і порівняйте отримані результати з наведеними.
