3 Ітерація циклу. Знаходимо у виділеній частині ребро з мінімальною вагою серед ребер з різнокольровими вершинами.

	1	2	3	4	5
1	0	3	5	2	7
2	3	0	3	7	5
3	5	3	0	10	4
4	2	7	10	0	4
5	7	5	4	4	0

Рисунок 13

Це ребро (2, 3), вага якого дорівнює 3. Зберігаємо назву ребра.

Позначаємо вузли 1 та 2 однаковим кольором.

Вершина	1	2	3	4	5
Колір	1	1	1	1	5

Рисунок 14

4 Ітерація циклу. Знаходимо у виділеній частині ребро з мінімальною вагою серед ребер з різнокольровими вершинами.

	1	2	3	4	5
1	0	3	5	2	7
2	3	0	3	7	5
3	5	3	0	10	4
4	2	7	10	0	4
5	7	5	4	4	0

Рисунок 15

Це ребро (3, 5), вага якого дорівнює 4. Зберігаємо назву ребра.

Позначаємо вузли 1 та 2 однаковим кольором.

Вершина	1	2	3	4	5
Колір	1	1	1	1	1

Рисунок 16

Тепер всі вузли графа розфарбовані в однаковий колір, тобто виконана умова виходу з циклу.

Після виконання циклу ми одержали наступний список ребер: (1, 4), (1, 2), (2, 3), (3, 5), на основі нього будуємо каркасне дерево зображене на рисунку 17.

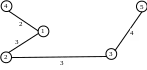
Рисунок 17 – Мінімальне каркасне дерево для графу з рисунку 2, його сумарна вага дорівнює 12

Результат: Оптоволоконну лінію потрібно провести між наступними парами сіл (1, 4), (1, 2), (2, 3), (3, 5). Необхідна довжина дроту рівна 12 умовним одиницям відстані.