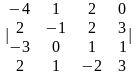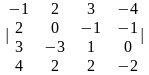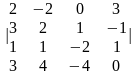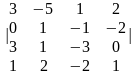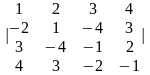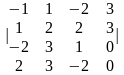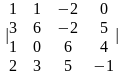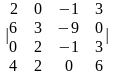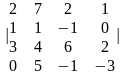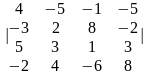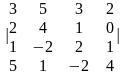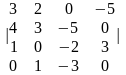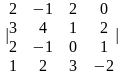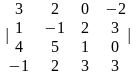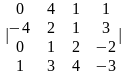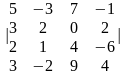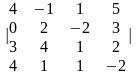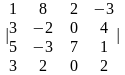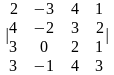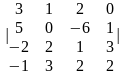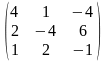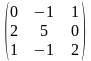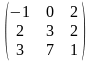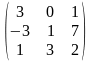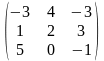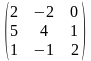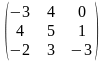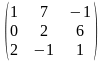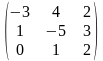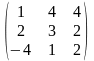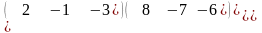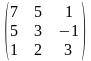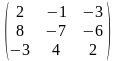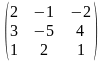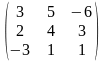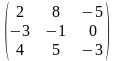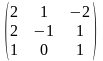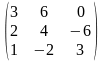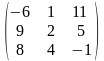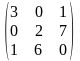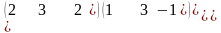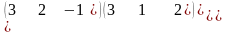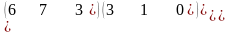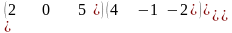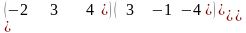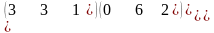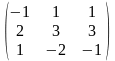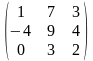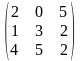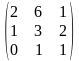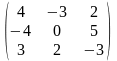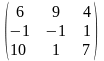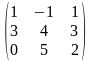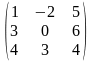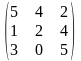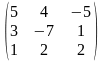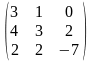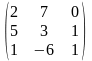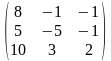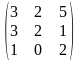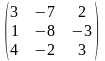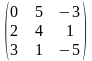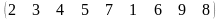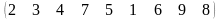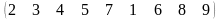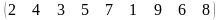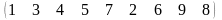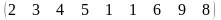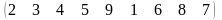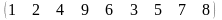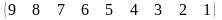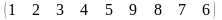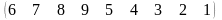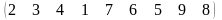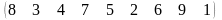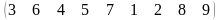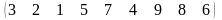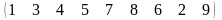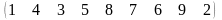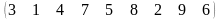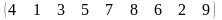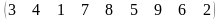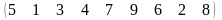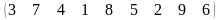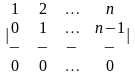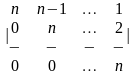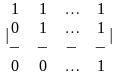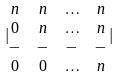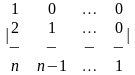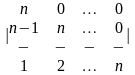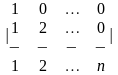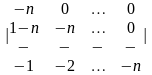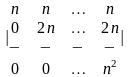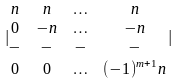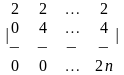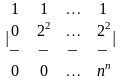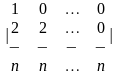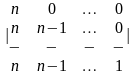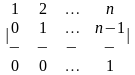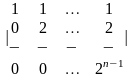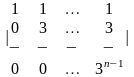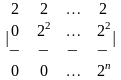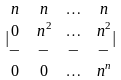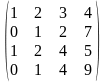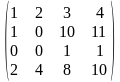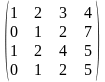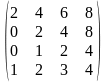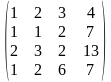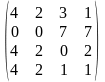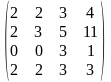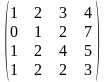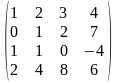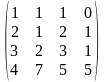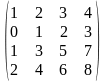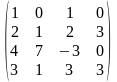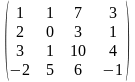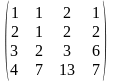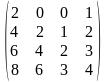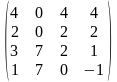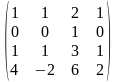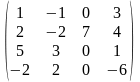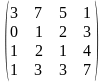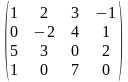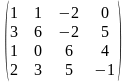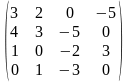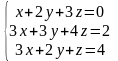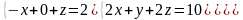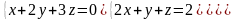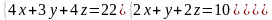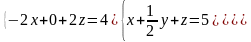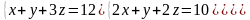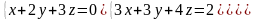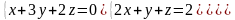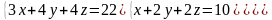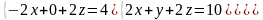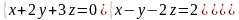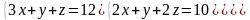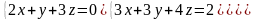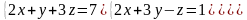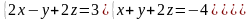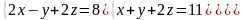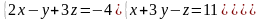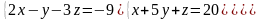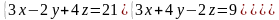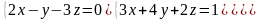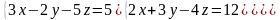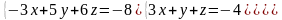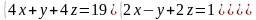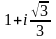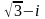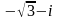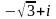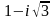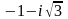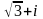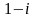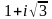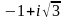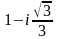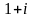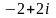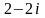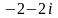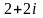- •Қазақстан республикасы бiлiм және ғылым министрлiгi
- •Кафедра «Математиканы оқытудың теориясы мен әдістемесі» Нурмаганбетова ж.А., Мадияров н.К.
- •«Алгебра және сандар теориясы» пәнінен
- •Шымкент-2013
- •Теориялық сұрақтар
- •Жеке жұмыс тапсырмалары
- •«Алгебра және сандар теориясы» пәні бойынша рефераттар тақырыптарының тізімі
- •Баллды-рейтингті жүйе бойынша студенттердің өзіндік жұмыстарын бағалау өлшемі
- •Әдебиеттер
- •Әдiстемелiк нұсқау
Жеке жұмыс тапсырмалары
1-ТАПСЫРМА. Берiлген анықтауышты есептеңдер.
а) қатарының немесе бағанының элементтерi бойынша жiктеу арқылы;
ә) алдын-ала қатарының немесе бағанының элементтерiн нольге айналдыру арқылы;
б) анықтауышты үшбұрышты түрге келтiру арқылы.
1.1 |
|
1.2 |
|
1.3 |
|
|
|
|
|
|
|
1.4 |
|
1.5 |
|
1.6 |
|
|
|
|
|
|
|
1.7 |
|
1.8 |
|
1.9 |
|
|
|
|
|
|
|
1.10 |
|
1.11 |
|
1.12 |
|
|
|
|
|
|
|
1.13 |
|
1.14 |
|
1.15 |
|
|
|
|
|
|
|
1.16 |
|
1.17 |
|
1.18 |
|
|
|
|
|
|
|
1.19 |
|
1.20 |
|
1.21 |
|
|
|
|
|
|
|
1.22 |
|
1.23 |
|
1.24 |
|
|
|
|
|
|
|
1.25 |
|
|
|
|
|
2-ТАПСЫРМА.
А және В матритцалары берiлген.
Табу керек: а)АВ ә)ВА б)
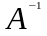 в)
в)
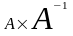
2.1 |
|
А= |
|
В= |
|
|
|
|
|
2.2 |
|
А= |
|
В= |
|
|
|
|
|
2.3 |
|
А= |
|
В= |
|
|
|
|
|
2.4 |
|
А= |
|
В= |
|
|
|
|
|
2.5 |
|
А= |
|
В= |
|
|
|
|
|
2.6 |
|
А= |
|
В= |
|
|
|
|
|
2.7 |
|
А= |
|
В= |
|
|
|
|
|
2.8 |
|
А= |
|
В= |
|
|
|
|
|
2.9 |
|
А= |
|
В= |
|
|
|
|
|
2.10 |
|
А= |
|
В= |
|
|
|
|
|
2.11 |
|
А= |
|
В= |
|
|
|
|
|
2.12 |
|
А= |
|
В= |
|
|
|
|
|
2.13 |
|
А= |
|
В= |
|
|
|
|
|
2.14 |
|
А= |
|
В= |
2.15 |
|
А= |
|
В= |
|
|
|
|
|
2.16 |
|
А= |
|
В= |
|
|
|
|
|
2.17 |
|
А= |
|
В= |
|
|
|
|
|
2.18 |
|
А= |
|
В= |
|
|
|
|
|
2.19 |
|
А= |
|
В= |
|
|
|
|
|
2.20 |
|
А= |
|
В= |
|
|
|
|
|
2.21 |
|
А= |
|
В= |
|
|
|
|
|
2.22 |
|
А= |
|
В= |
|
|
|
|
|
2.23 |
|
А= |
|
В= |
|
|
|
|
|
2.24 |
|
А= |
|
В= |
|
|
|
|
|
2.25 |
|
А= |
|
В= |
3 - ТАПСЫРМА. Ауыстырудың инверсиялар санын анықтаңдар .
3.1 |
|
3.2 |
|
|
|
|
|
3.3 |
|
3.4 |
|
|
|
|
|
3.5 |
|
3.6 |
|
|
|
|
|
3.7 |
|
3.8 |
|
|
|
|
|
3.9 |
|
3.10 |
|
|
|
|
|
3.11 |
|
3.12 |
|
|
|
|
|
3.13 |
|
3.14 |
|
|
|
|
|
3.15 |
|
3.16 |
|
|
|
|
|
3.17 |
|
3.18 |
|
|
|
|
|
3.19 |
|
3.20 |
|
|
|
|
|
3.21 |
|
3.22 |
|
|
|
|
|
3.23 |
|
3.24 |
|
|
|
|
|
3.25 |
|
|
|
4 - ТАПСЫРМА. Анықтауышты есептеңiз және аij элементiнiң жалпы түрiн анықтаңыз .
4.1 |
|
4.2 |
|
4.3 |
|
|
|
|
|
|
|
4.4 |
|
4.5 |
|
4.6 |
|
|
|
|
|
|
|
4.7 |
|
4.8 |
|
4.9 |
|
|
|
|
|
|
|
4.10 |
|
4.11 |
|
4.12 |
|
|
|
|
|
|
|
4.13 |
|
4.14 |
|
4.15 |
|
|
|
|
|
|
|
4.16 |
|
4.17 |
|
4.18 |
|
|
|
|
|
|
|
4.19 |
|
4.20 |
|
4.21 |
|
|
|
|
|
|
|
4.22 |
|
4.23 |
|
4.24 |
|
|
|
|
|
|
|
4.25 |
|
|
|
|
|
5 - ТАПСЫРМА. Матрицаның рангiн есептеңдер.
а) Жиектеушi минорлар әдiсiмен;
б) Элементар түрлендiру арқылы.
5.1 |
|
5.2 |
|
5.3 |
|
|
|
|
|
|
|
5.4 |
|
5.5 |
|
5.6 |
|
|
|
|
|
|
|
5.7 |
|
5.8 |
|
5.9 |
|
|
|
|
|
|
|
5.10 |
|
5.11 |
|
5.12 |
|
|
|
|
|
|
|
5.13 |
|
5.14 |
|
5.15 |
|
|
|
|
|
|
|
5.16 |
|
5.17 |
|
5.18 |
|
|
|
|
|
|
|
5.19 |
|
5.20 |
|
5.21 |
|
|
|
|
|
|
|
5.22 |
|
5.23 |
|
5.24 |
|
|
|
|
|
|
|
5.25 |
|
|
|
|
|
6 - ТАПСЫРМА. Крамер, Гаусс және матрицалық есептеу ережелерiн
қолданып жүйенi шешiңдер.
6.1 |
|
6.2 |
|
6.3 |
|
|
|
|
|
|
|
6.4 |
|
6.5 |
|
6.6 |
|
|
|
|
|
|
|
6.7 |
|
6.8 |
|
6.9 |
|
|
|
|
|
|
|
6.10 |
|
6.11 |
|
6.12 |
|
|
|
|
|
|
|
6.13 |
|
6.14 |
|
6.15 |
|
|
|
|
|
|
|
6.16 |
|
6.17 |
|
6.18 |
|
|
|
|
|
|
|
6.19 |
|
6.20 |
|
6.21 |
|
|
|
|
|
|
|
6.22 |
|
6.23 |
|
6.24 |
|
|
|
|
|
|
|
6.25 |
|
|
|
|
|
7 - ТАПСЫРМА. Бiртектi сызықты теңдеулер жүйесiн шешiп, оның iргелi шешiмiн табыңдар.
7.1.
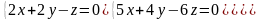 7.2.
7.2.
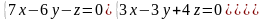 7.3.
7.3.
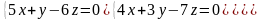
7.4.
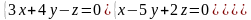 7.5.
7.5.
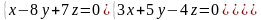 7.6.
7.6.
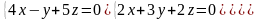
7.7.
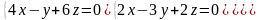 7.8.
7.8.
 7.9.
7.9.
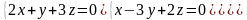
7.10.
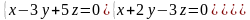 7.11.
7.11.
 7.12.
7.12.
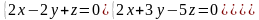
7.13.
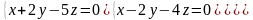 7.14.
7.14.
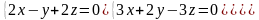 7.15.
7.15.
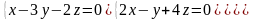
7.16.
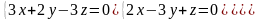 7.17.
7.17.
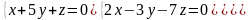 7.18.
7.18.
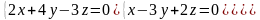
7.19.
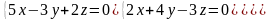 7.20.
7.20.
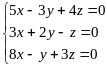 7.21.
7.21.
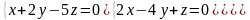
7.22.
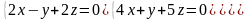 7.23.
7.23.
 7.24.
7.24.
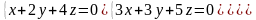
7.25.

8-ТАПСЫРМА. Берiлген векторлар жүйесiн ортогоналдаңдар
8.1 |
(2,3,5), (4,1,2) |
8.2 |
(7.2,4), (3,2,5) |
8.3 |
(1,2,1), (3,4,2) |
|
|
|
|
|
|
8.4 |
(3,-1,-2), (1,4,7) |
8.5 |
(3,-2,3), (2,4,1) |
8.6 |
(1,2,1), (3,4,2) |
|
|
|
|
|
|
8.7 |
(1,-1,1), (2,3,1) |
8.8 |
(1,1,1), (2,-1,0) |
8.9 |
(2,1,0), (3,1,2) |
|
|
|
|
|
|
8.10 |
(1,4,-1), (3,2,0) |
8.11 |
(1,0,1), (2,1,-1) |
8.12 |
(2,-2,-2), (0,3,-6) |
|
|
|
|
|
|
8.13 |
(1,2,1), (-4,1,5) |
8.14 |
(2,-1,-2), (1,3,1) |
8.15 |
(6,5,-1), (0,3,-6) |
|
|
|
|
|
|
8.16 |
(3,1,2), (4,0,-1) |
8.17 |
(5,-2,-16), (0,3,-6) |
8.18 |
(2,-2,-2), (1,3,6) |
|
|
|
|
|
|
8.19 |
(1,1,2), (4,0,-1) |
8.20 |
(1,5,3), (1,3,-1) |
8.21 |
(1,-2,10), (2,-4,-1) |
|
|
|
|
|
|
8.22 |
(4,2,3), (2,-1,-2) |
8.23 |
(-7,2,1), (-4,1,5) |
8.24 |
(5,-2,-1), (5,3,-6) |
|
|
|
|
|
|
8.25 |
(3,1,2), (4,2,-1) |
|
|
|
|
9-ТАПСЫРМА. S базисiнен S/ базисiне көшу матрицасын табыңыз.
9.1 |
S=((1,2,0), (1,1,1),(0,2,1)), S/= ((5,-6,-2), (-1,6,1), (2,6,7)) |
9.2 |
S=((1,0,0), (0,1,0),(0,0,1)), S/= ((1,1,0), (0,1,1), (1,0,1)) |
|
|
|
|
9.3 |
S=((1,3,2,), (2,2,-1),(-3,-4,0)), S/= ((1,10,10), (-3,2,7), (0,7,8)) |
9.4 |
S=((1,2,2,), (2,1,-4),(3,-4,2)), S/= ((1,4,5), (-1,3,7), (2,7,8)) |
9.5 |
S=((2,3,1,), (1,2,-1),(3,-4,5)), S/= ((1,10,10), (-3,2,7), (0,7,8) |
9.6 |
S=((1,2,6,), (1,2,-1),(7,4,1)), S/= ((1,-5,9), (1,3,7), (5,7,1)) |
|
|
|
|
9.7 |
S=((1,1,2,), (2,2,7),(3,-1,4)), S/= ((2,6,1), (5,2,3), (6,7,8) |
9.8 |
S=((1,3,-2,), (-2,2,-1),(3,-4,5)), S/= ((1,1,-2), (3,-2,7), (2,0,8)) |
|
|
|
|
9.9 |
S=((1,-1,2,), (5,2,1),(3,8,0)), S/= ((2,1,-1), (3,-2,7), (3,-1,8)) |
9.10 |
S=((1,-3,2,), (-2,0,-1),(3,-4,0)), S/= ((1,11,-1), (3,0,7), (3,1,4)) |
|
|
|
|
9.11 |
S=((1,0,2,), (0,2,-1),(3,-4,0)), S/= ((1,0,11), (-3,4,7), (1,7,8)) |
9.12 |
S=((1,7,4,), (1,2,1),(4,-4,2)), S/= ((1,1,7), (3,0,5), (0,1,3)) |
|
|
|
|
9.13 |
S=((1,1,-2,), (8,2,-1),(3,-1,1)), S/= ((2,7,3), (2,-2,5), (1,3,2)) |
9.14 |
S=((1,-3,-2,), (-2,-2,-1),(3,4,1)), S/= ((1,-3,-4), (3,-2,-1), (1,2,3)) |
|
|
|
|
9.15 |
S=((1,5,-2,), (2,2,-1),(2,3,10)), S/= ((2,3,3), (-1,3,5), (1,3,2)) |
9.16 |
S=((1,9,1,), (1,2,1),(3,-2,)), S/= ((1,5,10), (-1,4,3), (1,7,2)) |
|
|
|
|
9.17 |
S=((1,-3,2,), (-2,2,-1),(-3,-4,1)), S/= ((1,0,1), (3,2,1), (1,7,1)) |
9.18 |
S=((1,2,2,), (2,2,-2),(-3,-3,3)), S/= ((1,1,0), (-2,2,1), (1,3,1)) |
|
|
|
|
9.19 |
S=((1,-1,-2,), (-1,2,1),(-3,4,1)), S/= ((1,-2, 6), (-3,2,7), (0,7,8)) |
9.20 |
S=((1,3,2,), (2,2,-1),(-3,-4,0)), S/= ((1,1,0), (-1,2,3), (2,1,3)) |
|
|
|
|
9.21 |
S=((1,-1,-2,), (12,2,-1),(3,-4,1)), S/= ((1,1,1), (-5,2,2), (1,3,3)) |
9.22 |
S=((1,0,2,), (0,2,-1),(-3,4,0)), S/= ((1,1,-1), (3,2,3), (2,3,5)) |
|
|
|
|
9.23 |
S=((1,-2,2,), (0,2,-1),(0,-2,1)), S/= ((1,10,10), (-3,2,7), (0,7,8)) |
9.24 |
S=((1,-2,1,), (1,2,-1),(-2,-1,2)), S/= ((1,3,0), (2,-2,1), (1,-3,2)) |
|
|
|
|
9.25 |
S=((1,0,2,), (0,2,-1),(3,4,0)), S/= ((1,0,1), (0,2,1), (0,7,1)) |
|
|
10-ТАПСЫРМА. Сызықты түрлендiрудiң меншiктi мәндерiн және меншікті векторын табыңдар:
10.1 |
|
10.2 |
|
10.3 |
|
|
|
|
|
|
|
10.4 |
|
10.5 |
|
10.6 |
|
|
|
|
|
|
|
10.7 |
|
10.8 |
|
10.9 |
|
|
|
|
|
|
|
10.10 |
|
10.11 |
|
10.12 |
|
|
|
|
|
|
|
10.13 |
|
10.14 |
|
10.15 |
|
|
|
|
|
|
|
10.16 |
|
10.17 |
|
10.18 |
|
|
|
|
|
|
|
10.19 |
|
10.20 |
|
10.21 |
|
|
|
|
|
|
|
10.22 |
|
10.23 |
|
10.24 |
|
|
|
|
|
|
|
10.25 |
|
|
|
|
|
11-ТАПСЫРМА. Берілген cанды комплекс жазықтықта бейнелеп, оны алгебралық, тригонометриялық және көрсеткiштiк түрде жазып және есептеп, бейнесiн табу керек.
|
|
|
|