
- •Б.Т. Добрица, и.В. Дубограй, о.В. Скуднева. Кратные интегралы и их приложения. Электронное учебное издание
- •Добрица Борис Тимофеевич Дубограй Ирина Валерьевна Скуднева Оксана Валентиновна.
- •Введение.
- •Модуль 1.
- •1.Определение двойного интеграла. Теорема о его существовании.
- •2. Свойства двойного интеграла.
- •3.Геометрический смысл двойного интеграла.
- •4. Повторный интеграл.
- •5. Переход от двойного интеграла к повторному. Расстановка пределов интегрирования.
- •1.Замена переменных в двойном интеграле.
- •2.Геометрический смысл модуля и знака Якобиана.
- •4.Обобщённые полярные координаты.
- •1.Вычисление объемов тел с помощью двойного интеграла.
- •2.Вычисление площади поверхности. Понятие площади поверхности.
- •1. Вычисление массы материальной пластинки.
- •1.Определение тройного интеграла.
- •2.Теорема существования тройного интеграла.
- •3.Свойства тройного интеграла.
- •6. Интеграл от единичной функции по области равен объёму этой области.
- •3.Сферическая система координат.
- •2. Несобственный двойной интеграл первого рода ( по неограниченной области). Интеграл Пуассона.
- •Пример аттестационного билета.
- •Приложения.
- •Типовой расчёт №1 «Кратные интегралы».
- •Задача 5.
- •Задача 6.
- •Дополнительная литература
- •Методические пособия, Кафедральные издания и методические материалы
4. Повторный интеграл.
Повторным
называется двойной интеграл вида
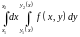 (1.4а)
или
(1.4а)
или
 (1.4б).
(1.4б).
При
вычислении первого из указанных повторных
интегралов сначала берётся внутренний
интеграл
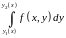 по переменной
по переменной
 ,
при этом
,
при этом
 играет роль параметра. Затем полученную
функцию интегрируют по переменной x.
играет роль параметра. Затем полученную
функцию интегрируют по переменной x.
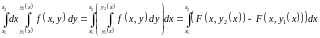 ,
где
,
где
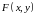 -
первообразная функции
-
первообразная функции
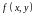 по
,
т.е.
по
,
т.е.
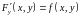 .
.
Аналогично,
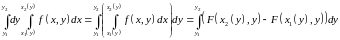 ,
где
,
где
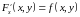 .
.
Пример1.2.
Вычислить повторный интеграл :
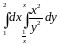 .
.
Решение.
Вычислим
сначала внутренний интеграл, при этом
множитель
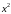 ,
играющий роль параметра (не зависящего
от переменной интегрирования), вынесем
за знак этого интеграла.
,
играющий роль параметра (не зависящего
от переменной интегрирования), вынесем
за знак этого интеграла.
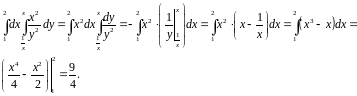
5. Переход от двойного интеграла к повторному. Расстановка пределов интегрирования.
Д
Рисунок 1.4
ля вычисления значения двойного интеграла (1.1) необходимо перейти к повторному интегралу вида (1.4а) или (1.4б) . Способ перехода зависит от вида области D.Область, ограниченная слева и справа прямыми
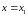 и
и
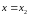 ,
,
а
сверху и снизу - кривыми
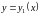 и
и
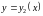 ,
такими, что любая прямая
,
такими, что любая прямая
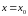
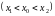 ,
проведённая через область D,
пересекает каждую из кривых
и
в одной точке, называется
,
проведённая через область D,
пересекает каждую из кривых
и
в одной точке, называется
y-правильной. При этом точку А называют точкой входа в область, а точку В – точкой выхода из области.
(см.рис
1.4) То есть область
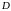 является y-правильной,
если
является y-правильной,
если
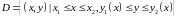
О пределив
пределы изменения переменных по области
D,
расставляем пределы интегрирования в
повторном интеграле:
пределив
пределы изменения переменных по области
D,
расставляем пределы интегрирования в
повторном интеграле:
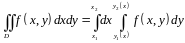 . (1.4а)
. (1.4а)
А
Рисунок 1.5
налогично вводится понятие x-правильной области (см. рис. 1.5).В
этом случае имеем
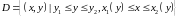 и
и
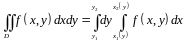 (1.4б)
(1.4б)
Пример
1.3. Расставить
двумя способами пределы интегирования
в двойном интеграле
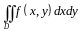 ,
где
D
– треугольник с вершинами O(0,0),
A(0,1),В(1,1).
,
где
D
– треугольник с вершинами O(0,0),
A(0,1),В(1,1).
Решение. Построим область D. Она одновременно является как
 y-правильной,
так и
x-правильной.
Поэтому
первый способ расстановки пределов при
переходе к повторному интегралу выглядит
следующим образом:
y-правильной,
так и
x-правильной.
Поэтому
первый способ расстановки пределов при
переходе к повторному интегралу выглядит
следующим образом:
для
всех точек данной области переменная
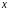 изменяется
между
изменяется
между
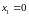 и
и
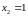 ,
а переменная
,
а переменная
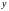 для
любого из этих
меняется от
для
любого из этих
меняется от
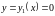 до
до
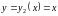 ,
т.е..
,
т.е..
Рис. 1.6
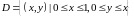 .
Определив
пределы изменения переменных по области
D,
расставляем пределы интегрирования в
повторном интеграле:
.
Определив
пределы изменения переменных по области
D,
расставляем пределы интегрирования в
повторном интеграле:

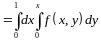 .
(См.(1.4а))
.
(См.(1.4а))
Изменим порядок интегрирования, то есть расставим пределы интегрирования в повторном интеграле вторым способом (См.(1.4б)).
Из
рис. 1.6 следует, что для всех точек данной
области переменная
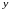 изменяется
между
изменяется
между
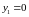 и
и
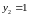 ,
а переменная
,
а переменная
 для
любого из этих
меняется от
для
любого из этих
меняется от
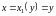 до
до
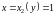 .
Т.е.
.
Т.е.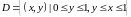 Теперь
расставляем пределы интегрирования:
Теперь
расставляем пределы интегрирования:
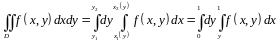 .
.
Пример
1.4. Изменить
порядок интегрирования в повторном
интеграле
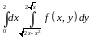 .
.
Решение.
Из данного интеграла следует, что область
интегрирования ограничена прямыми
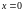 ,
,
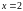 и кривыми
и кривыми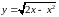 ,
,
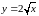 .
.
 Построим область D
(См. рис. 1.7).
Она является
y-правильной,
но не является x-правильной
(См. рис
.1.4). Для
получения x-правильных
областей
придётся разбить область D
на три части.
Определим пределы, в которых меняются
переменные по каждой из трёх областей
для повторных интегралов вида (1.4б).
Построим область D
(См. рис. 1.7).
Она является
y-правильной,
но не является x-правильной
(См. рис
.1.4). Для
получения x-правильных
областей
придётся разбить область D
на три части.
Определим пределы, в которых меняются
переменные по каждой из трёх областей
для повторных интегралов вида (1.4б).
Рис.
1.7
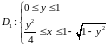 ,
,
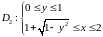
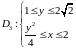
По свойству аддитивности имеем
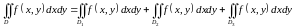 . Переходя к
повторным интегралам вида (1.4б),
расставляем пределы интегрирования в
каждом из трёх слагаемых и получаем
ответ:
. Переходя к
повторным интегралам вида (1.4б),
расставляем пределы интегрирования в
каждом из трёх слагаемых и получаем
ответ:
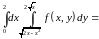
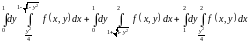 .
.
Пример
1.5. Вычислим
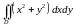 ,
где область
,
где область
 ограничена линий
ограничена линий
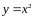 и
и
 .
.
Решение.
Линии,
задающие область
,
пересекаются в точках с абсциссами
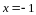
и
Рис. 1.8
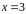 . Построим область
и
выясним, является ли она правильной
(См. рис.1.8). Сравнив данную область с
областями, представленными на рис. 1.3 и
рис. 1.4, видим, что наша область является
y-правильной,
но не является x
–правильной.
. Построим область
и
выясним, является ли она правильной
(См. рис.1.8). Сравнив данную область с
областями, представленными на рис. 1.3 и
рис. 1.4, видим, что наша область является
y-правильной,
но не является x
–правильной.
Перейдём от двойного интеграла к повторному вида (1.4а) и вычислим его.
Учтём, что по области D переменные меняются в следующих пределах:
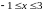 и
и
 .
.
Расставим
пределы интегрирования и вычислим
интеграл.
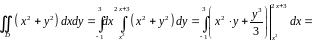

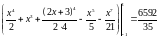
Проверка решения в среде MathCad.
Для
того чтобы вычислить двойной интеграл
с помощью компьютерной математической
программы MathCad,
необходимо сначала представить двойной
интеграл в виде повторного. Для записи
задания откроем панели инструментов
«Калькулятор», «Математический анализ»
и «Вычисления». На панели «Математический
анализ» находим значок определённого
интеграла и нажимаем на него два раза.
Двойной интеграл строится по принципу
вложения. Над тем интегралом, что окажется
левее («внешним»), ставим числовые
пределы интегрирования – в нашем примере
это значения переменной
и
.
Над следующим интегралом («внутренним»)
ставим функциональные пределы,
ограничивающие область
по переменной y.
В нашем примере это
и
.
Далее записываем подынтегральную
функцию x2+y2
и dydx.
То есть первой указывается та переменная,
по которой сначала ведётся интегрирование
(y)
. Если после записи интеграла поставить
знак «равно» с панели «Калькулятор»
или «Вычисления», программа выдаст
приблизительное числовое значение
вычисляемого интеграла в виде десятичной
дроби. Если же на панели «Вычисления»
выбрать и поставить после интеграла
значок «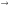 »,
компьютер выведет результат вычисления
в аналитической записи, в виде простой
дроби или выражения, содержащего корни,
числа e,
»,
компьютер выведет результат вычисления
в аналитической записи, в виде простой
дроби или выражения, содержащего корни,
числа e,
 и проч.
и проч.
На рисунке 11 представлен «принтскрин» с экрана при решении данного примера.
Рис. 11
Домашнее задание к занятию 1: ОЛ-6 №№2115, 2117, 2122, 2124,2144, 2146 или ОЛ-5 №№ 8.4, 7, 10, 14, 21, 32, 34.
Занятие 2
Криволинейные координаты на плоскости. Замена переменных в двойном интеграле. Геометрический смысл модуля и знака Якобиана. Двойной интеграл в полярных координатах. Вычисление площади плоской фигуры с помощью двойного интеграла.
Ауд.: ОЛ-6 №№ 2160, 2162, 2164, 2166, 2171, 2177, 2183 или ОЛ-5 №№ 8.43, 44, 46, 48, 50, 56, 62.
