4. Вычисление объемов тел вращения

Рассмотрим кривую, заданную уравнением . Предположим, что функция непрерывна на отрезке . Если соответствующую ей криволинейную трапецию с основаниями и вращать вокруг оси Ох, то получим так называемое тело вращения.

Каждое сечение тела плоскостью представляет собой круг радиуса . Следовательно, объем тела вращения находится по полученной выше формуле:

5. Вычисление площадей поверхности тела вращения

Определение. Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Разобьем дугу АВ на n частей точками . Координаты вершин полученной ломаной имеют координаты и . При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна . Эта площадь может быть найдена по формуле:

Здесь – длина каждой хорды. Следовательно,

Применяя теорему Лагранжа к отношению , получим:

Тогда ,

Площадь поверхности, описанной ломаной равна:

Эта сумма не является интегральной, но можно показать, что

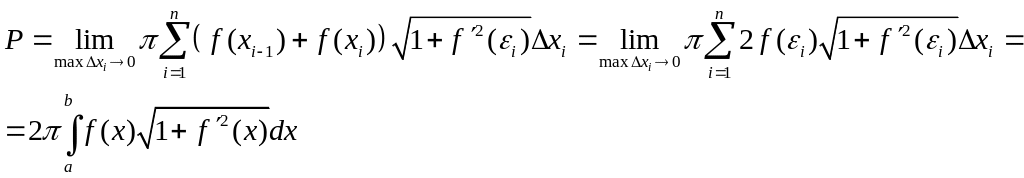Получаем формулу вычисления площади поверхности тела вращения.

5.4 Несобственные интегралы и методы их вычисления

1. Понятие несобственного интеграла

Пусть функция определена и непрерывна на интервале . Тогда она непрерывна и, следовательно, интегрируема на любом конечном отрезке .

Определение. Предел называется несобственным интегралом от функции на интервале .

Обозначение:

Определение. Если этот предел существует и конечен, то говорят, что несобственный интеграл называется сходящимся. Если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.

Аналогичные рассуждения можно привести для несобственных интегралов вида: