1. Оценим точность построенных моделей на основе средней ошибки аппроксимации: %, сведя все вычисления в табл. 2.

Таблица 2. Промежуточные данные расчета моделей

Месяцы
1	3433	150	147,85	144,83	141,72
2	3436	150	148,09	145,05	142,03
3	3449	140	149,13	146,00	143,34
4	3504	130	153,53	150,06	148,76
5	3693	165	168,65	164,37	166,18
6	3850	190	181,21	176,68	179,34
7	4312	215	218,17	215,05	212,52
8	4341	198	220,49	217,56	214,37
9	4354	220	221,53	218,69	215,19
10	4425	225	227,21	224,91	219,58
Итого:		1783	1835,86	1803,21	1783,02

Месяцы
1	3433	150	1,4333	3,4467	5,5170
2	3436	150	1,2733	3,3003	5,3149
3	3449	140	6,5214	4,2874	2,3825
4	3504	130	18,1000	15,4332	14,4320
5	3693	165	2,2121	0,3788	0,7123
6	3850	190	4,6263	7,0102	5,6102
7	4312	215	1,4744	0,0218	1,1532
8	4341	198	11,3586	9,8792	8,2665
9	4354	220	0,6955	0,5946	2,1874
10	4425	225	0,9822	0,0389	2,4082
Итого:		1783	48,6772	44,3912	47,9843

Тогда имеем следующие значения для средней относительной ошибки:

- для линейной модели , т.е. в среднем расчетные значения для этой модели отличаются от фактических значений на 4,87%, что говорит о высокой точности уравнения регрессии (ошибка аппроксимации в 5-7% свидетельствует о хорошем подборе модели к исходным данным).

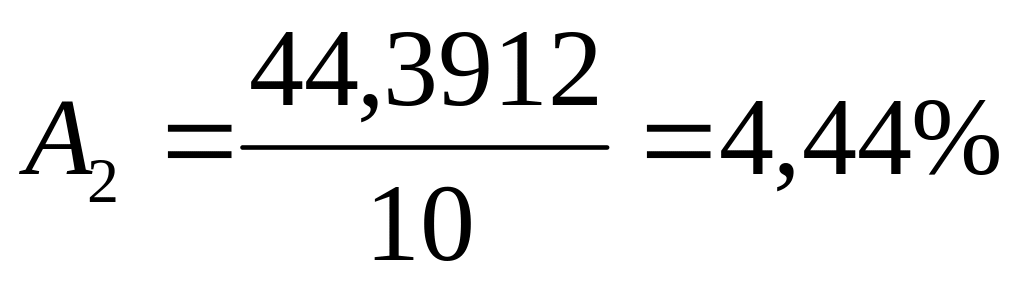• , т.е. в среднем расчетные значения для степенной модели отличаются от фактических значений на 4,44%, что говорит о хорошем качестве уравнения регрессии;

• , т.е. в среднем расчетные значения для гиперболической модели отличаются от фактических значений на 4,80%, что говорит о хорошем качестве уравнения регрессии. Так как меньшей ошибкой аппроксимации обладает степенная модель, по этому показателю она наилучшая.

Сделаем прогноз на 2 шага вперед по гиперболической модели . Для этого необходимо сначала рассчитать прогнозные точечные значения переменной х на два шага вперед. Воспользуемся встроенными функциями Excel, построим диаграмму и добавим линию тренда.

Рис. 1. График фактических и модельных значений

Таким образом, найдем прогнозные значения переменной х:

;

Прогнозные значения переменной у:

; .

Найдем верхнюю и нижнюю границу прогноза:

где .

Получаем: ; и , тогда

. .

Точечный прогноз у	Интервальные оценки прогноза
	Нижняя граница	Верхняя граница
231,30	204,418	258,184
238,65	207,937	269,357

Построим графики фактических и прогнозных модельных значений:

Рис. Графики прогноза

111