III. Задачи для упражнений

1. Вычислите методом окаймления миноров ранги указанных матриц:

а) ; б) .

2. Вычислите ранг матриц с помощью элементарных перобразований:

а) ; б) .

3. Исследуйте, совместны ли системы линейных уравнений, решите их:

а) 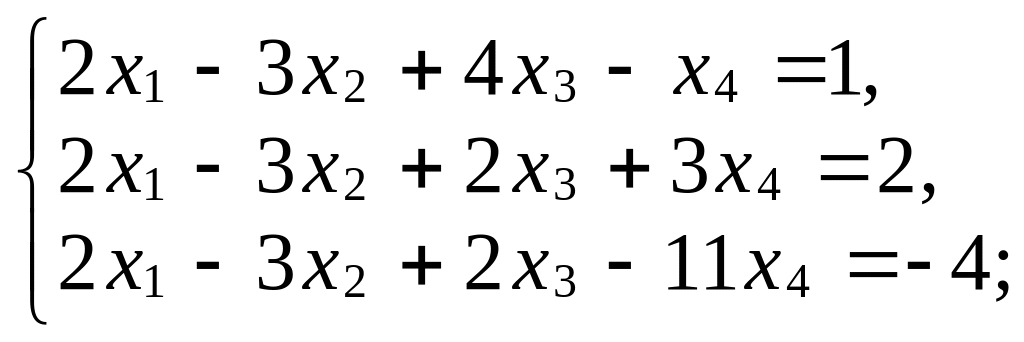б)

в)

IV. Задачи для самостоятельного решения

1. Найдите ранг матриц: а) ; б) .

2. Исследуйте, совместны ли системы линейных уравнений, решите их:

а) 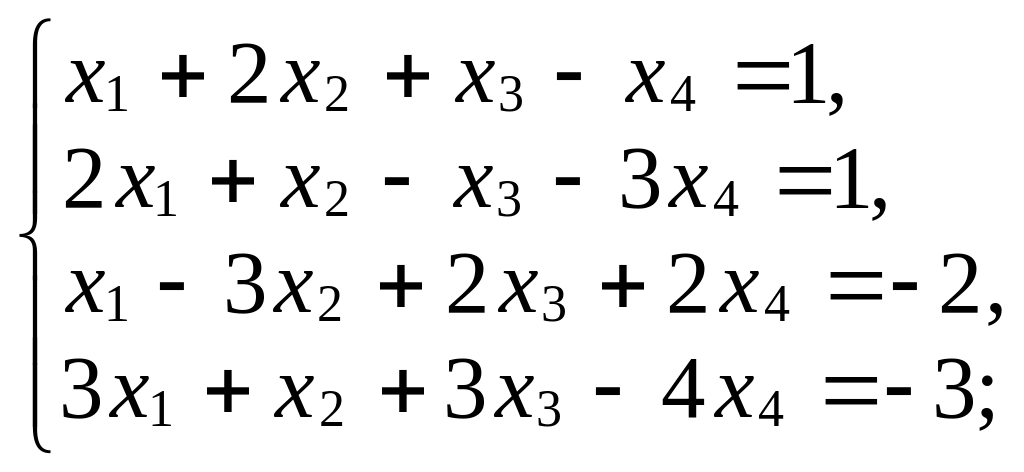б)

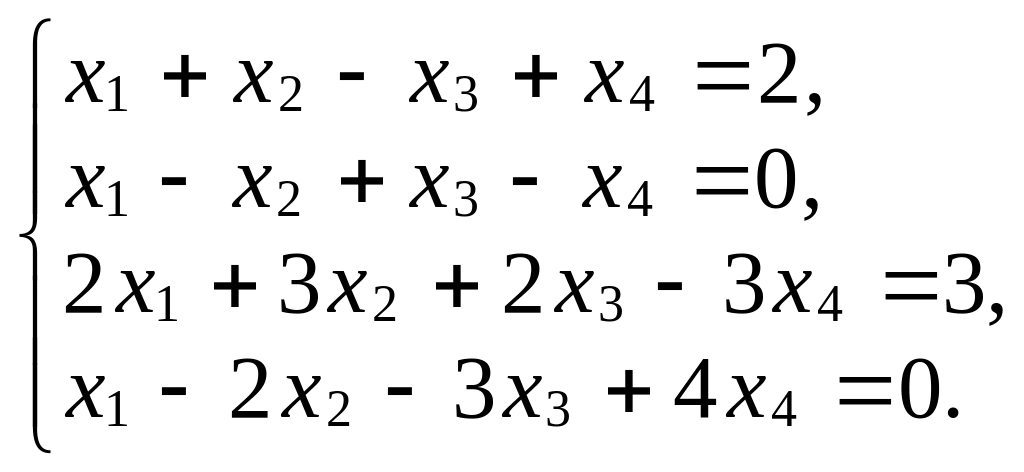
3. Подберите  так, чтобы система уравнений имела решения:

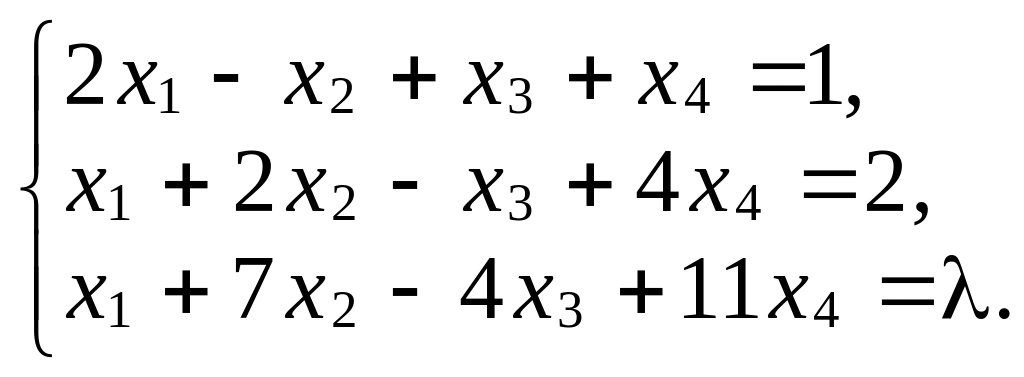
V. Задание на дом

1. Найдите ранг матриц: а) ; б) .

2. Исследуйте, совместны ли системы, и решите их:

а) б)

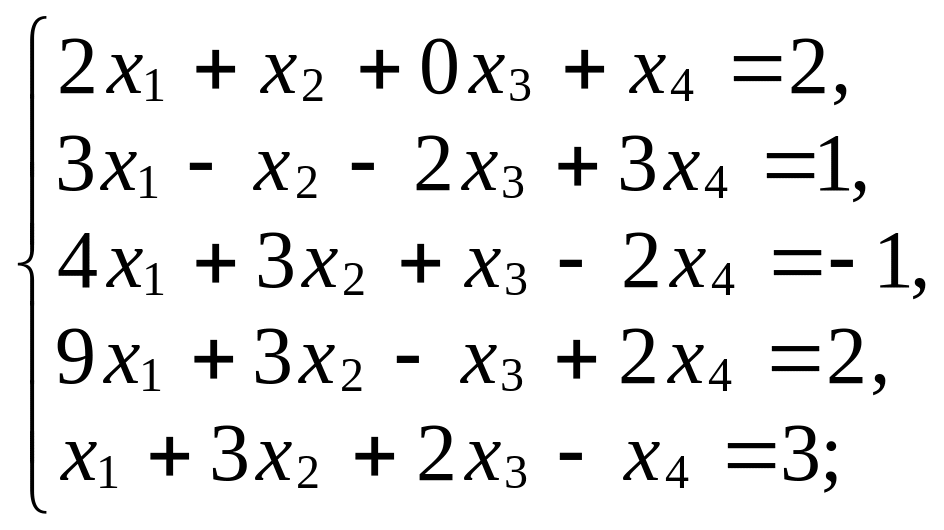
в)

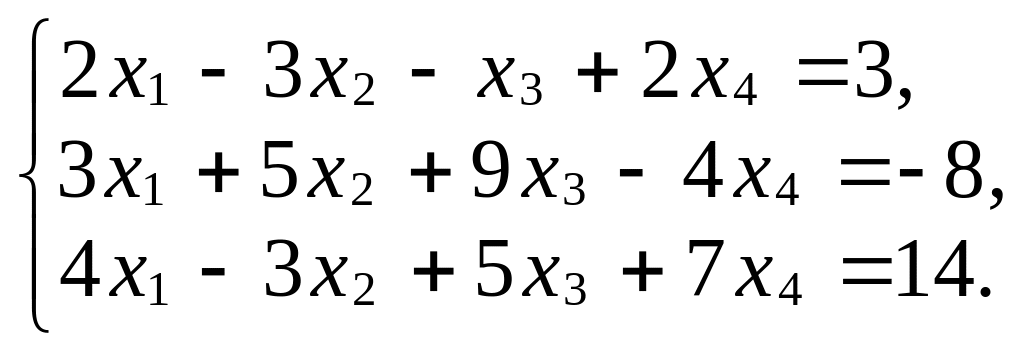
Занятие 4 Тема: «Системы линейных уравнений»

Литература для самостоятельного изучения темы: [1], гл. VII; [2], разд. I, гл. 2; [3], гл. 3; [4], гл. 3; [6], гл. VII; [7], гл. 2; [8], гл. 2; [9], гл. 10; [10], гл. 7.

I. Контрольные вопросы и задания

1. Дайте определение линейного уравнения с n неизвестными.

2. Дайте определение системы линейных уравнений с n неизвестными. Запишите ее в общем виде.

3. Какая система называется однородной?

4. Какая система уравнений называется:

а) совместной; б) несовместной; в) определенной; г) неопределенной?

5. Что значит решить систему?

6. Что называют решением системы?

7. Какие системы называются эквивалентными?

8. Запишите основную и расширенную матрицы системы m линейных уравнений с n неизвестными.

9. Что называют определителем системы?

10. Какие преобразования системы называются элементарными?

11. В чем заключается метод Гаусса решения системы линейных уравнений?

12. Какая система называется невырожденной?

13. Как решить систему матричным способом? К любой ли системе применим данный метод?

14. Как решить систему с помощью формул Крамера? К любой ли системе применим данный метод?

15. Если определитель системы равен нулю, а среди определителей есть отличные от нуля, то какое решение имеет система?

16. Как зависит решение однородной системы линейных уравнений от ее определителя?

II. Типовые задачи с решениями

Задача 1. Решите методом Гаусса системы уравнений:

а) 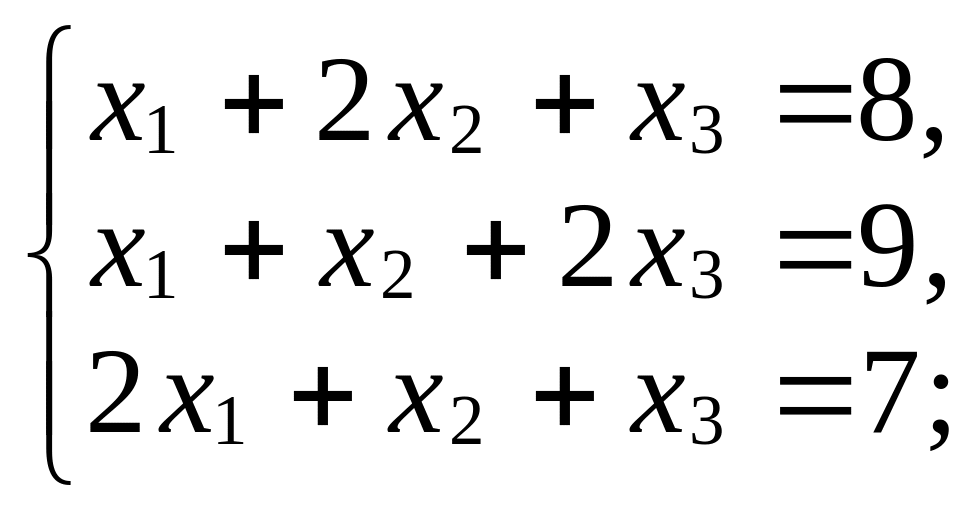б)

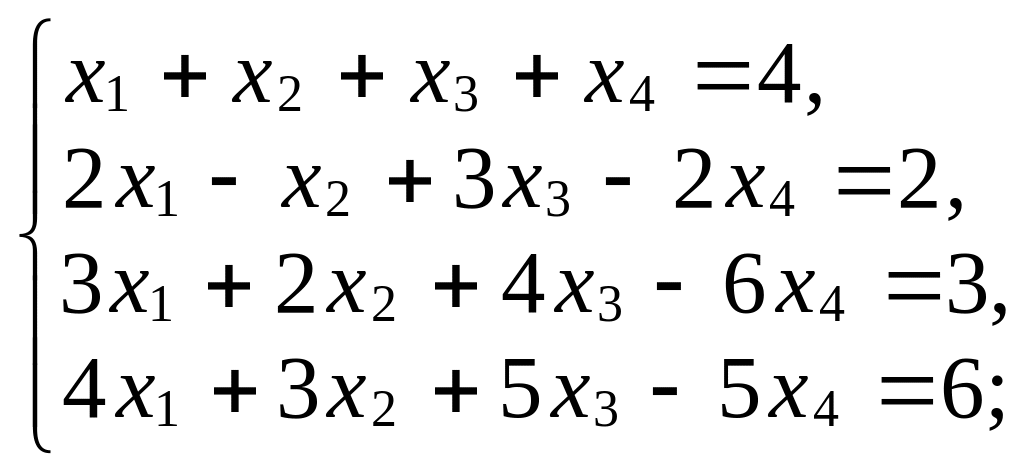
в)

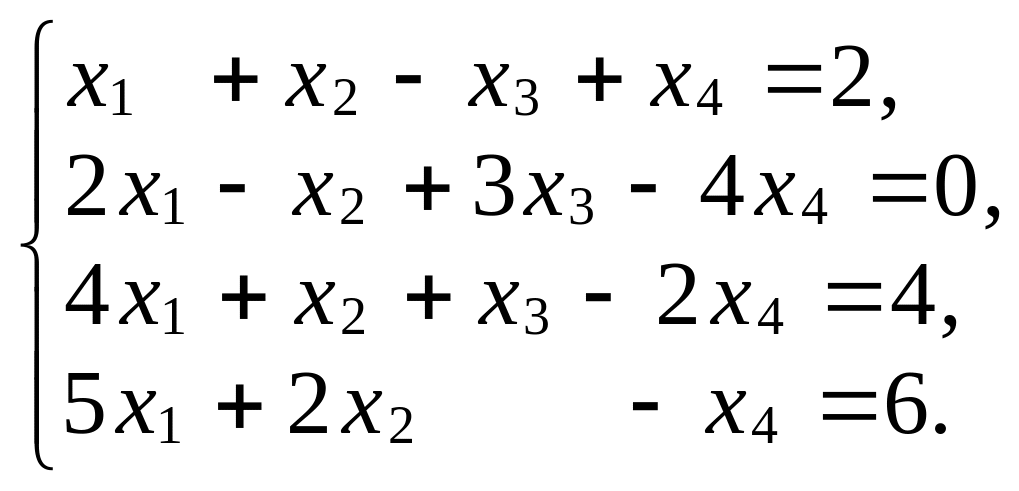
Решение. а) Составим расширенную матрицу В и преобразуем ее к ступенчатому виду: .

Умножим первую строку матрицы В последовательно на – 1 и 2 и сложим соответственно со второй и третьей строками. Получим матрицу, эквивалентную данной: .

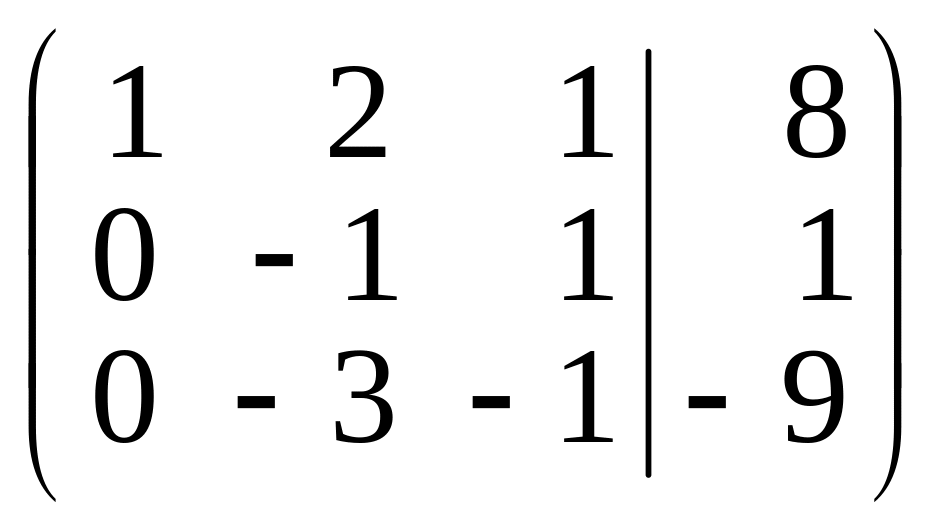Вторую строку умножим на – 3 и сложим с третьей строкой. Получим матрицу, эквивалентную исходной: .

Из коэффициентов последней матрицы составим систему, равносильную исходной:

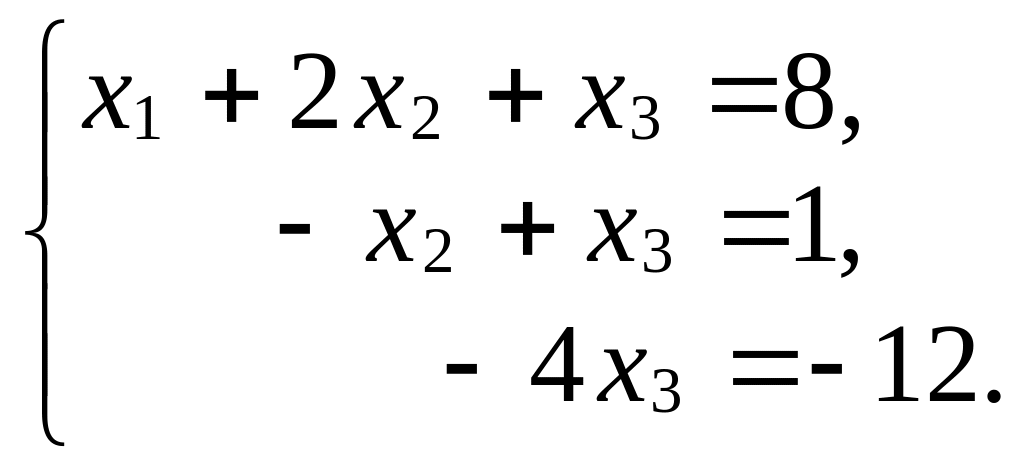
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому.

Ответ:

б) Записывая соответствующую матрицу и совершая преобразования, получаем:

.

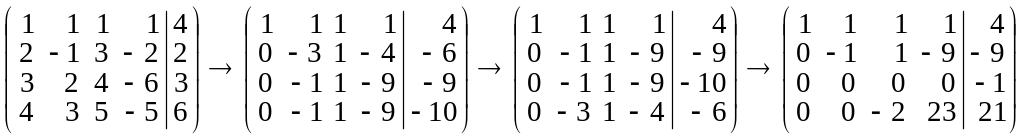Третья матрица получена из предыдущей переменой местами последних трех строк. Последней матрице соответствует система уравнений:

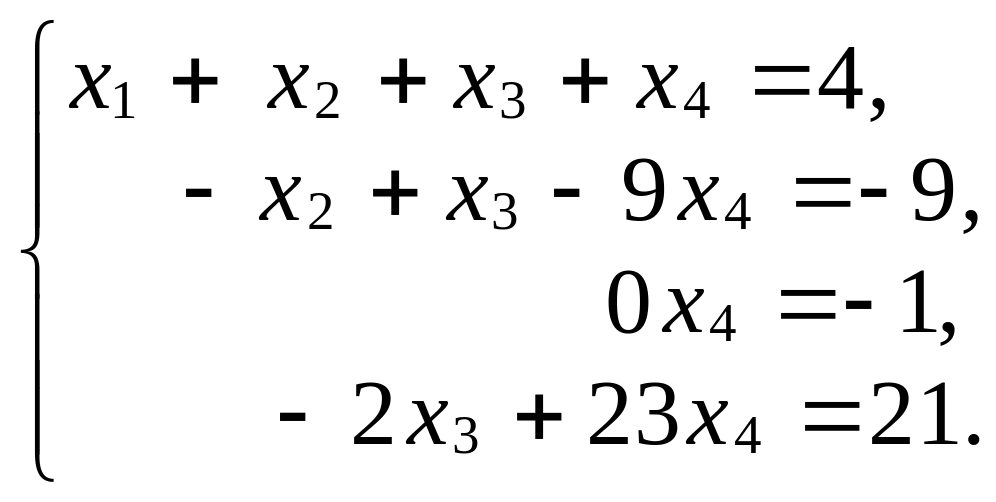
Эта система несовместна, т.к. никакие значения неизвестных не могут удовлетворить ее третьему уравнению.

Ответ: решения нет.

в) Преобразуя матрицу, получаем:

.

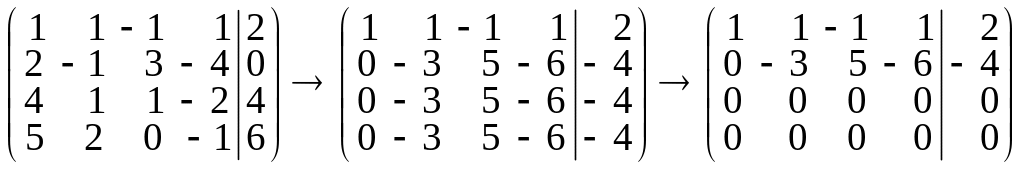Таким образом, данная система сводится к системе двух уравнений относительно четырех неизвестных:

общее решение которой определится формулами: где могут принимать любые действительные числа.

Ответ: .

Задача 2. Решите систему уравнений матричным способом:

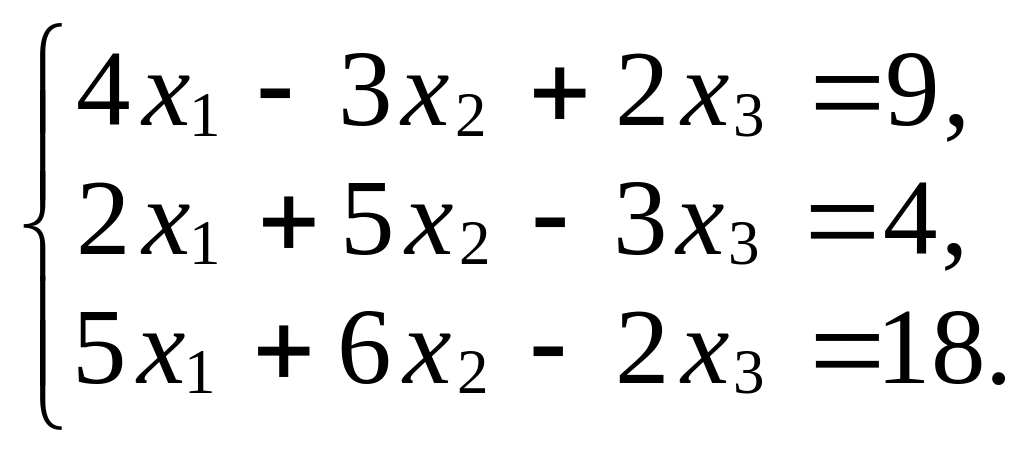
Решение. Данную систему запишем в матричном виде АХ = В, где

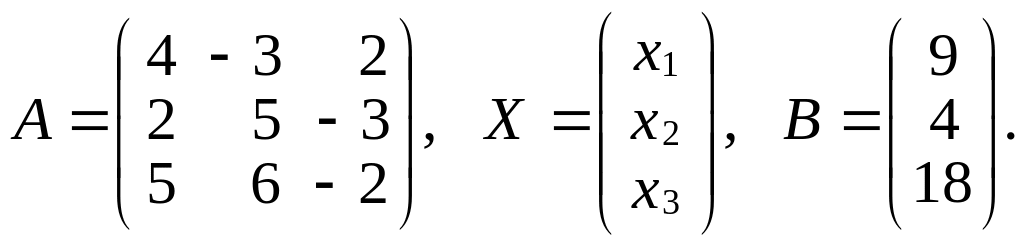
Вычисляем определитель матрицы А и находим матрицу :

По формуле получаем решение системы:

т.е.

Ответ:

Задача 3. Решите систему уравнений по формулам Крамера:

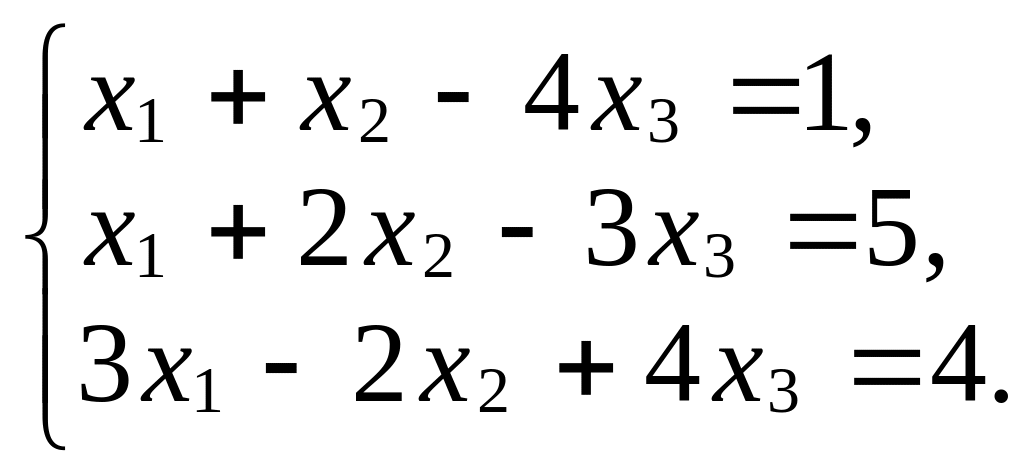
Решение. Вычислим определитель данной системы:

Следовательно, система имеет единственное решение. Заменив в определителе системы последовательно первый, второй и третий столбцы столбцом из свободных членов и вычислив соответствующие определители, будем иметь:

Согласно формулам Крамера получим:

Ответ: