Закон преломления

Отношение синуса угла падения к синусу угла преломления равно показателю преломления второй среды относительно первой:

.

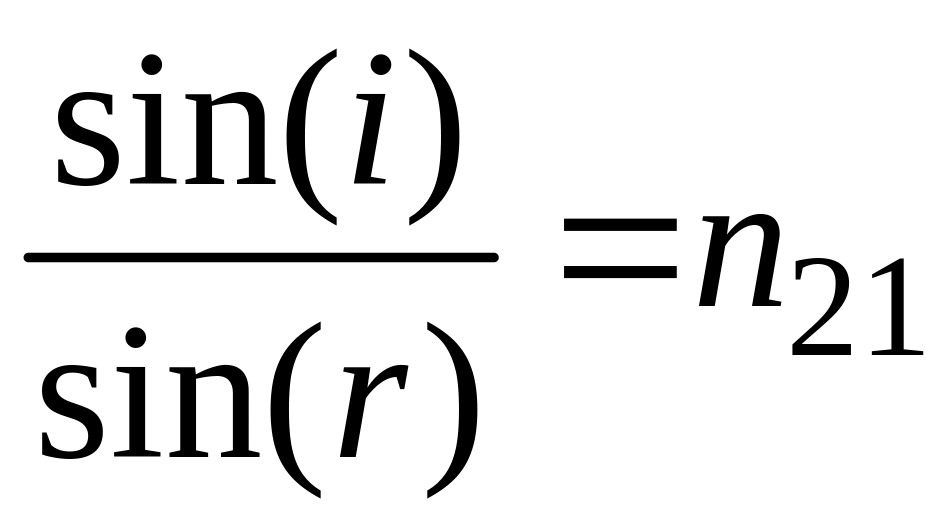Относительный показатель преломления определяется отношением скоростей света в средах, на границе которых происходит преломление, . Кроме того, луч падающий, преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости, называемой плоскостью падения.

Доказательство.

Пусть на границу раздела двух сред падает плоская волна (рис. 11). Фронт этой волны АС перпендикулярен лучам А₁А и В₁В. Фронт преломленной волны можно получить, проведя огибающую вторичных волн во второй среде, центры которых лежат на границе раздела сред. Поверхности MN вначале достигнет луч А₁А. Если скорость света в первой среде равна ₁, то луч В₁В достигнет поверхности MN спустя время t = CB/₁. Поэтому в момент, когда вторичная волна в точке В только начнет возбуждаться, волна в точке А уже будет иметь вид сферы с радиусом AD = ₂t, где ₂ – скорость света во второй среде. Фронт DB преломленной волны получим, если проведем прямую, касательную к этой сфере.

Рассмотрим треугольники САВ и АВD. Это прямоугольные треугольники с общей гипотенузой. Углы падения и преломления входят в эти треугольники как углы с взаимно перпендикулярными сторонами. Следовательно,

ВС = ₁t = ABsin(i),

AD = ₂t = ABsin(r).

Разделив первое уравнение на второе, получим закон преломления

,

где n₂₁ – постоянная величина, не зависящая от угла падения.

Полное внутреннее отражение

Пусть свет распространяется из среды с бóльшим показателем преломления в среду с меньшим показателем преломления. Среда считается оптически более плотной, если ее показатель преломления больше. С увеличением угла падения увеличивается и угол преломления. Когда угол падения достигает некоторого предельного значения, определяемого условием sin(r) = 1, преломленный луч будет распространяться вдоль границы раздела. Закон преломления в этом случае примет вид

sin(i_пред) = .

При еще большем угле i  i_пред остается только один отраженный луч. Это явление носит название полного внутреннего отражения.

Тонкая линза Преломление на сферической поверхности

Р ассмотрим теперь преломление на сферической поверхности радиуса R с центром в точке O. Рассмотрим несколько случаев.

Случай 1 (рис. 12)

Пусть точечный источник света находится на расстоянии d от поверхности стекла (показатель преломления которого n>1). Докажем, что различные лучи, выходящие от источника S под малыми углами к прямой SO, пересекаются в одной точке. Для этого рассмотрим преломление произвольного луча SB, составляющего с осью малый угол . Перпендикуляром к поверхности в точке В служит радиус ОВ, составляющий с осью угол . Обозначим через i угол падения, а через r – угол преломления. Преломленный луч пересекает ось в точке S'. Преломленный луч BS' составляет с осью угол '.

Найдем соотношение между расстояниями SP = d, S'P = f и ОР = R. Учтем, что при малом угле  отрезок PD также мал и им можно пренебречь по сравнению с расстояниями SP, S'P и ОР. Тогда d  SD, f  S'P, R  OD. Из треугольников SBD, S'BD и OBD можно получить следующие равенства

tg   h/d, tg '  h/f и tg   h/R.

Если угол  мал, то малы и углы  и ', и их тангенсы можно заменить значениями самих углов в радианах:

  h/d, '  h/f;   h/R.

Чтобы выяснить, как связаны между собой d, f и R, найдем, как связаны между собой углы , ' и . Угол i является внешним углом треугольника SBO. Поэтому

i =  + .

Угол  – внешний угол треугольника OBS'. Следовательно,

 = r + '  r =  – '.

Т.к. углы малы, то в законе преломления синусы углов можно заменить самими углами: n = sin i /sin r  i/r . Отсюда

i  rn .

Выразим i и r в уравнении через приосевые углы:

 +  = ( – ')n,  + 'n = (n – 1).

Подставляя в выражения и сделав преобразования, получим:

.

В это соотношение не входит h; существенно лишь, чтобы h было мало. Это означает, что все приосевые лучи пересекаются в одной точке S', которая является изображением S. Выражение называют нулевым инвариантом Аббе.