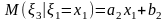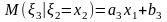2) Построение корреляционного поля и проверка гипотезы о линейной регрессионной зависимости признаков

Графики корреляционного поля для каждой пары признаков, построенные в пакете Excel, представлены на рисунках 2.25-2.27.

Рисунок 2.25 – Корреляционное поле для первого и второго признаков

Рисунок 2.26 – Корреляционное поле для первого и третьего признаков

Рисунок 2.27 – Корреляционное поле для второго и третьего признаков

Во всех трех случаях «облако» точек имеет вытянутую форму. Наиболее ярко линейная зависимость проявляется для первого и второго признаков.

Проверим гипотезу о линейной регрессионной зависимости каждой пары признаков с помощью статистики , распределенной при справедливости выдвинутого предположения по закону Фишера с числом степеней свободы , , где 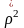– оценка корреляционного отношения признаков, – оценка коэффициента детерминации, n – объем выборки, m – число групп (интервалов) признака, выступающего в качестве результативного.

Как известно, в двумерном случае коэффициент детерминации равен квадрату коэффициента корреляции признаков. Рассчитать выборочные значения коэффициентов корреляции для каждой пары признаков можно с помощью пакета Statistica, выбрав пункты меню «Statistics», «Basic Statistics/Tables» (рисунок 2.28).

Рисунок 2.28 – Пункты меню для расчета выборочных значений коэффициентов корреляции

В появившейся на экране форме (рисунок 2.29) необходимо выбрать пункт «Correlation matrices» и нажать кнопку «ОК».

Рисунок 2.29 – Форма «Basic Statistics/Tables»

Далее на форме, представленной на рисунке 2.30, нажать кнопку «One variable list» для отбора признаков для анализа.

Рисунок 2.30 – Форма расчета коэффициентов корреляции

Для расчета коэффициентов корреляции между каждой парой признаков в окне, представленном на рисунке 2.31, необходимо указать первые три признака и нажать кнопку «ОК».

Рисунок 2.31 – Окно выбора признаков для расчета коэффициентов корреляции

Затем в форме, представленной на рисунке 2.30, нажать кнопку «Summary: Correlations». Результаты расчета корреляционной матрицы представлены на рисунке 2.32.

Рисунок 2.32 – Результаты расчета корреляционной матрицы

Таким образом, выборочные значения коэффициентов детерминации составили:

, , .

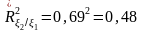Для вычисления выборочных значений корреляционных отношений необходимо на основе интервальных вариационных радов каждого из признаков составить корреляционные таблицы. Интервальные вариационные ряды можно построить на основе рисунков 2.22-2.24. Корреляционная таблица для первого и второго признаков имеет вид:

	[13; 15,25)	[15,25; 17,5)	[17,5; 19,75)	[19,75; 22)	[22; 24,25)	[24,25; 26,5)	[26,5; 28,75)
[4;6)	1	–	–	–	–	–	–	1
[6;8)	1	–	3	1		–	–	5
[8;10)	1	1	6	8	1			17
[10;12)	–	1	8	6	4	2	–	21
[12;14)	–	–	–	2	2	–	–	4
[14;16)	–	–	–	–	–	–	1	1
[16;18]	–	–	–	–	–	–	1	1
	3	2	17	17	7	2	2	50

Выборочное значение корреляционного отношения на рассчитывается по формуле [44]:

,

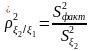где – выборочное значение дисперсии ;

– выборочное значение факторной дисперсии;

– среднее арифметическое значение ;

– среднее значение при условии, что значения принадлежат i-му интервалу;

m – число интервалов в интервальном вариационном ряду .

Значения и можно взять из результатов расчета корреляционной матрицы (рисунок 2.328): , . Условные средние значения составляют: , , , , , , 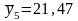. Тогда , .

Аналогичным образом рассчитаны выборочные значения , .

Результаты проверки гипотез о линейной регрессионной зависимости признаков представлены в таблице 2.1.

Таблица 2.1 – Результаты проверки гипотезы о линейной регрессионной зависимости признаков

Нулевая гипотеза
	0,48	0,53	0,91
	0,0004	0,0288	0,25
	0,11	0,1468	0,37

Критическое значение статистики во всех трех случаях составляет . Таким образом, можно сделать вывод в пользу линейной регрессионной связи каждой пары случайных величин вектора .