Глава 1. Кинематика поступательного и вращательного движения материальной точки

Основные формулы

1. Положение материальной точки в пространстве относительно тела отсчета задается радиус  вектором проведенным из начала координат в точку наблюдения:

где , ,  единичные векторы направлений (орты); x,y,z  координаты точки в декартовой системе координат. Модуль радиус  вектора задается как:

2. Скорость движения.

Средняя скорость:

< > ,

где  перемещение материальной точки за промежуток времени .

Мгновенная скорость движущейся точки:

где

 проекции вектора скорости на оси координат.

Модуль мгновенной скорости:

Средняя путевая скорость:

< > ,

где  длина участка траектории, который точка проходит за промежуток времени .

Мгновенная путевая скорость  есть первая производная от пути по времени:

Путь, пройденный точкой за интервал времени от

3. Ускорение точки.

Среднее ускорение:

где – изменение скорости за промежуток времени .

Мгновенное ускорение:

или

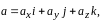
где

 проекции ускорения на оси координат.

Абсолютное значение ускорения:

4. Криволинейное движение.

При криволинейном движении полное ускорение точки разлагают на две составляющие: тангенциальное или касательное ускорение и нормальное или центростремительное ускорение

Тангенциальное ускорение характеризует быстроту изменения скорости по величине, направлено по касательной и выражается формулой:

или

где – единичный вектор касательной, проведенной в точке траектории в направлении скорости точки.

Нормальное ускорение характеризует быстроту изменения скорости по направлению, направлено к центру кривизны траектории и выражается формулой:

или

где R радиус кривизны траектории,  единичный вектор главной нормали.

Модуль вектора полного ускорения:

1.5 Вращение тела вокруг неподвижной оси.

Кинематическим уравнением вращения называется уравнение вида:

где φ  угол между двумя положениями радиус  вектора в момент времени t = 0 и в любой другой момент времени t.

Средняя угловая скорость:

где  изменение угла поворота за время .

Мгновенная угловая скорость (в проекции на ось вращения):

Среднее угловое ускорение:

где  изменение угловой скорости за время

Мгновенное угловое ускорение (в проекции на ось вращения):

Частота вращения (число оборотов в единицу времени):

или

где N  число оборотов, совершаемых за время t, T  период вращения (время одного оборота ).

5. Связь между линейными и угловыми величинами, характеризующими вращение материальной точки:

длина дуги, пройденная точкой,

где  угол поворота тела, R  радиус вращения точки;

линейная скорость точки:

тангенциальное ускорение точки:

нормальное ускорение точки:

Таблица 1.1 Аналогия равнопеременного поступательного и вращательного движения

Поступательное движение	Вращательное движение
При ускоренном движении а>0, При замедленном движении а<0.	При ускоренном движении >0, При замедленном движении <0.