§3. Методы первого и второго порядка

Методы первого и второго порядков рассмотрим на примере методов градиентного спуска с постоянным шагом и метода Ньютона.

3.1. Метод градиентного спуска с постоянным шагом

Напомним, что в большинстве случаев численные методы минимизации основываются на построении итерационной последовательности {X_k}, обладающей свойством f(X_k+1)<f(X_k), (k=0, 1, …), по формулам X_k+1=X_k+h_kD_k, D_k  направление спуска, h_k  величина шага. Если D_k=f(X_k), то метод называется градиентным. Если величину шага h_k оставлять постоянной (до тех пор, пока функция убывает в точках последовательности), то метод называется методом градиентного спуска с постоянным шагом. Убывание контролируется путём проверки выполнения условия f(X_k+1)f(X_k)<0. Построение последовательности {X_k} заканчивается в точке X_k, для которой |f(X_k)|<₁, или выполняется система

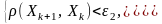
где ₁, ₂  заданные положительные числа, или kk₀, где k₀  предельное число итераций. Дополнительно необходимо провести исследование вопроса, является ли найденная точка действительным приближением искомой функции.

Более подробно:

1. Задать X₀, ₁>0, ₂>0, k₀. Найти градиент функции f(X)= , …, (Напоминаем, что в отношение вектора возможно одновременное применение в качестве обозначений как строки, так и столбца. При чтении произведений типа AX или XA, где X  вектор, а A  (mn)-матрица, разночтений быть не должно: в первом случае  это столбец с n элементами, во втором  строка с m элементами).

2. Положить k=0.

3. Вычислить f(X_k).

4. Проверить критерий окончания |f(X_k)|₁:

а) если критерий выполнен, то расчёт закончен: X^*=X_k;

б) если критерий не выполнен, то перейти к шагу 5.

5. Проверить выполнение неравенства kk₀:

а) если неравенство выполнено, то расчёт окончен: X^*=X_k;

б) если нет, то перейти к шагу 6.

6. Задать величину шага h_k.

7. Вычислить X_k+1=X_kh_kf(X_k).

8. Проверить выполнение условия f(X_k+1)f(X_k)<0:

а) если условие выполнено, то перейти к шагу 9;

б) если условие не выполнено, то положить h_k=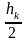 и перейти к шагу 7.

9. Проверить условия (X_k+1, X_k)<₂ и |f(X_k+1)f(X_k)|<₂:

а) если оба условия выполнены при текущем значении k и k1, то расчёт окончен: X^*=X_k;

б) если хотя бы одно условие не выполнено, то положить k=k+1 и перейти к шагу 3.

Вопрос о сходимости последовательности {X_k} к решению X^* решается в общем в случае с помощью так называемого условия Липшица. Мы ограничимся тем фактом, что если f(X)  сильно выпуклая функция, то при любом выборе X₀ последовательность {X_k}, полученная методом градиентного спуска, сходится к точке X^*. Поэтому прежде, чем начинать строить последовательность {X_k}, необходимо проверить условие сильной выпуклости функции.

После окончания процедуры нахождения X*X_k, необходимо проверить, что найденная точка, действительно, является приближением решения задачи.

Если f(X)  дважды непрерывно дифференцируемая (а мы ограничимся именно этим классом задач), то при H(X_k)>0 точка X_k является приближением искомой точки.

Пример I. Найти локальный минимум функции

f(x₁, x₂)=3 +2x₁x₂+2 .

Решение. Прежде всего убедимся, что функция выпукла. Так как H(X)=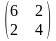 , то H(X)>0 и функция сильно выпукла, и сходимость итерационного процесса гарантирована.

I. Найдём X_k.

1. Зададим X₀=(1, 1), ₁=0,1, ₂=0,1, k₀=10 и найдём градиент f(X)=(6x₁+2x₂, 2x₁+4x₂).

2. Положим k=0.

3.0. Вычислим f(X₀)=(8; 6).

4.0. Вычислим |f(X₀)| и проверим критерий окончания: |f(X₀)|=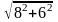 =10>0,1. Переходим к шагу 5.

5.0. Проверим условие k>k₀: k=0<10=k₀. Переходим к шагу 6.

6.0. Зададим h₀=0,2.

7.0. Вычислим X₁=X₀0,2f(X₀)=(1; 1)0,2(8; 6)=(0,6; 0,2).

8.0. Проверим выполнение условия f(X₁)f(X₀)<0. Так как f(X₁)=1,4, f(X₀)=7, то условие выполняется. Переходим к шагу 9.

9.0. Проверим условия (X₁, X₀)<0,1 и |f(X₁)f(X₀)|<0,1. Второе условие не выполняется: |f(X₁)f(X₀)|=5,6>0,1. Полагаем k=1 и переходим к шагу 3.

3.1. Вычислим f(X₁)=(4; 2).

4.1. Вычислим |f(X₁)| и проверим критерий окончания: |f(X₁)|=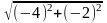 = >0,1. Переходим к шагу 5.

5.1. Проверим условие k>k₀: k=1<10=k₀. Переходим к шагу 6.

6.1. Зададим h₁=0,2.

7.1. Вычислим X₂=X₁0,2f(X₁)=(0,6; 0,2)0,2(4; 2)=(0,2; 0,2).

8.1. Проверим выполнение условия f(X₂)f(X₁)<0. Так как f(X₂)=0,28, f(X₁)=1,4, то условие выполняется: f(X₂)f(X₁)=0,281,4=1,12. Переходим к шагу 9.

9.1. Проверим условия (X₂, X₁)<0,1 и |f(X₂)f(X₁)|<0,1. Второе условие не выполняется: |f(X₂)f(X₁)|=1,12>0,1. Полагаем k=2 и переходим к шагу 3.

3.2. Вычислим f(X₂)=(1,6; 1,2).

4.2. Вычислим |f(X₁)| и проверим критерий окончания: |f(X₁)|= =2>0,1. Переходим к шагу 5.

5.2. Проверим условие k>k₀: k=2<10=k₀. Переходим к шагу 6.

6.2. Зададим h₂=0,2.

7.2. Вычислим X₃=X₂0,2f(X₂)=(0,2; 0,2)0,2(1,6; 1,2)=(0,12; 0,04).

8.2. Проверим выполнение условия f(X₃)f(X₂)<0. Так как f(X₃)=0,056, f(X₂)=0,28, то условие выполняется: f(X₃)f(X₂)=0,224. Переходим к шагу 9.

9.2. Проверим условия (X₃, X₂)<0,1 и |f(X₃)f(X₂)|<0,1. Второе условие не выполняется: |f(X₃)f(X₂)|=0,224>0,1. Полагаем k=3 и переходим к шагу 3.

3.3. Вычислим f(X₃)=(0,8; 0,4).

4.3. Вычислим |f(X₃)| и проверим критерий окончания: |f(X₃)|=0,8944>0,1. Переходим к шагу 5.

5.3. Проверим условие k>k₀: k=3<10=k₀. Переходим к шагу 6.

6.3. Зададим h₃=0,2.

7.3. Вычислим X₄=X₃0,2f(X₃)=(0,12; 0,02)0,2(0,8; 0,4)=(0,04; 0,04).

8.3. Проверим выполнение условия f(X₄)f(X₃)<0. Так как f(X₄)=0,0112, f(X₃)=0,056, то условие выполняется: f(X₄)f(X₃)=0,0448. Переходим к шагу 9.

9.3. Проверим условия (X₄, X₃)<0,1 и |f(X₄)f(X₃)|<0,1. Второе условие выполняется: |f(X₄)f(X₃)|=0,0448<0,1. Для первого имеем

(X₄, X₃)=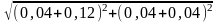 = 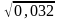0,1789>0,1,

и условие не выполняется. Полагаем k=4 и переходим к шагу 3.

3.4. Вычислим f(X₄)=(0,32; 0,24).

4.4. Вычислим |f(X₄)| и проверим критерий окончания: |f(X₄)|=0,4>0,1. Переходим к шагу 5.

5.4. Проверим условие k>k₀: k=4<10=k₀. Переходим к шагу 6.

6.4. Зададим h₄=0,2.

7.4. Вычислим X₅=X₄0,2f(X₄)=(0,04; 0,04)0,2(0,32; 0,24)=(0,024; 0,008).

8.4. Проверим выполнение условия f(X₅)f(X₄)<0. Так как f(X₅)=0,0022, f(X₄)=0,0112, то условие выполняется: f(X₅)f(X₄)=0,009. Переходим к шагу 9.

9.4. Проверим условия (X₅, X₄)<0,1 и |f(X₅)f(X₄)|<0,1. Второе условие выполняется: |f(X₅)f(X₄)|=0,009<0,1. Для первого имеем

(X₅, X₄)=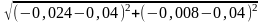 = 0,08<0,1,

и условия выполняются. Условия должны выполняться для текущего k и k1. Поэтому полагаем k=5 и переходим к шагу 3.

3.5. Вычислим f(X₅)=(0,16; 0,08).

4.5. Вычислим |f(X₅)| и проверим критерий окончания: |f(X₅)|=0,1799>0,1. Переходим к шагу 5.

5.5. Проверим условие k>k₀: k=5<10=k₀. Переходим к шагу 6.

6.5. Зададим h₅=0,2.

7.5. Вычислим

X₆=X₅0,2f(X₄)=(0,024; 0,008)0,2(0,16; 0,08)=(0,008; 0,008).

8.5. Проверим выполнение условия f(X₆)f(X₅)<0. Так как f(X₆)=0,0005, f(X₅)=0,0022, то условие выполняется: f(X₆)f(X₅)=0,0017. Переходим к шагу 9.

9.5. Проверим условия (X₆, X₅)<0,1 и |f(X₆)f(X₅)|<0,1. Второе условие выполняется: |f(X₆)f(X₅)|=0,0017<0,1. Для первого имеем

(X₆, X₅)= 0,0358<0,1.

Так как оба условия выполнены при текущем значении k=5 k1=4, то расчёт окончен: X*=X₅=(0,024; 0,008).

II. Анализ точки X₅.

Функция f(x₁, x₂)=3 +2x₁x₂+2 является дважды дифференцируемой. Так как матрица Гессе  постоянна и является положительно определённой, то точка X₅ является точкой локального минимума, а значение f(X₅)=0,0022  приближённое значение локального минимума.

Ответ: точкой локального минимума является точка X^*=(0,024; 0,008), f(X^*)=0,0022  локальный минимум.