Разработка и исследование рекуррентных моделей вычислений

1 Цель занятия

Получить первичные навыки составления алгоритмов компьютерных моде­лей на основе рекуррентных моделей вычислений.

2 Оборудование рабочего места и программное обеспечение

Персональный компьютер.

Программное обеспечение: Microsoft Office Visio 2007

3 Краткие теоретические сведения

Рекуррентные и рекурсивные вычисления являются одними из широко применяемых в алгоритмах, так как они позволяют программировать процессы, развивающиеся во времени (динамические процессы).

Рекуррентной называе6тся последовательность, в которой каждый последующий элемент определяется через один или несколько предыдущих элементов.

Формула, определяющая произвольный элемент последовательности через предыдущие элементы, называется рекуррентной формулой. Она имеет вид:

A(i) = F(A(i-1), A(i-2),…, A(i-k))

Здесь k называется глубиной рекурсии.

Суть метода рекуррентных соотношений заключается в выполнении следующих шагов:

• на основе содержательной постановки задачи получить математическое описание рекуррентного соотношения;

• на основе выбранных структур данных и модели вычислений разработать алгоритм и программу на выбранном языке программирования.

Используемая литература.

1. Петушкова Е.П. Учебное пособие по дисциплине «Основы алгоритмизации и программирования», тема 1.3.

2. Семакин И.Г., Шестаков А.П. Основы программирования, стр. 281-284.

3. Шишковский С.А. Компьютерное моделирование. Методические указания для студентов заочной формы обучения. Тема 2.1.

4 Порядок выполнения работы

1. Переписать задание к работе в тетрадь.

2. Выполнить задание

3. Ответить на контрольные вопросы.

5 Содержание отчета

1. Наименование практической работы.

2. Цель работы.

3. Конкретное задание и его выполнение.

4. Ответы на контрольные вопросы.

6 Контрольные вопросы

1. Каковы принципы организации рекуррентных моделей вычислений?

2. Каковы правила построения рекуррентных соотношений?

7 Варианты заданий к практическому занятию №7

Вариант № 1

1. В ычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить для вычисления суммы степенного ряда по схеме Горнера.

В ариант № 2

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 3

1. Вычислить сумму ряда Y= 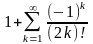. Вычисления продолжать, пока очередной член ряда не станет меньше 0,0001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 4

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока разность между соседними членами не станет меньше 0,001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 5

1. Вычислить сумму ряда Y= Вычисления продолжать, пока очередной член ряда не станет меньше 0,0001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 6

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,01.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 7

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,0001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 8

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,001.

2. И зменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

В ариант № 9

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,001.

2. Изменить вид представления степенного ряда в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

Вариант № 10

1. Вычислить сумму ряда Y= . Вычисления продолжать, пока очередной член ряда не станет меньше 0,0001.

2. Изменить вид представления степенного ряд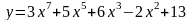а в соответствии со схемой Горнера. Составить программу для вычисления суммы степенного ряда по схеме Горнера.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8.

Решение задач с применением множеств