
- •-Державний вищий навчальний заклад «Чернігівський технікум транспорту та комп’ютерних технологій»
- •1 Пояснювальна записка
- •Витяг із робочої програми
- •Теми практичних занять
- •Перелік посилань
- •3 Зміст практичних занять практичне заняття № 1 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 2 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 3 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 4 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 5 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 6 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 7 (2 год.)
- •Зміст практичного заняття
- •Н а колі всі точки мають однаковий потенціал, отже
- •Практичне заняття № 8 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 9 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 10 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 11 (2 год.)
- •Зміст практичного заняття
- •Зміст практичного заняття
- •Практичне заняття № 14 (2 год.)
- •Зміст практичного заняття
- •Зміст практичного заняття
- •Практичне заняття № 16 (2 год.)
- •Зміст практичного заняття
- •Практичне заняття № 17 (2 год.)
- •Зміст практичного заняття
- •Остаточна оцінка визначається за таблицею
- •Критерії характеристики рівнів
- •Практичне заняття № 18 (2 год.)
- •Зміст практичного заняття
Зміст практичного заняття
Розв’язування задач на коливання маятників
Задача
1 До нижнього кінця пружини, підвішеної
вертикально, приєднана друга пружина,
до кінця якої прикріплений вантаж.
Коефіцієнти жорсткості пружини становлять
відповідно k1=300
Н/м
і k1=750
Н/м.
Нехтуючи силою тяжіння пружин порівняно
з силою тяжіння вантажу, знайти відношення
потенційних енергій цих пружин
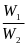 .
.
Дано:
k1=300 Н/м
k1=750 Н/м
____________
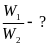
Розв’язок
Під дією сили вантажу масою m обидві пружини розтягуються відповідно на l1 i l2. Виконана вантажем робота з розтягування пружин йде на збільшення потенціальної енергії пружин. Робота, виконана вантажем з розтягування першої пружини:
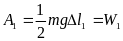 ,
,
а робота з розтягування другої пружини:
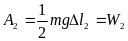
Оскільки
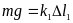 ,
,
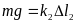
то
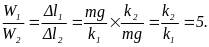
Відповідь.
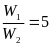 .
.
Задача 2 Частинка масою m=0,01 кг здійснює гармонічні коливання з періодом Т=2 с. Повна енергія частинки, що коливається Е=0,1 мДж. Визначити амплітуду коливань А і найбільшу силу F , що діє на частинку.
Дано:
m=0,01 кг
Т=2 с
Е=0,1 мДж
_______________
А-?, F-?
Розв’язок
Для визначення амплітуди коливань використаємо вираз для повної енергії частинки:
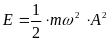 ,
,
де
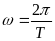 .
.
Звідси амплітуда:
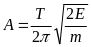 =0,045
м.
=0,045
м.
Оскільки частинка здійснює гармонічні коливання, то сила, яка діє на неї, є квазіупружною і може бути виражена співвідношенням:
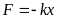 ,
,
де k-коефіцієнт квазіупружної сили, х – зміщення точки, що коливається.
Максимальна сила буде при максимальному зміщенні хmax=A:
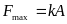 .
.
Коефіцієнт квазіупружної сили:
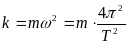 .
.
Тоді:
 =4,44
Н.
=4,44
Н.
Відповідь. А=0,045 м, F=4,44 Н.
Задача 3 Матеріальна точка масою m = 50 г виконує гармонічні коливання з частотою = 2 Гц. Амплітуда коливань А = 10 см. Визначити швидкість точки на момент часу, коли х = 0,5 с, максимальну силу, яка діє на точку та повну енергію її коливань.
 Дано: Рівняння
гармонічного коливання має вигляд:
Дано: Рівняння
гармонічного коливання має вигляд:
m = 50 г = 510-2 кг х = ACos( t+0). Звідки: Cos( t+0) = х/А.
= 2 Гц Формулу швидкості отримаємо
А = 10 см = 0,1 м х = dx/dt = –A Sin( t+0). Звідси:
x
=
6 см = 0,06 м
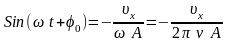 ,
оскільки
= 2.
,
оскільки
= 2.
V, Fmax, W –? Урахувавши, що Cos2( t+0) + Sin2( t+0) = 1,
отримуємо:
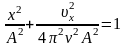 .Звідси:
.Звідси:
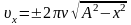 ,
,
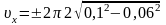
1,0 (м/с).
1,0 (м/с).
Максимальну силу, яка діє на точку, знайдемо з 2-го закону Ньютона: Fmax = mamax, де amax – максимальне (амплітудне) значення прискорення, яке отримаємо з другої похідної:
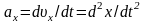 =
–A
2
Cos(
t+0),
або
aх
=
–A 4
2
2Cos(
t+0).
=
–A
2
Cos(
t+0),
або
aх
=
–A 4
2
2Cos(
t+0).
Звідси:
аmax
=
4
2
2A,
 ,
Fmax
=
4
222
0,1510–2
0,8 (Н).
,
Fmax
=
4
222
0,1510–2
0,8 (Н).
Повна
енергія точки дорівнює максимальній
потенціальній або кінетичній енергії.
Звідси:
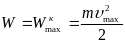 ,
де max
=
A
= 2А,
тобто:
,
де max
=
A
= 2А,
тобто:
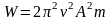 .
.
W = 2 2220,12510–2 0,04 (Дж).
Відповідь: 1 м/с, 0,8 Н, 0,04 Дж.
Задача 4 На кінцях невагомого стрижня завдовжки l = 1,0 м закріплено два тягарці, масою m i 2m. Визначити зведену довжину L і період коливань T даного фізичного маятника відносно горизонтальної осі, що проходить через середину стрижня.

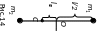 Дано:
Період коливань фізичного маятника
визначається
Дано:
Період коливань фізичного маятника
визначається
l
= 1,0 м з
формули:
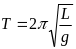 ,
де L
– зведена довжина
,
де L
– зведена довжина
m1
=
m фізичного
маятника:
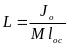 .
.
m2 = 2m інерції маятника відносно осі коливань – т. О,
g = 9,8 м/с2 M = m1+m2 = 3m – його маса, loc – відстань від
L, T –? центра мас т. С маятника до осі коливань т. О.
Момент
інерції маятника: Jo
=
J1
+
J2
=
m1(l/2)2
+
m2(l/2)2
=
m(l/2)2
+
2m(l/2)2
=
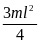
. Відстань loc від осі коливань т.О до центра мас т. С дорівнює:
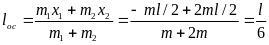 ,
де х1
= -l/2
–
відстань від першого тягарця до осі
коливань
т. О,
х2
= l/2
–
відстань від другого тягарця до осі
коливань.
,
де х1
= -l/2
–
відстань від першого тягарця до осі
коливань
т. О,
х2
= l/2
–
відстань від другого тягарця до осі
коливань.
Підставляючи до відповідної формули, отримуємо:
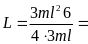
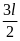 ,
,
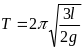 .
.
Обчислюємо:
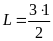 = 1,5(м),
= 1,5(м),
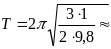 2,46(с).
2,46(с).
Відповідь: 2,46 с.
Розв’язування задач на коливання точки
Задача 1 Точка бере участь у двох коливаннях поперечного напрямку х = AСost і y = ВSint, де А = 3 см, В = 2 см. Знайти рівняння траєкторії y(x) результуючого коливання і побудувати його, указавши напрямок руху точки вздовж траєкторії.
 Дано:
Дано:
 х
= A Cos t
х
= A Cos t
y = B Sin t
А = 3 см = 310-2 м
B = 2 см = 210-2 м
y(х) – ?
Запишемо рівняння коливань у вигляді
:
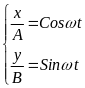 і далі:
і далі:
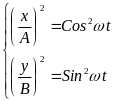
Звідки,
додавши ці рівняння і врахувавши, що
 ,
маємо:
,
маємо:
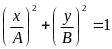 або
або
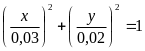 .
.
Це
рівняння еліпса, з напівосями А
і В
. Щоб визначити напрямок руху точки по
траєкторії, визначимо спочатку положення
точки у момент часу t = 0:
x0 = AСos0 = A,
y0 = BSin0 = 0.
Якщо
 ,
тоді
x>0,
y>0,
тобто
точка починає рухатися проти годинникової
стрілки, як і показано на рисунку.
,
тоді
x>0,
y>0,
тобто
точка починає рухатися проти годинникової
стрілки, як і показано на рисунку.
Задача
2 Частинка масою m
=
0,01 кг здійснює гармонічні коливання з
періодом T
=
2 с. Повна енергія частинки, що коливається,
становить E
= 0,1 мДж. Визначити амплітуду А
коливань і найбільше значення сили
![]() що діє на частинку.
що діє на частинку.
Розв’язання. Для визначення амплітуди коливань скористаємося виразом повної енергії частинки:
![]()
де
![]() Звідси амплітуда
Звідси амплітуда
![]() .
.
Оскільки
частинка здійснює гармонічні коливання,
то сила, що діє на неї, є квазіпружною
і, отже, може бути виражена співвідношенням
F=-kx,
де k
- коефіцієнт квазіпружної сили; x
- зміщення точки, що коливається.
Максимальною сила буде при максимальному
зміщенні
![]() ,
що дорівнює амплітуді:
,
що дорівнює амплітуді:
![]() .
.
Коефіцієнт k виразимо через період коливань:
![]()
Підставивши вирази і провівши спрощення, отримаємо
![]()
Проведемо обчислення:
![]()
![]()
Відповідь:
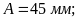
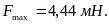
Задача
3 Складаються два коливання однакового
напрямку, що описуються рівняннями
![]() де
де
![]() = 3 cм
= 3 cм
![]() = 2 см
= 2 см
![]() = 1/6 с
= 1/6 с
![]()
![]() =
1/3 с, Т=2
с. Побудувати векторну діаграму складання
цих коливань і написати рівняння
результуючого коливання.
=
1/3 с, Т=2
с. Побудувати векторну діаграму складання
цих коливань і написати рівняння
результуючого коливання.
Розв’язання.
Для побудови векторної діаграми складання
двох коливань одного напрямку треба
зафіксувати який-небудь момент часу.
Як правило, векторну діаграму будують
для моменту часу t
= 0. Перетворивши обидва рівняння до
канонічної форми
![]() ,
отримаємо
,
отримаємо
![]()
Звідси
бачимо, що обидва гармонічні коливання,
які складаються, мають однакову циклічну
частоту
![]() .
.
Початкові фази першого і другого коливань відповідно дорівнюють
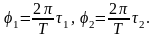
Проведемо обчислення:
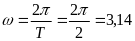 с-1,
с-1,
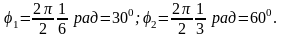
Зобразимо
вектори
![]() і
і
![]() .
Для цього відкладемо відрізки довжиною
= 3 см і
= 2 см під кутами
.
Для цього відкладемо відрізки довжиною
= 3 см і
= 2 см під кутами
![]() = 300
і
= 300
і
![]() =
600
до осі Ох.
Результуюче коливання відбуватиметься
з тією ж частотою
=
600
до осі Ох.
Результуюче коливання відбуватиметься
з тією ж частотою
![]() і амплітудою А,
що дорівнює геометричній сумі амплітуд
і
:
і амплітудою А,
що дорівнює геометричній сумі амплітуд
і
:
![]() .
Згідно з теоремою косинусів
.
Згідно з теоремою косинусів
![]()
Початкову фазу результуючого коливання можна також визначити безпосередньо з векторної діаграми (рис.49):


Рисунок Додавання коливань, що відбуваються у одному напрямку
![]()
Проведемо обчислення:
![]() =4,84
см.
=4,84
см.
![]()
або
![]() =0,735
рад.
=0,735
рад.
Оскільки результуюче коливання є гармонічним, має ту саму частоту, що і складові коливання, то його можна записати у вигляді
,
де
А
= 4,84 см
=
3,144
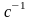 ,
= 0,735 рад.
,
= 0,735 рад.
Відповідь: , де А = 4,84 см = 3,144 , = 0,735 рад.
Задача
4 Матеріальна точка здійснює гармонійні
коливання. В деякий момент часу t
зміщення
точки
x
=
5 см, її швидкість v=
20 см/с і прискорення
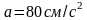 .
Знайти циклічну частоту
,
період коливань Т, фазу коливань та
амплітуду.
.
Знайти циклічну частоту
,
період коливань Т, фазу коливань та
амплітуду.
Розв’язування
Запишімо рівняння гармонійного коливання, швидкості і прискорення:
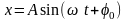 ; (1)
; (1)
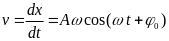 ; (2)
; (2)
:
 . (3)
. (3)
Поділивши
(3) на (1), бачимо, що модуль
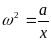 ,
звідси знаходимо циклічну частоту:
,
звідси знаходимо циклічну частоту:
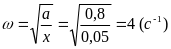
Визначмо період коливань:
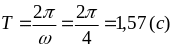 .
.
Щоб визначити фазу коливань поділимо рівняння (1) на (2):
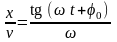 ,
звідки
,
звідки
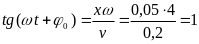 ,
або
,
або
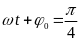 .
.
За рівнянням (1) обчислимо амплітуду:
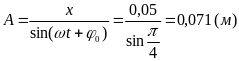 .
.
Відповідь: 0,071 м.
ЗАКРІПЛЕННЯ ВИВЧЕНОГО І ОЦІНЮВАННЯ РІВНЯ ЗНАНЬ:
Розв’язування задач:
Варіант 1
За 5 с маятник зробив 10 коливань. Чому дорівнює період коливань?
А. 5 с Б. 2 с В. 0,5 с Г. 50 с
Як зміниться період коливань вантажу на пружині, якщо масу вантажу збільшити в 4 рази?
А. Збільшиться в 4 рази Б. Збільшиться в 2 рази
В. Зменшиться в 2 рази Г. Зменшиться в 4 рази
Як зміниться період коливань вантажу на пружині, якщо твердість пружини збільшити в 4 рази?
А. Збільшиться в 4 рази Б. Збільшиться в 2 рази
В. Зменшиться в 2 рази Г. Зменшиться в 4 рази
Координата тіла, яке коливається змінюється за законом х = cos ( t/2 ). Чому дорівнює частота коливань? Усі величини подані в одиницях СІ.
А. ¼ Гц Б. ½ Гц В. 2 Гц Г. 4 Гц
Яким виразом визначається період коливань математичного маятника?
А.
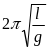 Б.
Б.
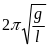 В.
В.
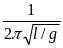 Г.
Г.
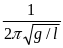
Який приблизно період коливань математичного маятника довжиною 40 м? Прийняти прискорення вільного падіння g = 10 м/с2.
А. 12 з Б. 1/12 с. В. 2 с. Г. 1/2 с.
Як зміниться період коливань математичного маятника, якщо його довжина зменшилася в 9 разів?
А. Збільшиться в 3 рази Б. Збільшиться в 9 рази
В. Зменшиться в 3 рази Г. Зменшиться в 9 рази
Яке з перерахованих коливань є вимушеним? а) Коливання вантажу на нитці, один раз відведеного від положення рівноваги і відпущеного; б) Коливання гойдалки, розгойдуваної людиною, що стоїть на землі.
А. Тільки а) Б. а) і б) У. Тільки б) Г. Ні а), ні б)
Вантаж підвішений на нитці і відхилений від положення рівноваги так, що його висота над землею збільшилася на 45 см. Приблизно з якою швидкістю тіло буде проходити положення рівноваги при вільних коливаннях?
А. 2 м/с Б. 3 м/с В. 9 м/с Г. 30 м/с.
При вільних коливаннях вантажу на пружині максимальне значення його потенціальної енергії 5 Дж, максимальне значення кінетичної енергії 5 Дж. У яких межах змінюється повна механічна енергія вантажу і пружини?
А. Змінюється від 0 до 5 Дж Б. Змінюється від 0 до 10 Дж
В. Не змінюється і дорівнює 5 Дж Г. Не змінюється і дорівнює 10 Дж
Варіант 2
За 6 с маятник зробив 12 коливань. Чому дорівнює частота коливань?
А. 0,5 Гц Б. 2 Гц В. 72 Гц Г. 6 Гц
Як зміниться період коливань вантажу на пружині, якщо масу вантажу зменшити в 4 рази?
А. Збільшиться в 4 рази Б. Збільшиться в 2 рази
В. Зменшиться в 2 рази Г. Зменшиться в 4 рази
Як зміниться період коливань вантажу на пружині, якщо твердість пружини зменшити в 16 разів?
А. Збільшиться в 4 рази Б. Збільшиться в 16 разів
В. Зменшиться в 16 разів Г. Зменшиться в 4 рази
Координата тіла, яке коливається змінюється за законом х = sin ( t ). Чому дорівнює період коливань? Усі величини виражені в одиницях СІ.
А. ¼ с Б. ½ с В. 2 с Г. 4 с
Яким виразом визначається частота коливань математичного маятника?
А. Б. В. Г.
Який приблизно період коливань математичного маятника довжиною 90 м? Прийняти прискорення вільного падіння g = 10 м/с2.
А. 1/18 з Б. 1/3 с. В. 3 с. Г. 18 с.
Як зміниться період коливань математичного маятника, якщо його довжину збільшили в 9 разів?
А. Збільшиться в 3 рази Б. Збільшиться в 9 рази
В. Зменшиться в 3 рази Г. Зменшиться в 9 рази
Яке з перерахованих коливань є вільним? а) Коливання вантажу на пружині, після однократного його відхилення від положення рівноваги; б) Коливання дифузора гучномовця під час роботи приймача.
А. Тільки а) Б. а) і б) У. Тільки б) Г. Ні а), ні б)
Вантаж підвішений на нитці і відхилений від положення рівноваги так, що його висота над землею збільшилася на 20 см. Приблизно з якою швидкістю тіло буде проходити положення рівноваги при вільних коливаннях?
А. 1 м/с Б. 2 м/с В. 4 м/с Г. 20 м/с.
При вільних коливаннях вантажу на пружині максимальне значення його потенціальної енергії 10 Дж, максимальне значення кінетичної енергії 10 Дж. У яких межах змінюється повна механічна енергія вантажу і пружини?
А. Змінюється від 0 до 10 Дж Б. Змінюється від 0 до 20 Дж
В. Не змінюється і дорівнює 10 Дж Г. Не змінюється і дорівнює 20 Дж
Задачі для самостійного розв’язку.
1. Написати рівняння гармонічного коливального руху з амплітудою 5 см, якщо за 1 хв здійснюється 150 коливань і початкова фаза коливань рівна 45°.
2. Написати рівняння гармонічного коливального руху з амплітудою 0,1 см, періодом 4 с і початковою фазою рівною нулю.
3. Амплітуда гармонічних коливань 50 мм, період 4 с, а початкова фаза π/4. Знайти зміщення точки при t = 0 і t = 1,5 с. (Відповідь: 35,2 мм; 0)
4. Через який проміжок часу від початку руху точка, що здійснює гармонічні коливання, зміститься від положення рівноваги на половину амплітуди ? Період коливань 24 с, початкова фаза рівна нулю. (Відповідь: 2 с)
5. Початкова фаза гармонічних коливань рівна нулю. Через яку частинку періоду швидкість точки буде рівна половині її максимальної швидкості ? . (Відповідь: 1/6)
6. За який проміжок часу від початку руху точка, що здійснює коливальний рух за рівнянням х = 7sin0,5πt, проходить шлях від положення рівноваги до максимального зміщення ? . (Відповідь: 1 с)
7. Амплітуда гармонічного коливання 5 см, період 4 с. Визначити максимальну швидкість і максимальне прискорення. . (Відповідь: 7,85 см/с; 12,3 см/с )
8.
Рівняння руху точки
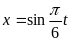 .
Визначити моменти часу, в які досягають
максимального значення швидкість і
прискорення. (Відповідь: 0, 6, 12 с; 3, 9, 15 с)
.
Визначити моменти часу, в які досягають
максимального значення швидкість і
прискорення. (Відповідь: 0, 6, 12 с; 3, 9, 15 с)
9.
Рівняння руху точки дано у вигляді
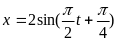 см.
Визначити : 1) період ; 2) максимальну
швидкість ; 3) максимальне прискорення.
(Відповідь: 4 с; 3,14 см/с; 4,93 см/с
)
см.
Визначити : 1) період ; 2) максимальну
швидкість ; 3) максимальне прискорення.
(Відповідь: 4 с; 3,14 см/с; 4,93 см/с
)
10. Точка здійснює гармонічні коливання. Період коливання 2 с, амплітуда 50 мм, початкова фаза рівна нулю. Визначити швидкість точки в той момент, коли зміщення від положення рівноваги 25 мм. (Відповідь: 13,6 см/с)
11. Написати рівняння гармонічного коливального руху, якщо максимальне прискорення точки 49,4 см/с², період коливань 2 с, а зміщення точки від положення рівноваги в початковий момент 25 мм.
12. Початкова фаза гармонічного коливання рівна нулю. При зміщенні точки від положення рівноваги 2,4 см її швидкість 3 см/с, а при зміщенні 2,8 см швидкість 2 см/с. Визначити амплітуду і період цього коливання. (Відповідь: 3,1 см; 4,1 с)
13. Визначити відношення кінетичної енергії точки, що коливається, до її потенціальної енергії для моментів часу: 1) T/12, 2) T/8, 3) T/6. Початкова фаза коливань рівна нулю. (Відповідь: 3, 1, 1/3)
14. На яку частину довжини потрібно зменшити довжину математичного маятника, щоб період коливань його на висоті 10 км був рівний періоду коливань на поверхні Землі ? (Відповідь: 0,003)
15. Визначити на скільки відстане маятниковий годинник за добу, якщо його підняти на висоту 5 км над поверхнею Землі. (Відповідь: 67,5 с)
16. Визначити період коливань математичного маятника довжиною L, підвішеного в вагоні, що рухається горизонтально з прискоренням а.
17. Визначити частоту гармонічного коливання, якщо відомі амплітуди зміщення і швидкості.
18. Визначити частоту гармонічного коливання і амплітуду зміщення, якщо відомі амплітуда швидкості і амплітуда прискорення.
19. Визначити відношення кінетичної енергії точки, що здійснює гармонічні коливання, до її потенціальної енергії, якщо зміщення точки від положення рівноваги складає: 1) х = А/4, 2) х=А/2, 3) х = А, де А – амплітуда коливань. (Відповідь: 15, 3, 0)
20.
Повна енергія тіла, що здійснює гармонічні
коливання, рівна 3
10ˉ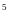 Дж, максимальна сила, що діє на тіло 1,5
мН. Написати рівняння руху цього тіла,
якщо період коливань 2 с, а початкова
фаза 60˚.
Дж, максимальна сила, що діє на тіло 1,5
мН. Написати рівняння руху цього тіла,
якщо період коливань 2 с, а початкова
фаза 60˚.
21. Амплітуда гармонічних коливань матеріальної точки 2 см, повна енергія
0,3 мкДж. При якому зміщенні від положення рівноваги на точку діє сила 22,5 мН ? (Відповідь: 1,5 см)
22. До пружини прикріплено вантаж масою 10 кг. Знаючи, що пружина під дією сили 1 Н розтягується на 1,5 см, визначити період вертикальних коливань. (Відповідь: 0,78 с)
23. До пружини прикріплено вантаж. Знаючи, що максимальна кінетична енергія коливань вантажу 1Дж, визначити коефіцієнт пружності пружини. Амплітуда коливань 5 см. (Відповідь: 805 Н/м)
24. Мідна кулька, підвішена на пружині, здійснює вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісили замість мідної кульки алюмінієву такого ж радіуса ?
25. До пружини підвішено шальку вагів з гирями. При цьому період вертикальних коливань 0,5 с. Після того як на шальку поклали ще додаткові гирі, період вертикальних коливань став 0,6 с. На скільки видовжилась пружина від додаткових гир ? (Відповідь:
2,7 см)
26. Написати рівняння руху, отриманого в результаті додавання двох однаково направлених гармонічних коливань з однаковим періодом 8 с і однаковою амплітудою 2 см. Різниця фаз цих коливань π /4. Початкова фаза одного з коливань рівна нулю.
27.
Визначити амплітуду і початкову фазу
гармонічного коливання, отриманого від
додавання однаково направлених коливань,
даних рівняннями х
= 0,02sin(5πt
+ π/2)
і х
=0,03sin
(5πt
+ π/4).
(Відповідь:
4,6 см; 62
 )
)
28.
В результаті додавання двох однаково
направлених гармонічних коливань з
однаковими амплітудами і однаковими
періодами отримують результуюче
коливання з тим же періодом і частотою.
Визначити різницю фаз коливань доданків.
(Відповідь: 2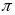 /3)
/3)
29. 1) Визначити амплітуду і початкову фазу гармонічного коливання, отриманого від додавання однаково направлених коливань, даних рівняннями: х = 4sin πt см, х = 3 sin (πt + π/2) см. 2) Написати рівняння результуючого коливання. 3) Дати векторну діаграму додавання амплітуд. (Відповідь: 5 см; 0,2 )
30. Період затухаючих коливань 4 с, логарифмічний декремент затухання 1,6, початкова фаза – нуль. Зміщення точки при t = T/4 – 4,5 см. Написати рівняння руху цього коливання.
31.
Рівняння
затухаючих коливань дано у вигляді х =
5е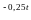 sin
sin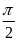 t
м. Визначити швидкість точки в моменти
часу: 0, T,
2T,
3T
і 4Т. (Відповідь: 7,8 м/с; 2,88 м/с; 1,06 м/с;
t
м. Визначити швидкість точки в моменти
часу: 0, T,
2T,
3T
і 4Т. (Відповідь: 7,8 м/с; 2,88 м/с; 1,06 м/с;
0,39 м/с; 0,14 м/с)\
32. Логарифмічний декремент затухання математичного маятника 0,2. Визначити, у скільки разів зменшиться амплітуда коливань за одне повне коливання маятника. (Відповідь: 1,22)
33. Визначити логарифмічний декремент затухання математичного маятника, якщо за 1хв амплітуда коливань зменшилась в 2 рази. Довжина маятника 1 м. (Відповідь: 0,023)
34. Математичний маятник довжиною 24,7 см здійснює затухаючі коливання. Через який проміжок часу енергія коливань маятника зменшиться в 94 рази ? Логарифмічний декремент затухання : 1) 0,01, 2) 1. (Відповідь: 120 с; 1,22 с)
35. Амплітуда затухаючих коливань математичного маятника за 1 хв. зменшилось вдвічі. У скільки разів вона зменшилась за 3 хв. ? (Відповідь: 8)
36. Математичний маятник довжиною 0,5 м, виведений з положення рівноваги, відхилиться при першому коливанні на 5 см, а при другому (в той же бік) – на 4 см. Визначити час релаксації. (Відповідь: 6,4 с)
37. За 10 с амплітуда коливань зменшилась у 10 разів. За який проміжок часу вона зменшиться в 100 разів. (Відповідь: 20 с)
38.
За 16,1 с амплітуда коливань зменшилась
в 5 разів. Визначити коефіцієнт затухання
і час релаксації. (Відповідь: 0,1 с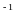 ;
10 с)
;
10 с)
39.
За час релаксації рівний 100 с система
здійснює 100 коливань. Визначити коефіцієнт
затухання, логарифмічний декремент
затухання, добротність системи.
(Відповідь: 10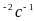 ;
10
;
10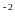 ;
314; 2
;
314; 2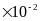 )
)
40. За час, протягом якого система здійснює 100 коливань, амплітуда зменшується в 5 разів. Визначити добротність системи. (Відповідь: 195)
41. Добротність коливальної системи 2, а частота вільних коливань 100 Гц. Визначити власну частоту коливань системи. (Відповідь: 103 с )
42. Частота вільних коливань системи 100 Гц, резонансна частота 99 Гц. Визначити добротність системи. (Відповідь: 4)
43. Осцилятор з часом релаксації 20 с в момент t = 0 має початкове зміщення 10 см. При якому значенні початкової швидкості це зміщення буде рівне амплітуді ?(Відповідь:-0,5 см/с)
44. Точка здійснює затухаючі коливання з частотою 25 сˉ¹. Визначити коефіцієнти затухання, якщо в початковий момент швидкість точки рівна нулю, а зміщення від положення рівноваги в 1,02 рази менше амплітуди. (Відповідь: 5 с )
ДОМАШНЄ ЗАВДАННЯ: розв’язати задачі.
1 Визначите період гармонічних коливань математичного маятника, що робить одне повне коливання за 2 с, якщо прискорення вільного падіння становить 9,81 м/с2. У скільки разів потрібно змінити довжину маятника, щоб частота його коливань збільшилася в 2 рази?
2 У скільки разів період коливань математичного маятника на Місяці відрізняється від періоду коливань того ж маятника на Землі (прискорення вільного падіння на Місяці в 6 разів менше, ніж на Землі)?
3 Вантаж масою m коливається на пружині твердістю k з амплітудою А. Знайдіть: 1) повну механічну енергію Е; 2) швидкість проходження точкою А.
ВИКЛАДАЧ – Марінець І.С.
