2. Нелинейные методы выделения границ областей

Градиентный фильтр. В обработке изображений первые производные реализуются через модуль градиента. Для функции f(х, у) градиент в точке (х, у) определяется как двумерный вектор-столбец:

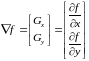
Модуль этого вектора определяется следующим образом:

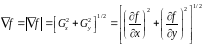(2.4)

Компоненты вектора градиента являются линейными операторами, но модуль вектора, очевидно, нет, поскольку он выражается через операции возведения в квадрат и извлечения квадратного корня. Хотя это и не является строго правильным, модуль вектора градиента часто называют градиентом.

Объем вычислений, необходимых для обработки всего изображения оператором (2.4), достаточно велик, поэтому частой практикой является замена значения модуля градиента суммой модулей отдельных компонентов, вместо квадратов и квадратных корней:

(2.5)

Аналогично лапласиану, первоначально определим дискретные приближения приведенных выше уравнений, а затем уже по ним будут сформированы соответствующие маски фильтров. Чтобы упростить последующие рассуждения, для указания точек в окрестности 3×3 будут использоваться обозначения, показанные на рис. 2.15.

Рис. 2.15. Область изображения размерами 3х3 элемента (z₁…z₉ – значения яркости соответствующих пикселей под маской) и маски, используемые для вычисления градиента в точке, отмеченной z₅. Суммы коэффициентов по каждой из масок равны нулю

Так, например, центральная точка z₅ обозначается f(x, у), а z1 обозначается f(x-1, у-1), и так далее.

Фильтр Робертса.

Простейшими приближениями первой производной являются

G_x = (Z₈ — Z₅) и G_y = (Z₆ – Z₅).

Два других определения, предложенные Робертсом, используют перекрестные направления:

G_x=(Z₉ – Z₅) и G_y=(Z₈ – Z₆).

Если выбрать уравнение (2.4), то градиент будет вычисляться по следующей формуле:

Если используются абсолютные значения, тогда получим следующее приближение к значениям градиента:

Это уравнение может быть реализовано с помощью двух масок (Рис.2.16, а,б).

Рис. 2.16. Маски фильтра Робертса

Эти маски называют перекрестным градиентным оператором Робертса.

Фильтр Собеля.

Маски четного размера реализовывать неудобно. Наименьшая маска фильтра, которая нас интересует, имеет размеры 3×3. Приближением, использующим абсолютные значения для той же самой точки Z₅, но уже по маске 3x3, будет

(2.6)

Разность между значениями пикселей в третьей и первой строках окрестности 3x3 приближает значение производной по направлению х, а разность между значениями пикселей в третьем и первом столбцах приближает значение производной по направлению у. Маски на рис. 2.15, б, в называют оператором Собеля (Sobel). Они могут использоваться для реализации уравнения (2.6). Заметим, что суммы коэффициентов каждой из масок равны 0, и это означает, что на участках изображения с постоянным уровнем яркости отклик любого из приведенных операторов будет равен 0, как и должно быть у оператора, соответствующего первой производной.

Оператор Превита

Оператор Превита действует аналогично оператору Собеля и также рассматривает два ядра свертки:

,

Исходя из этих сверток, вычисляются величина и направление края. Свертка для каждой функции ядра вычисляется отдельно. Обозначим отклики ядер Hx и Hy соответственно:

, ,

где А – соответствующий фрагмент обрабатываемого изображения. В качестве отклика данного фильтра выступает величина .