Р ешение

На рис. 1.13,6 показаны силы, действующие на рычаг АВ. Как известно, рычаг находится в равнове­сии, если сумма мо­ментов всех действу­ющих на него сил относительно точки вращения рычага (в рассматриваемом примере — точки А) равна нулю:

Откуда

Пример 6. Определить опорные реакции бал­ки, показанной на рис. 1.14, а.

Решение

Р ассмотрим равновесие балки АВ, к которой приложены как заданные, так и искомые силы. Освобож­даем балку от связей и заменяем их действие реакциями (рис. 1.14,6). Получили плоскую систему сил.

Выбираем систему ко­ординат (см. рис. 1.14,6).

Составляем три уравне­ния равновесия:

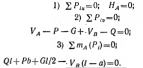
Решая второе и третье уравнения, получаем:

С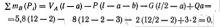 оставим провероч­ное уравнение

следовательно, опорные реакции определены вер­но.

Пример 7. Для заданной балки (рис. 1.15, а) оп­ределить опорные реакции.

Р ешение

Рассмотрим равновесие балки АВ, к которой приложены все заданные и искомые силы. Освободим балку от связей и заменим их действие реакциями (рис. 1.15, б). Получили плоскую систему произвольно расположенных сил.

Выбираем систему координат (см. рис. 1.15, 6). Для полученной системы сил в рассматриваемом примере целе­сообразно составить следующие три уравнения равнове­сия:

В этом случае в каждое уравнение равновесия войдет только одна искомая реакция:

г де l cos α — плечо силы R_B относительно точки А. Подставляя числовые значения, находим

При определении опорных реакций не было использовано уравнение равновесия ΣP_iv = 0. Если реакции определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем

следовательно, реакции определены верно.

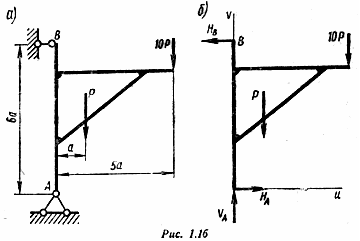
Пример 8. Для плоской рамы (рис. 1.16,а) определить опорные реакции.

Решение

О свобождаем раму от связей и заменяем их действие реакциями Н_А, Нв и V_A. Действующие на раму нагрузки и искомые реакции показаны на рис. 1.16, б. Получили плоскую систему произвольно расположенных сил. Выбираем систему координат (см. рис. 1.16, б) и составляем уравнения равновесия:

Искомые реакции получились положительными; это указывает на то, что предварительно выбранные направ­ления реакций совпадают с действительными.

В качестве проверочного уравнения берем ΣР_tu = 0, так как оно не было использовано для определения опорных реакций.

Проектируя все силы на ось и, получаем

следовательно, реакции опре­делены верно.

Контрольные вопросы и задания

1. Какие силы из системы сил (рис. 4.8) образуют пары?

F₁=F₂ = F₄; F₃ = F₆; F₅ = 0,9F₆.

2. О пределите момент изображенной на рис. 4.9 пары сил. \F\ = \F'\ = 5кН.

2. Какие из изображенных пар (рис. 4.10) эквивалентны, если

F ₁ = F2 = 8 кН; F3 = 6,4 кН; а₁ = 2 м; а₂ = 2,5 м?

4. Какую силу необходимо приложить в точке с (рис. 4.11), что­бы алгебраическая сумма моментов относительно точки О была рав­на нулю?

OA = АВ = ВС = 5 м; F₁ = 7,8кН; F₂ = 3 кН.

5. Ответьте на вопросы тестового задания.

Т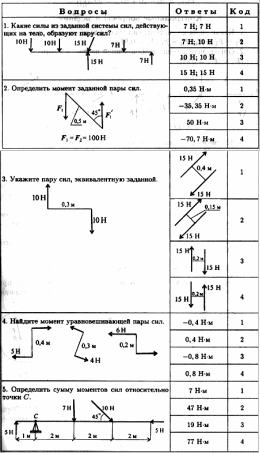 ема 1.3. Статика

ЛЕКЦИЯ 5

Тема 1.4. Плоская система произвольно расположенных сил

Иметь представление о главном векторе, главном моменте, равнодействующей плоской системы произвольно расположенных сил.

Знать теорему Пуансо о приведении силы к точке, приведение произвольной плоской системы сил к точке, три формы уравнений равновесия.

Уметь заменять произвольную плоскую систему сил одной си­лой и одной парой.

Теорема Пуансо о параллельном переносе сил

С илу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.

Дано: сила в точке А (рис. 5.1).

Добавим в точке В уравновешенную систему сил (F¹; F"). Обра­зуется пара сил (F¹, F"). Получим силу в точке В и момент пары т.

Приведение к точке плоской системы произвольно расположенных сил

Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему сле­дует упростить. Для этого все силы системы переносят в одну произ­вольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил.

Появившиеся при переносе пары называют присоединенными па­рами.

Д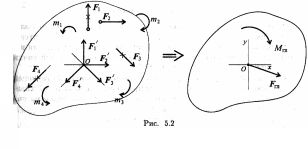 ана плоская система произвольно расположенных сил (рис. 5.2).

Переносим все силы в точку О. Получим пучок сил в точке О, который можно заменить одной силой — главным вектором систе­мы.

О бразующуюся систему пар сил можно заменить одной эквива­лентной парой — главным моментом системы.

Г лавный вектор равен геометрической сумме векторов произ­вольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.

По величине проекций главного вектора на оси координат нахо­дим модуль главного вектора:

Главный момент системы сил равен алгебраической сумме мо­ментов сил системы относительно точки приведения.

Таким образом, произвольная плоская система сил приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).