Таким образом, матрицы можно сравнивать, складывать, вычитать, умножать на любое число или друг на друга, транспонировать. Заметим, что делить матрицы нельзя. Ранг матрицы

В прямоугольной матрице А размера m  n вычеркиванием каких-либо строк и столбцов можно получить квадратные подматрицы k–го порядка, где k ≤ min (m; n). Определители таких подматриц называются минорами k–го порядка матрицы А.

Например, из матрицы А_3x4 можно получить подматрицы первого, второго и третьего порядков.

Количество N миноров k–го порядка матрицы А размера m  n можно вычислить по формуле:

,

где n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Ранг матрицы А обозначается rang A, или r(A), или r_А.

Из определения следует:

1) ранг матрицы А _{m x n} не превосходит меньшего из её размеров, т.е. rang A ≤ min (m; n);

2) rang A = 0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А = 0;

3) для квадратной матрицы n-го порядка rang A = n тогда и только тогда, когда матрица А – невырожденная.

Пример. Вычислите ранг матрицы

Решение. Матрица А имеет размер 35, поэтому r(A) ≤ min (3;5) = 3. Проверим, равен ли ранг трём, для этого вычислим миноры

третьего порядка, т.е. определители всех подматриц третьего порядка:

Заметим, что для указанной матрицы А миноров третьего порядка существует 10 (они получаются вычёркиванием произвольных двух столбцов матрицы). В данном случае нет необходимости вычислять их все, поскольку уже получен один ненулевой минор третьего порядка.

Пример. Вычислите ранг матрицы

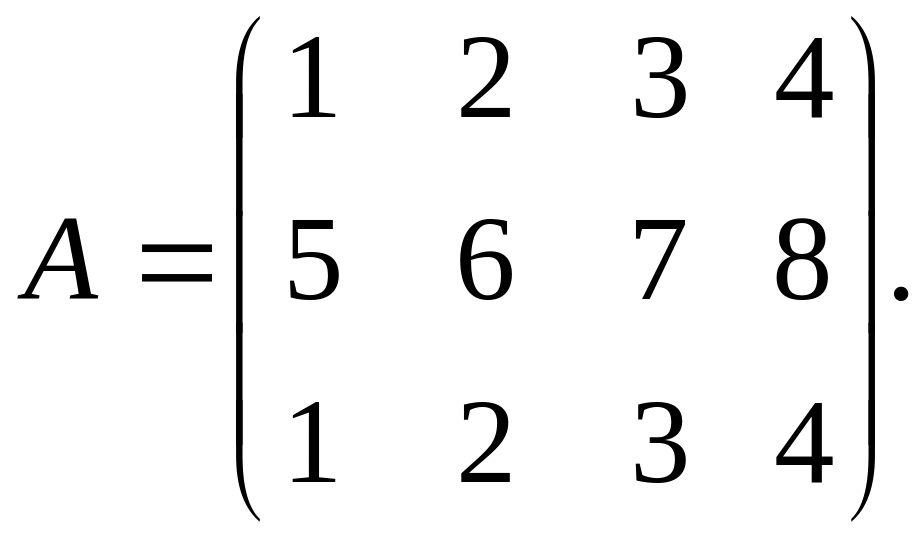
Решение. Матрица А имеет размер 34, поэтому r(A) ≤ min (3; 4) = 3. Проверим, равен ли ранг трём, для этого вычислим миноры третьего порядка.

Поскольку в матрице А равны первая и третья строки, то все оп­ределители третьего порядка (они получаются вычёркиванием одного из столбцов матрицы) равны 0, следовательно r(A) ≠ 3 r(A) ≤ 2.

Проверим, равен ли ранг 2, для этого вычислим миноры второго порядка. Их всего 18, но уже первый из них ненулевой:

Из приведённых примеров видно, что вычисление ранга мат­рицы перебором всех миноров - трудоёмкое занятие. Для облегчения данной задачи используют элементарные преобразования, сохра­няющие ранг матрицы. Это:

• отбрасывание нулевой строки;

• умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

• перестановка местами строк (столбцов) матрицы;

• прибавление к каждому элементу одной строки (столбца) соот­ветствующих элементов другой строки (столбца), умно­женных на любое число;

• транспонирование матрицы.

Теорема. Ранг матрицы не меняется при элементарных преобра­зованиях матрицы.

Доказательство теоремы следует из определения ранга матрицы и свойств определителей.

С помощью элементарных преобразований можно привести матрицу к треугольному или ступенчатому виду, тогда вычисление ранга не представляет труда.

Для ступенчатой матрицы

(a_ii ≠ 0, i = 1, 2, …, r; r ≤ n)

ранг равен r, т.к. существует минор r –го порядка, не равный нулю:

Пример. Вычислите ранг матрицы

Решение. Матрица А имеет размер 45, поэтому r(A) ≤ min (4;5) = 4. С помощью элементарных преобразований приведём матрицу к ступенчатому виду.

1) Поменяем местами 1-ю и 2-ю строки матрицы, чтобы элемент a₁₁ ≠ 0:

2) К элементам 3-й строки прибавим элементы 1-й строки, умноженной на 2, а к элементам 4-й строки просто прибавим элементы 1-й строки. Получим, что все элементы 1-го столбца, кроме a₁₁ = 2, равны 0:

3) Так как получились две одинаковые строки, то вычтем, например, из 4-й строки 3-ю. Затем отбросим нулевую 4-ю строку:

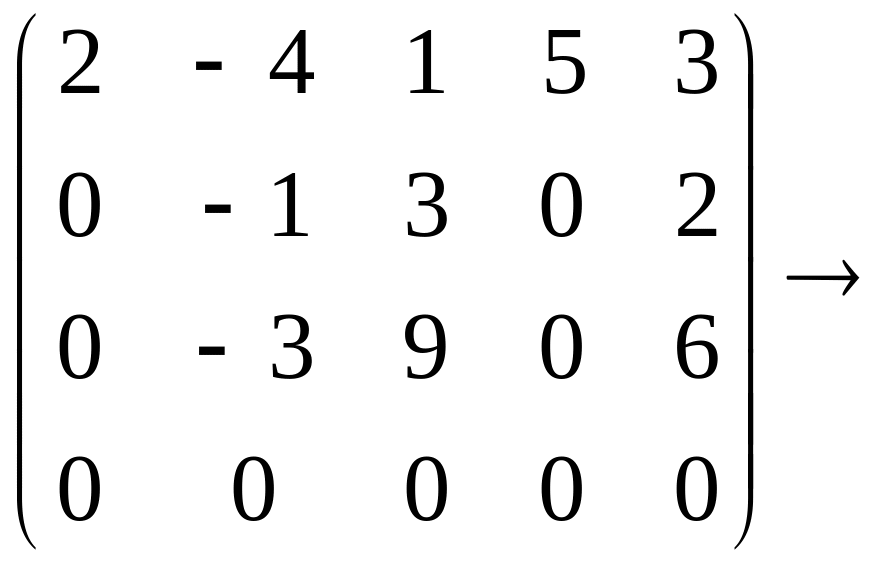
4) В полученной матрице размера 3  5 вторая и третья строки пропорциональны, поэтому к 3-й строке прибавим 2-ю, умноженную на (- 3). Опять получим нулевую строку, отбросим её:

Последняя матрица имеет ступенчатый вид, её размер 2  5, следовательно, её ранг, а значит и ранг исходной матрицы А, равен 2.

Понятие ранга матрицы связано с понятием линейной зависимости её строк или столбцов.

Рассмотрим произвольную матрицу А размера m  n. Обозначим её строки следующим образом:

…,

Две строки матрицы называются равными, если равны их соответствующие элементы, т.е.

Арифметические операции над строками матрицы (умножение строки на число, сложение строк) рассматривают как операции, проводимые поэлементно:

Строка е называется линейной комбинацией строк матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:

где - любые числа.

Строки матрицы называются линейно зависимыми, если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

= 0, (1)

где 0 = (0 0 … 0).

Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

Строки матрицы называются линейно независимыми, если линейная комбинация строк (1) равна нулю тогда и только тогда, когда коэффициенты = 0.

Аналогично определяются понятия линейной зависимости (независимости) столбцов.

Пусть ранг матрицы А равен r, тогда любой минор r–го порядка (r ≠ 0) называется базисным, а его столбцы и строки – базисными.

Рассмотрим две основные теоремы, которые имеют важное значение при исследовании систем линейных уравнений.

Теорема о базисном миноре. Любая строка (столбец) матрицы является линейной комбинацией её базисных строк (столбцов).

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу её линейно независимых строк (столбцов), через которые линейно выражаются все остальные её строки (столбцы).