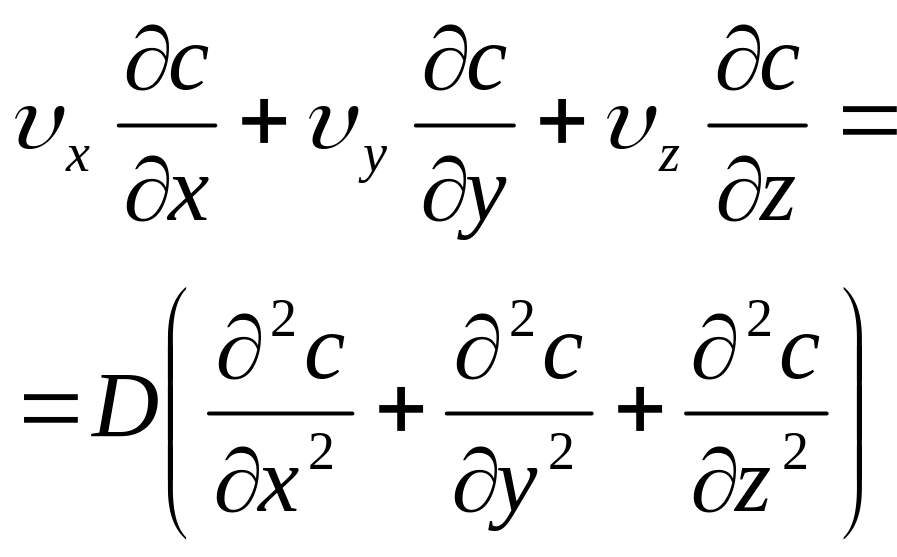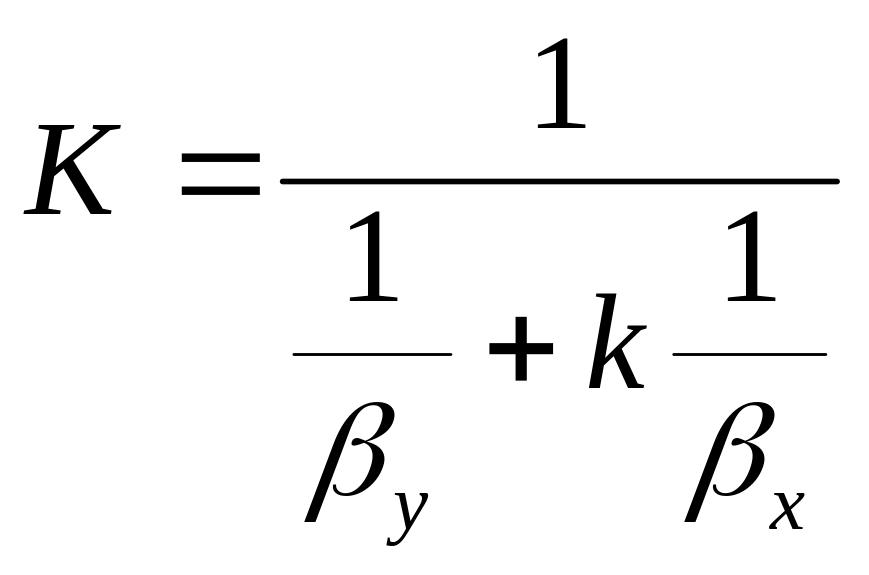- •Модуль 1. Класифікація процесів та їх рушійні сили
- •Тема 1. Поняття про виробничий і технологічний процеси та компоненти хімічного виробництва
- •Тема 2. Класифікація типових процесів
- •Безперервні процеси порівняно з періодичними мають ряд істотних переваг:
- •Тема 3. Моделювання та оптимізація процесів і апаратів
- •Тема 4. Аналітичні методи складання математичного опису виробничих об’єктів
- •1. Рівняння швидкості хімічного перетворення речовин
- •2. Рівняння гідродинаміки рідких і газоподібних середовищ
- •3. Процеси теплопереносу
- •4. Кінетика масопередачі
- •5. Аналітичне складання рівнянь статики й динаміки
- •Запитання для самоконтролю
- •Тема 1. Процеси переміщення та їх апаратна реалізація.
- •Таким чином, в задачах управління можна виділити змінні, що визначають процес витікання сипких матеріалів з отворів в ємностях.
- •2. Переміщення сипких матеріалів за допомогою пневмотранспорту|
- •3. Апаратна реалізація механічних процесів. Переміщення
- •Тема 2. Процеси подрібнення та їх апаратна реалізація
- •1. Фізико-хімічні основи процесів подрібнення твердих матеріалів
- •2. Апаратна реалізація механічних процесів. Подрібнення
- •Тема 3. Процеси класифікації. Технологічний розрахунок барабанного класифікатора зернистих матеріалів
- •Запитання для самоконтролю
- •Модуль 3. Гідромеханічні процеси та їх апаратна реалізація
- •Тема 1. Класифікація неоднорідних систем і методів їх розділення
- •Тема 2. Фізико-хімічні основи процесу відстоювання та їх апаратна реалізація
- •1. Апаратна реалізація процесу відстоювання
- •2. Розрахунок горизонтальних відстійників. Закономірності відкладень осаду та формування освітленої зони
- •3. Порівняльна характеристика управління процесами відстоювання Управління процесом протитечійного відстоювання
- •Регулювання зміни витрати суспензії
- •Регулювання подачі коагулянту
- •Регулювання режиму роботи гребкового механізму
- •Управління відстійниками періодичної дії
- •Тема 3. Фізико-хімічні основи фільтрування та їх апаратна реалізація
- •1. Апаратна реалізація процесу фільтрування
- •Тема 4. Фізико-хімічні основи мембранних методів розділення та математичне моделювання процесів ультрафільтрування
- •1. Класифікація і математичне моделювання режимів ультрафільтрування
- •Запитання для самоконтролю
- •Модуль 4. Теплові процеси та їх апаратна реалізація
- •Тема 1. Процеси теплообміну та їх апаратна реалізація
- •1. Фізико-хімічні основи теплопередачі
- •2. Математична модель процесу із|із| зосередженими параметрами
- •3. Апаратна реалізація процесів теплообміну
- •Тема 2. Процеси випаровування та їх апаратна реалізація
- •1. Фізико-хімічні основи процесу випаровування
- •2. Методика розрахунку випарних апаратів
- •3. Математичне моделювання та розрахунок однокорпусного випарного апарату
- •4. Робота випарної установки
- •5. Апаратна реалізація процесів випаровування
- •6. Контактне випаровування
- •Тема 3. Процеси спалювання та їх апаратна реалізація
- •1. Фізико-хімічні основи процесу спалювання (процес горіння)
- •2. Оптимальні умови спалювання. Регулювання витрати палива і повітря
- •3. Апаратна реалізація процесу спалювання (Промислові реактори для системи газ-тверда речовина)
- •Запитання для самоконтролю
- •Модуль 5. Процеси масообміну та їх апаратна реалізація
- •Тема 1. Загальні відомості про масообмінні процеси
- •Матеріальний баланс. Фактичний вихід продукту для гетерогенного процесу
- •2. Фізико-хімічні основи процесу масопередачі
- •3. Молекулярна та конвективна дифузія
- •4. Рівноваги між фазами. Закон Генрі для процесів адсорбції, хемосорбції, десорбції
- •Тема 2. Фізико-хімічні основи адсорбції та їх апаратна реалізація
- •1. Фазова рівновага. Типи ізотерм адсорбції
- •2. Типи ізотерм адсорбції
- •3. Активність адсорбенту
- •4. Методи адсорбції і десорбції
- •5. Розрахунок адсорбції у процесах осушки (очищення) газових потоків
- •7. Будова йонообмінних апаратів та установок
- •Тема 3. Фізико-хімічні основи процесів абсорбції та їх апаратна реалізація
- •1. Моделювання абсорбційно-десорбційних процесів
- •2. Апаратна реалізація процесів абсорбції
- •Запитання для самоконтролю
- •Модуль 6. Основні компоненти сировини, готової продукції та контроль якості сировини
- •Тема 1. Основні компоненти сировини та готового продукту
- •1. Принципи збагачення сировини
- •Тема 2. Контроль якості сировини
- •1. Контроль якості продукції, різновиди контролю
- •2. Методи визначення показників якості продукції
- •Запитання для самоконтролю
- •Модуль 7. Технологічні схеми галузевих виробництв
- •Тема 1. Основи розрахунків виробничих процесів
- •4. Математичне моделювання процесів масо- і тепловіддачі в газовій фазі насадочних колон
- •Тема 2. Технологія неорганічних речовин. Загальні положення хімічної технології Хімія і навколишнє середовище
- •Хімія, психологія і навколишнє середовище
- •Новий стиль діяльності
- •Нові ресурсозберігаючі безвідходні технології
- •1. Ресурсозберігаюча біциклічна схема виробництва амоніаку
- •2. Отримання рідких комплексних добрив на основі переробки екстракційної фосфатної кислоти
- •3. Нітратні добрива
- •Виробництво амоніачної селітри, карбаміду та амоній сульфату
- •Складнi (комплекснi) добрива
- •Нiтроамофоска
- •Тема 3. Технологія органічних речовин
- •1. Продукти і сировина промислового органічного синтезу
- •2. Основні процеси та реакції органічного синтезу
- •3. Технологія полімерів. Виробництво хімічних волокон
- •4. Технологія одержання напівпродуктів для синтетичних волокон
- •5. Виробництво віскози, капрону, найлону
- •Поліамідне волокно капрон
- •Волокна найлон
- •Тема 4. Основні відомості про виробничі процеси одержання цукру
- •1. Основні відомості про цукор та сировину,
- •З якої його виробляють
- •2. Технологічна схема виробництва розсипного цукру
- •3. Технологічні системи виробництва кускового цукру
- •Тема 5. Переробка відходів та очищення стічних вод
- •Замкнуті системи водного господарства гальванічних виробництв
- •2. Метод зворотного осмосу, ультрафільтрація для очищення стічних вод
- •Запитання для самоконтролю
- •Модудь 8. Задачі діагностування стану технологічних процесів і технічний контроль
- •Тема 1. Актуальні задачі діагностування
- •1. Цілі та об’єкти виявлення й діагностики несправностей
- •2. Види несправностей і ймовірності їх появи
- •3. Проектування систем виявлення і діагностики несправностей
- •4. Техніка виявлення і діагностики несправностей
- •Діагностика несправностей
- •5. Випробування, які можуть бути проведені для виявлення і діагностики несправностей
- •6. Усунення несправностей
- •7. Діагностика хімічних реакторів на основі аналізу гідродинамічних шумів
- •Тема 2. Методи контролю стану обладнання і перебігу процесів
- •1. Формулювання задач оптимізації
- •2. Методи термодинамічного аналізу і оптимізація технологічних процесів
- •Подібність в підходах
- •Відмінність підходів
- •Запитання для самоконтролю
- •Vі. Контрольна тестова програма Тести поточного контролю Модуль 1. Класифікація процесів та їх рушійні сили
- •Модуль 2. Механічні процеси та їх апаратна реалізація
- •Модуль 3. Гідромеханічні процеси та їх апаратна реалізація
- •Модуль 4. Теплові процеси та їх апаратна реалізація
- •Модуль 5. Процеси масообміну та їх апаратна реалізація
- •1. Видами процесів масопередачі між фазами є:
- •2. Абсорбція – поглинання газів або пари з газових або паро- газових сумішей:
- •3. Закон Генрі:
- •10. Йонний обмін – це:
- •Модуль 6. Основні компоненти сировини, готової продукції та контроль якості сировини
- •2. Визначте принцип збагачення сировини:
- •Модуль 7. Технологічні схеми галузевих виробництв
- •Модуль 8. Задачі діагностування технологічних процесів і технічний контроль
- •7. Кластерний аналіз відноситься до категорії:
- •8. Більшість задач в технічній діагностиці хімічного обладнання можна вирішити шляхом:
- •9. Ексергією називається:
- •10. Методологічні підходи термодинаміного аналізу мають загальну основу:
- •Тести підсумкового контролю
- •11. Відстоювання – це процес:
- •12. Гідравлічну крупність визначають:
- •14. Позначте оптимальні технічні показники випарних апаратів:
- •16. Основне рівняння теплопередачі має вигляд:
- •25. Емульсії – це:
- •32. Основними джерелами тепла в хімічній промисловості є:
- •33. Перевагою насиченої водяної пари як теплоносія при нагріванні є:
- •34. Видами процесів масопередачі між фазами є:
- •Паливо – це:
- •79. Закон Генрі:
- •84. Екстракція – це:
- •90. Адсорбція – це:
- •91. Визначити правильне позначення формулювання задачі оптимізації:
- •92. Визначити принцип збагачення сировини:
- •93. Розрахувати, яка кількість азоту та водню практично витрачається для виробництва 1 т амоніаку (вихід продукту 40%):
- •99. Визначити витрати сульфур(іv) оксиду на знекиснення води, що містить 3 мг о2 в 1 дм3. Продуктивність установки 100 м3/год:
- •VII. Тематика самостійної та індивідуальної роботи
- •VIII. Термінологічний словник
- •Iх. Література
- •Тема 3. Процеси спалювання та їх апаратна реалізація…………..161
- •Тема 1. Загальні відомості про масообмінні процеси.....................174
- •Тема 2. Фізико-хімічні основи адсорбції та їх апаратна реалізація..............................................................................................184
- •Тема 3. Фізико-хімічні основи процесів абсорбції та їх апаратна реалізація..............................................................................................202
- •Тема 1. Основні компоненти сировини та готового продукту.......214
- •Тема 2. Контроль якості сировини....................................................224
- •Тема 1. Основи розрахунків виробничих процесів.........................230
- •Тема 1. Актуальні задачі діагностування.........................................301
- •Тема 2. Методи котролю обладнання і перебігу прцесів………...323 1. Формування задач оптимізації.......................................................323
- •VII. Тематика самостійної та індивідуальної
- •Виробничі процеси та обладнання об’єктів автоматизації
- •33028, Рівне, вул. Соборна,11.
4. Кінетика масопередачі
Перерозподіл компонента між двома взаємодіючими фазами відбувається за рахунок процесів масопередачі.
Розглянемо
опис процесу масопередачі з рідкої фази
в парову для випадку ідеальної бінарної
суміші. Основні розрахункові співвідношення,
що описують цей процес, наведені в
таблиці
5. Умови термодинамічної рівноваги
полягають у рівності хімічних потенціалів
компонента в обох фазах системи. При
цьому встановлюються рівноважні значення
концентрацій
![]() і
cx
компонента
у фазах 1 і 2, які для бінарних систем
зв'язані при постійному тиску рівнянням
типу (1, а), наведеним у таблиці
5. При розгляді процесів ректифікації,
що протікають практично при постійному
тиску, за першу фазу приймається рідина
з концентрацією
cx,
в
якості другої фази –
пара з концентрацією компонента
.
Розділяючі
суміші можна розглядати як ідеальні та
неідеальні. Для бінарних ідеальних
систем співвідношення рівноважних
концентрацій
знаходиться за формулою (1, б) з таблиці
5. Коефіцієнт відносної леткості
компонентів аВ.Л.
дорівнює відношенню тиску насичених
парів більш леткого компонента до тиску
насичених парів менш леткого компоненту
(при однаковій температурі).
і
cx
компонента
у фазах 1 і 2, які для бінарних систем
зв'язані при постійному тиску рівнянням
типу (1, а), наведеним у таблиці
5. При розгляді процесів ректифікації,
що протікають практично при постійному
тиску, за першу фазу приймається рідина
з концентрацією
cx,
в
якості другої фази –
пара з концентрацією компонента
.
Розділяючі
суміші можна розглядати як ідеальні та
неідеальні. Для бінарних ідеальних
систем співвідношення рівноважних
концентрацій
знаходиться за формулою (1, б) з таблиці
5. Коефіцієнт відносної леткості
компонентів аВ.Л.
дорівнює відношенню тиску насичених
парів більш леткого компонента до тиску
насичених парів менш леткого компоненту
(при однаковій температурі).
Перенесення речовини в межах однієї фази здійснюється за рахунок молекулярної дифузії і конвективного переносу.
Таблиця 5
Рівняння для розрахунку процесу масопередачі
№ з/п |
Найменування рівнянь |
Рівняння |
1 |
2 |
3 |
1 |
Рівноважні співвідношення: а) загальний вигляд
б) для ідеальних бінарних сумішей |
|
2 |
Рівняння Фіка: а) диференціальна форма б) кінцева форма |
|
3 |
Рівняння Ньютона- Щукарьова (перенос маси від границі фази в ядро потоку) |
|
4 |
Рівняння конвективної дифузії (в стаціонарних умовах) |
|
продовження табл. 5
1 |
2 |
3 |
5 |
Основні рівняння масо- переносу з однієї фази в іншу: а) загальний вигляд рівняння
б) рівняння масопере-дачі в межах однієї фази від границі поділу в ядро потоку в) рівняння масопере-дачі при розрахунку за площею ефективного поперечного перерізу аппарата г) рівняння масопередачі при розрахунку за величиною об'єму апарату |
|
6 |
Граничні умови для процесу масопередачі з однієї фази в іншу |
|
7 |
Загальне критеріальне рівняння для розрахунку коефіцієнта масовіддачі з боку будь-якої фази |
|
8 |
Рівняння для розрахунку загального коефіцієнту масопередачі за коефіцієнтами масовіддачі |
|
Молекулярна дифузія здійснюється без видимого переміщення ділянок фази і обумовлена тепловим рухом молекул. Еквімолярне (при рівності числа молей компонентів, що переходять із однієї фази в іншу) перенесення речовини за рахунок молекулярної дифузії описується рівнянням Фіка (рівняння (2, а)в таблиці 5).
Потік
речовини
![]() пропорційний градієнту концентрації
∂c/∂δ
компонента
за шаром товщиною δ
і поверхні F.
Коефіцієнт
пропор-ційності D
називається
коефіцієнтом
молекулярної дифузії.
При сталості градієнта концентрації
рівняння Фіка приймає вигляд залежності
(2, б),
наведеної
в таблиці 5. Умова рівноваги при
молекулярній дифузії в межах однієї
фази відповідає рівності концентрацій
компонента у всіх точках.
пропорційний градієнту концентрації
∂c/∂δ
компонента
за шаром товщиною δ
і поверхні F.
Коефіцієнт
пропор-ційності D
називається
коефіцієнтом
молекулярної дифузії.
При сталості градієнта концентрації
рівняння Фіка приймає вигляд залежності
(2, б),
наведеної
в таблиці 5. Умова рівноваги при
молекулярній дифузії в межах однієї
фази відповідає рівності концентрацій
компонента у всіх точках.
У рухомій фазі перенесення речовини здійснюється також за рахунок конвекції, тобто шляхом відносного переміщення окремих ділянок потоку. Процес переносу компонента від границі до ядра фази характеризується рівнянням (3) з таблиці 5 (с-сГР – різниця концентрацій в ядрі і на границі). Коефіцієнт масовіддачі β у фазі є складною функцією сукупності параметрів. Фактично β є розв'язком системи рівнянь, що описує конвективний перенос компонента у фазі.
Конвективний масоперенос (аналогічно теплопереносу) в цілому описується системою, що складається з рівнянь Нав'є-Стокса і нерозривності потоку, рівняння конвективної дифузії компонента (другий закон Фіка), що є рівнянням матеріального балансу по компоненту для нескінченно малого об'єму в рухомому потоці, а також початкових і граничних умов.
Рівняння встановленої конвективної дифузії (залежність (4) в таблиці 5) – за формою цілком аналогічне рівнянню Фур'є-Кірхгофа для конвективного теплопереносу.
Залежність (6), наведена в таблиці 5, визначає граничні умови процесу при умові, що на границі фази існує дифузійний шар товщиною δ, перенесення речовини через який здійснюється тільки молекулярною дифузією (Δс – різниця концентрацій у ядрі потоку і на границі). Використання теорії подібності дозволяє і в цьому випадку визначити розв'язок системи рівнянь, що описують перенесення компонента в межах однієї фази, як функцію критеріїв (рівняння (7) в таблиці 5). У цьому рівнянні є дифузійні критерії подібності:
![]()
![]() (37)
(37)
При
розгляді масопередачі між двома
взаємодіючими фазами в системі пара-рідина
для розрахунку використовують формули
(7, а)
і
(7, б) з таблиці 5. У тому випадку, коли
поверхня поділу фаз не може бути
визначена, застосовують залежності (5,
в)
і
(5, г). У ці вирази входять величини:
![]() –
приведений коефіцієнт масопередачі
між двома фазами, розрахований на одиницю
площі FЕФ
ефективного
поперечного перерізу апарата;
–
приведений коефіцієнт масопередачі
між двома фазами, розрахований на одиницю
площі FЕФ
ефективного
поперечного перерізу апарата;
![]() –
приведений коефіцієнт масопередачі
між двома фазами, розрахований на одиницю
об'єму V
апарату;
K
–
коефіцієнт масопередачі, віднесений
до одиниці поверхні F
контакту
фаз; Δс
= с*-с
–
різниця між рівноважною і робочою
концентраціями в одній фазі (рушійна
сила процесу). Для парової фази маємо:
–
приведений коефіцієнт масопередачі
між двома фазами, розрахований на одиницю
об'єму V
апарату;
K
–
коефіцієнт масопередачі, віднесений
до одиниці поверхні F
контакту
фаз; Δс
= с*-с
–
різниця між рівноважною і робочою
концентраціями в одній фазі (рушійна
сила процесу). Для парової фази маємо:
![]() (38)
(38)
де Δс, су*, су – робоча й рівноважна концентрації компонента (остання відповідає робочій концентрації сХ у рідині).
Коефіцієнти масопередачі K, , можна виразити через коефіцієнти масовіддачі в паровій βУ і рідкій βХ фазах (рівняння (8) у таблиці 5). Ця залежність отримана при допущенні, що концентрації на границі фаз – рівноважні, а перенос через граничні шари здійснюється тільки молекулярною дифузією. Величина К залежить від тангенса k кута нахилу кривої рівноваги при концентрації сх (рівняння (1, а) в таблиці 5). Незважаючи на недостатню обґрунтованість прийнятих припущень, результати розрахунку за співвідношенням (8) добре узгоджуються з експериментальними даними.