Вопрос 21. Двойные интегралы, их геометрический смысл и свойства. Теорема о сведении двойного интеграла к повторному.

Если существует предел интегральной суммы, когда n стремится к к бесконечности таким образом , что max di стремится к нулю,который не зависит ни от способа разбиения области D на части,ни от выбора точек в них, то он называется двойным интегралом.

Геометрический смысл двойных интегралов: величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела.

Основные свойства двойного интеграла:

1.

2.

3.Если область D разбить линией на две област и D1 и D2 такие, что а пересечение D1 и D состоит лишь из линии, их разделяющей (см. рис. 6), то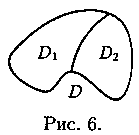

4. Если в области D имеет место неравенство ƒ(х;у) >=0, то и Если в области D функции ƒ(х; у) и (х; у) удовлетворяютнеравенству

5.

6. Если функция ƒ(х; у) непрерывна в замкнутой области D, площадь которой S, то где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.

7. Если функция ƒ(х;у) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (хо;уо), что

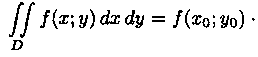
Величину называют средним значением функции ƒ(х;у) в области D.

Теорема о сведении двойного интеграла к повторному. Пусть функция f[x,y] определена и непрерывна в замкнутой, ограниченной, связной, квадрируемой области P. Пусть P обладает тем свойством, что любая вертикальная прямая x = α пересекает границу области P самое большее в двух точках, ординаты которых удовлетворяют неравенству (α) ≤ (α). Тогда справедлива следующая формула сведения двойного интеграла от функции f[x,y] по области P к повторному:

f[x,y]dS = dx f[x,y]dy

где a и b наименьшая и наибольшая абсциссы точек области P.

Вопрос 22. Замена переменных в двойном интеграле. Геометрические и физические приложения двойных интегралов.

Замена переменных в двойном интеграле описывается формулой

где выражение 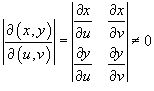представляет собой так называемый якобиан преобразования

Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1. Найти образ S в новой системе координат для исходной области интегрирования R;

2. Вычислить якобиан преобразования и записать дифференциал в новых переменных ;

3. Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки и .

1.Объем тела

Как уже показано (п. 7.2), объем цилиндрического тела находится по формуле

где z=ƒ(х;у) - уравнение поверхности, ограничивающей тело сверху.

2. Площадь плоской фигуры

Если положить в формуле (7.4) ƒ(х;у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н=1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

или, в полярных координатах,

3. Масса плоской фигуры

Как уже показано (п. 7.2), масса плоской пластинки D с переменной плотностью γ=γ(х;у) находится по формуле

4. Статические моменты и координаты центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей Ох и Оу (см. Часть 1, п. 41.6) могут быть вычислены по формулам

а координаты центра масс фигуры - по формулам

5. Моменты инерции плоской фигуры

Моментом инерции материальной точки массы м относительно оси l называется произведение массы м на квадрат расстояния d точки до оси, т. е. Мl=m • d2. Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат - по формуле Мо=Мх +Му