Методи знаходження оцінок

Метод моментів, запропонований К. Пірсоном.

У цьому методі визначена кількість вибіркових моментів (початкових чи центральних , або тих та інших) прирівнюється до відповідних

теоретичних моментів розподілу ( чи ) випадкової величини X.

, - дискретна випадкова величина з функцією ймовірностей ;

, - для неперервної випадкової величини з густиною ймовірностей , де .

◄ Приклад 2.1 Знайти оцінку методом моментів для параметра λ закону Пуассона.

Розв’язання. В даному випадку для знаходження єдиного параметра λ достатньо прирівняти теоретичний та емпіричний початкові моменти першого порядку. – математичне сподівання випадкової величини X. Для випадкової величини, розподіленої за законом Пуассона, . Момент _, згідно з формулою для початкових моментів, дорівнює . Звідси, оцінка методом моментів параметра λ закону Пуассона є вибіркове середнє .►

Оцінки методом моментів параметра зазвичай спроможні, однак за ефективністю вони не є «найкращими».

Метод максимальної правдоподібності, запропонований Р. Фішером.

Основу методу складає функція правдоподібності, що виражає густину ймовірностей (ймовірність) сумісної появи результатів вибірки :

, або

.

Згідно з методом максимальної правдоподібності в якості оцінки невідомого параметра θ приймається таке значення , яке максимізує функцію L.

Пошук оцінки спрощується, якщо максимізувати не саму функцію L, а , оскільки максимум обох функцій досягається при одному і тому

самому значенні θ. Тому , . Потім знаходимо точку максимума функції.

◄ Приклад 2.2 Знайти оцінку методом максимальної правдоподібності для ймовірності p настання деякої події A за даним числом m появи цієї події в n незалежних випробуваннях.

Розв’язання. Складемо функцію правдоподібності:

, або .

Тоді і , звідки . Можна показати, що при виконується достатня умова екстремуму функції L.

Таким чином, оцінкою методом максимальної правдоподібності ймовірності p події A буде частота цієї події.►

◄Приклад 2.3 Знайти оцінки методом максимальної правдоподібності для параметрів a і нормального розподілу за даними вибірки.

Розв’язання. Густина ймовірності нормально розподіленої випадкової величини . Тоді функція правдоподібності має вигляд:

.

Прологарифмуємо та отримаємо:

.

Для знаходження параметрів a і необхідно прирівняти до нуля частинні похідні по параметрах a і , тобто розв’язати систему рівнянь правдоподібності:

звідки оцінки максимальної правдоподібності рівні:

, .

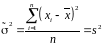Таким чином, оцінками методу максимальної правдоподібності математичного сподівання a і дисперсії нормально розподіленої випадкової величини є відповідно вибіркове середнє і вибіркова дисперсія .►

Важливість методу максимальної правдоподібності пов’язана із його оптимальними властивостями. Так, якщо для параметра θ існує ефективна оцінка , то оцінка максимальної правдоподібності єдина і рівна . Крім цього, при достатньо загальних умовах оцінки максимальної правдоподібності є спроможними, асимптотично незміщеними, асимптотично ефективними і мають нормальний розподіл.

Основний недолік методу максимальної правдоподібності – важкість обчислення оцінок.

Метод найменших квадратів – один із найбільш простих прийомів побудови оцінок. Він полягає у тому, що оцінка визначається з умови мінімізації суми квадратів відхилень вибіркових даних від шуканої оцінки.

◄Приклад 2.4 Знайти оцінку методом найменших квадратів для генерального середнього .

Розв’язання. Згідно із методом найменших квадратів знайдемо оцінку з умови мінімізації суми: Використовуючи необхідну умову екстремуму, прирівняємо до нуля похідну

, звідки і , тобто оцінка методом найменших квадратів генерального середнього є вибірковим середнім .►

Метод найменших квадратів , по-перше, не потребує знання закону розподілу вибіркових даних; по-друге, достатньо добре розроблений в плані обчислювальної реалізації.