7. Заключение

Анализ источников показал, что наиболее приоритетного вида передвижения роботов не выявлено. Каждый тип мобильности является наиболее подходящим для передвижения в тех или иных условиях. Также можно отметить, что самым перспективным типом мобильности является шагающий тип. Но из-за больших энергозатрат, малой скорости передвижения и сложности управления он на данный момент уступает колесному и гусеничному типу.

15. Рабочие органы манипуляционных роботов. Основные понятия. Захватные устройства. Классификация захватных устройств.

Рабочий орган робота - это составная часть его манипулятора, предназначенная для непосредственного захватывания и удержания объектов, перемещаемых в пространстве, а также выполнения различных технологических, специальных и исследовательских операций. Рабочие органы являются важными элементами роботов, во многом определяющими их универсальность и технологические возможности. К ним относятся захватные устройства, технологические инструменты и специальные устройства

В зависимости от назначения робота, решаемого им класса задач и особенностей выполняемого технологического процесса манипуляторы снабжаются теми или иными рабочими органами. Рассмотрим захватное устройство и технологические инструменты промышленных роботов, как наиболее распространенную и универсальную группу рабочих органов.

 

6.1. Захватные устройства

 

Захватные устройства (ЗУ), называемые часто захватами, предназначены для захватывания объектов манипулирования, надежного их удержания в процессе изменения пространственного положения, а также обеспечения их установки с заданной точностью относительно базовых поверхностей.

Принцип действия захватных устройств и их конструктивное исполнение весьма разнообразны и обусловлены формой, видом, маркой материала, массой, размерами и физическими свойствами перемещаемых объектов, а также типом обслуживаемого технологического оборудования. Применяются как универсальные ЗУ, предназначенные для удержания различных по размерам, конфигурации и массе объектов, так и специальные, предназначенные для удержания определенного типа детали. Независимо от конкретного исполнения к захватным устройствам предъявляется ряд общих требований: они должны обеспечивать надежность захватывания и удержания объектов, быстродействие, стабильность базирования, обладать достаточными прочностью и жесткостью при минимальных размерах и массе, не должны допускать разрушения или повреждения поверхности объектов манипулирования. Особое внимание при проектировании следует > обращать на крепление ЗУ к "руке" робота, которое должно быть удобным, надежным, а при необходимости - легко- и быстросменным. Как правило, роботы, в особенности промышленные (ПР), снабжены набором сменных ЗУ, которые можно заменять в зависимости от конкретных технологических условий, а также устанавливать на типовые ЗУ сменные рабочие элементы (губки, присосы, подхваты и т.п.), при этом их смена в обоснованных случаях производится автоматически с помощью самого робота

16. Кинематические схемы захватных устройств. Расчет механических захватных устройств. Вакуумные и магнитные захватные устройства. Способы создания вакуума для захватных устройств манипуляционных роботов.

17. Коэффициент мехатронности и критерий совершенства мехатронной системы.

18. Проектирование следящих приводов роботов: краткая характеристика основных этапов.

19. Проектирование манипуляторов: основные этапы: краткая характеристика основных этапов.

20. Нейросетевое распознавание. Сеть Хопфилда. Сеть Хэмминга. Классификатор Гроссберга.

Среди различных конфигураций искуственных нейронных сетей (НС) встречаются такие, при классификации которых по принципу обучения, строго говоря, не подходят ни обучение с учителем, ни обучение без учителя. В таких сетях весовые коэффициенты синапсов рассчитываются только однажды перед началом функционирования сети на основе информации об обрабатываемых данных, и все обучение сети сводится именно к этому расчету. С одной стороны, предъявление априорной информации можно расценивать, как помощь учителя, но с другой – сеть фактически просто запоминает образцы до того, как на ее вход поступают реальные данные, и не может изменять свое поведение, поэтому говорить о звене обратной связи с "миром" (учителем) не приходится. Из сетей с подобной логикой работы наиболее известны сеть Хопфилда и сеть Хэмминга, которые обычно используются для организации ассоциативной памяти. Далее речь пойдет именно о них.

Структурная схема сети Хопфилда приведена на Рис. 6. Она состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон связан синапсами со всеми остальными нейронами, а также имеет один входной синапс, через который осуществляется ввод сигнала. Выходные сигналы, как обычно, образуются на аксонах.

Рис. 6. Структурная схема сети Хопфилда.

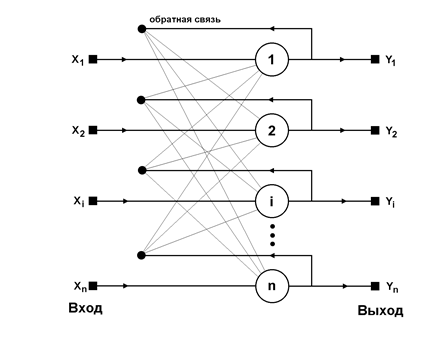
Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется следующим образом. Известен некоторый набор двоичных сигналов (изображений, звуковых оцифровок, прочих данных, описывающих некие объекты или характеристики процессов), которые считаются образцовыми. Сеть должна уметь из произвольного неидеального сигнала, поданного на ее вход, выделить ("вспомнить" по частичной информации) соответствующий образец (если такой есть) или "дать заключение" о том, что входные данные не соответствуют ни одному из образцов. В общем случае, любой сигнал может быть описан вектором X= { x_i: i=0...n-1}, n – число нейронов в сети и размерность входных и выходных векторов. Каждый элемент x_i равен либо +1, либо -1. Обозначим вектор, описывающий k-ый образец, через X^k, а его компоненты, соответственно, – x_i^k, k=0...m-1, m – число образцов. Когда сеть распознáет (или "вспомнит") какой-либо образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = X^k, где Y – вектор выходных значений сети: Y = { y_i: i=0,...n-1}. В противном случае, выходной вектор не совпадет ни с одним образцовым.

 

Если, например, сигналы представляют собой некие изображения, то, отобразив в графи­ческом виде данные с выхода сети, можно будет увидеть картинку, полностью совпадающую с одной из образцовых (в случае успеха) или же "вольную импровизацию" сети (в случае неудачи).

На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом:

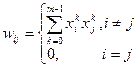 (1)

Здесь i и j – индексы, соответственно, предсинаптического и постсинаптического нейронов; x_i^k, x_j^k – i-ый и j-ый элементы вектора k-ого образца.

Алгоритм функционирования сети следующий (p – номер итерации):

1. На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непо­сред­ственной установкой значений аксонов:

y_i(0) = x_i , i = 0...n-1, (2)

поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от y_i означает нулевую итерацию в цикле работы сети.

2. Рассчитывается новое состояние нейронов

, j=0...n-1 (3)

и новые значения аксонов

 (4)

Рис. 7. Активационные функции.

где f – активационная функция в виде скачка, приве­денная на Рис. 7а.

3. Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.

Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов m не должно превышать величины, примерно равной 0.15•n. Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.

Рис. 8. Структурная схема сети Хэмминга.

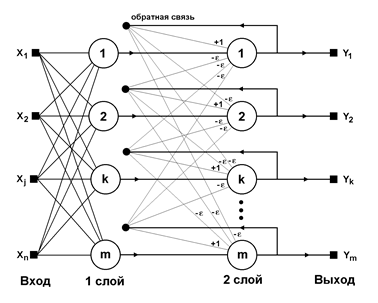
Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры (Рис. 8).

Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.

Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:

, i=0...n-1, k=0...m-1 (5)

T_k = n / 2, k = 0...m-1 (6)

Здесь x_i^k – i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 < e < 1/m. Синапс нейрона, связанный с его же аксоном имеет вес +1.

Алгоритм функционирования сети Хэмминга следующий:

1. На входы сети подается неизвестный вектор X = {x_i:i=0...n-1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

, j=0...m-1 (7)

После этого полученными значениями инициализируются значения аксонов второго слоя:

y_j⁽²⁾ = y_j⁽¹⁾, j = 0...m-1 (8)

2. Вычислить новые состояния нейронов второго слоя:

 (9)

и значения их аксонов:

 (10)

Активационная функция f имеет вид порога (рис. 2б), причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.

Из оценки алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).

21. Сети на основе радиально-базисных функций. Обучение без учителя в нейросетевом распознавании образов.

Сеть радиально-базисных функций — искусственная нейронная сеть, которая использует радиальные базисные функции как функции активации.

Выходом сети является линейная комбинация радиальных базисных функций входов и параметров нейрона. Сети радиальных базисных функций имеют множество применений, в том числе функции приближения, прогнозирования временных рядов, классификации и системыуправления.

Впервые сформулированы в 1988 Брумхедом и Лоу.

22. Самоорганизующаяся сеть Кохонена. Нейроэволюционное распознавания образов.

Самоорганизующиеся нейронные сети Кохонена (СНСК) обеспечивают топологическое упорядочивание входного пространства образов. Они позволяют топологически непрерывно отображать входное n-мерное пространство в выходное m-мерное, m<<n. Входной образ проецируется на некоторую позицию в сети, кодируемую как положение активированного узла. В отличие от большинства других методов классификации и кластеризации, топологическое упорядочивание классов сохраняет на выходе подобие во входных образах [2,10], что является особенно полезным при классификации данных, имеющих большое количество классов. Например, при классификации локальных участков изображений, может быть очень большое число классов, в которых переход от одного класса к другому практически непрерывен, затрудняя определение границ классов. Сети такого типа состоят из одного слоя (не считая входного), который так же может быть организован в n-мерную решётку, в зависимости от размерности выходного пространства. Каждый нейрон связан со всеми входными нейронами. Настройка весов сети осуществляется методом конкурентного обучения, в процессе которого изменяются только веса нейрона-победителя, имеющего максимальную активность. Существует так же метод, в котором изменяются и веса нейронов, соседних с победителем. В самоорганизующихся картах Кохонена (СКК), в отличие от векторных квантователей, нейроны решётки имеют связи с соседними нейронами, сила связей зависит от расстояния между ними. Для СНСК характерна высокая скорость обучения.

В [10] трёхмерная СКК (по 5 узлов на каждое измерение) применялась для уменьшения размерности локальных участков изображения 5х5 (размерность 25). Входное изображение отображается на один из 125 узлов, положение которого в трёхмерной решётке кодирует вектор выходного пространства. Три измерения СКК принимаются за три ключевых характеристики (features [10]). Такое преобразование обеспечило частичную устойчивость к изменению освещения, смещениям и искажениям, избавило от необходимости предварительной обработки изображения (преимущество – ускорение работы), а так же значительно ускорило процесс обучения и классификации, делая эту систему применимой в реальном времени (использовалась для распознавания лиц). Отмечено так же небольшое преимущество СКК перед методом анализа главных компонент, которое заключалось в более высокой точности последующей классификации на основе данных уменьшенной размерности.

Нейронная сеть с радиально-базисной функцией (НСРБФ) является дальнейшим развитием НС Кохонена, в которой после конкурентного слоя добавлен ещё один слой, обучаемый по методу обратного распространения. В отличие от НС Кохонена в НСРБФ выходами нейронов конкурентного слоя являются значения функции Гаусса с нормальным законом распределения, и обнуление не победивших нейронов не требуется. Ширина радиально-базисной функции характеризует расстояние между центром кластера, который образуется каждым нейронным элементом и его ближайшими соседями.

В [9] применялись две различные архитектуры НСРБФ для распознавания лиц. На вход сети поступали предварительно извлечённые характеристики, полученные методом анализа главных компонент или коэффициенты вэйвлетных преобразований. В первой архитектуре количество выходов соответствовало количеству классов, во второй применялся коллектив сетей, каждая из которых была обучена распознавать только свой класс. Отмечены значительные преимущества классификации НСРБФ перед непосредственным сравнением ключевых характеристик.

В [15] применялись две различные архитектуры ансамблей НСРБФ для предварительной классификации изображений. На вход сети поступало изображение целиком, на выходах формировалась промежуточная классификация, которая затем подавалась на решающие деревья для контекстно-ориентированного распознавания изображений лиц (например: “найти все изображения определённого человека, где он в очках”). Различные сети в ансамблях первой архитектуры учились классифицировать изображения с различными типами изменений, второй – с одинаковыми, но количество нейронов менялось в процессе обучения. Решающий вывод делал “судья”, который принимал решение на основе голосования ансамбля сетей.

23. Приложения методов распознавания образов: машинное зрение, распознавание рукописных символов, распознавание речи. Алгоритм однослойного перцептрона. Многослойный перцептрон.

24. Конечно-автоматные графы. Определение, формализованная запись. Их использование для математического описания логических процессов.

Конечный автомат — абстрактный автомат, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные способы задания конечного автомата. Например, конечный автомат может быть задан в виде упорядоченной пятерки:  , где

•  — входной алфавит (конечное множество входных символов), из которого формируются входные цепочки, допускаемые конечным автоматом;

•  — множество состояний;

•  — начальное состояние  ;

•  — множество заключительных состояний  ;

•  — функция переходов, определенная как отображение  , такое, что  , то есть значение функции переходов на упорядоченной паре (состояние, входной символ или пустая цепочка) есть множество всех состояний, в которые из данного состояния возможен переход по данному входному символу или пустой цепочке (λ).

Конечный автомат начинает работу в состоянии q₀, считывая по одному символу входной цепочки. Считанный символ переводит автомат в новое состояние в соответствии с функцией переходов. Читая входную цепочку x и делая один такт за другим, автомат, после того как он прочитает последнюю букву цепочки, окажется в каком-то состоянии q'. Если это состояние является заключительным, то говорят, что автомат допустил цепочку x.

Конечные автоматы широко используются на практике, например, в синтаксических и лексических анализаторах, тестировании программного обеспечения на основе моделей.