6 Закон движения центра масс

Скорость центра масс равна первой производной радиус-вектора центра масс по времени: .

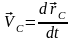Массу тела можно рассматривать как сумму элементарных масс системы:

.

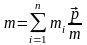Радиус-вектор центра масс определяется выражением: .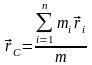

Тогда скорость центра масс будет равна: .

Следовательно, 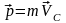– импульс системы равен произведению массы механической системы на скорость центра масс.

Если полученное значение импульса системы подставить во II закон Ньютона для механической системы в дифференциальной форме, то получим:

,

–

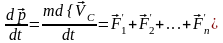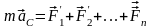закон движения центра масс: центр масс системы материальных точек движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.

Вывод: для замкнутых систем действие внешних сил равно нулю или скомпенсировано: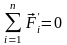 , т.е. .

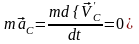Следовательно, 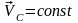– т.е. центр масс замкнутых систем движется равномерно.

Центр масс замкнутой системы относительно произвольной инерциальной системы отсчета движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил.

Внутренние силы не влияют на характер движения замкнутой системы тел, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе.

Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела – снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила – сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.

7 Уравнение движения тела переменной массы

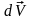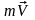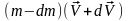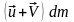Пусть в момент времени t масса ракеты m, а скорость . Через время dt масса ракеты изменилась на dm, а скорость ракеты на . Тогда: – начальный импульс ракеты; – конечный импульс; – импульс вытекающих газов.

Найдем изменение импульса ракеты за время dt:

.

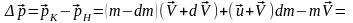
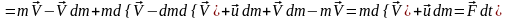Если полученное выражение разделить на dt, то получим:

.

Если 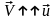, то ракета тормозится; если , то ракета движется с ускорением. Следовательно, – реактивная сила, которая создается вытекающими газами массы dm со скоростью .

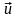Полученное уравнение: 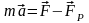носит название уравнения Мещерского

9 Формула Циолковского

Если система «ракета-газы» замкнута, то действие внешних сил отсутствует, т.е. . Тогда уравнение Мещерского преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

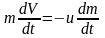при , .

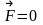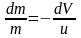После интегрирования получим: .

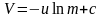В начальный момент времени, когда 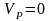, , 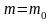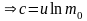. Тогда получаем:

–

формулу Циолковского, где определяется скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

Формула Циолковского показывает, что:

1. чем больше конечная масса ракеты, тем больше стартовая масса ракеты;

2. чем больше скорость истечения газа, тем больше может быть конечная масса ракеты.

РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ

ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ

План