2.1.4. Метод Ньютона

Алгоритм минимизации целевой функции (1.1) по методу Ньютона предусматривает итерационный процесс

, (2.7)

где Х^(j) — вектор неизвестных в j-ом приближении;

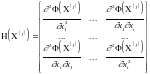, (2.8)

Матрица Гессе вторых частных производных, взятых в точке Х^(j), а градиент целевой функции имеет выражение

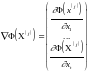. (2.9)

Применим алгоритм Ньютона к целевой функции метода наименьших квадратов

, (2.10)

где Р_i — веса измерений.

В этом частном случае для градиента целевой функции в сим­волах Гаусса получим

.

где А - матрица коэффициентов уравнений поправок;

Р - диагональная матрица весов измерений;

L. - вектор свободных членов уравнений поправок.

Зная первые частные производные целевой функции (2.10), получим вторые частные производные и в символах Гаусса приме­нительно к матрице (2.8) запишем

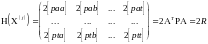
Окончательно вместо (2.7), сокращая двойки, в матричной форме получим

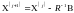, (2.11)

что соответствует алгоритму Гаусса.

Отметим, что метод Гаусса, определяемый матричным выраже­нием (2.11), есть частный случай метода Ньютона, описываемого выражением (2.7), поскольку последний применим не только для целевой функции (2.10), но и для других целевых функций. Поэто­му алгоритм (2.11) в математической литературе еще называют ме­тодом Ньютона-Гаусса. Объединяет эти два метода общий недоста­ток: в методе Ньютона используется линеаризация при вычислении численным способом первых и вторых частных производных крите­риальной функции, в методе Гаусса также используется линеариза­ция при вычислении элементов матрицы А.

Для численного определения по параметрам первых частных производных целевой функции, входящих в (2.9), используют фор­мулы (2.3) - (2.5).

Вторые смешанные частные производных можно вычислить по из­вестной формуле численного дифференцирования

,

где значения целевой функции определяются в точках, показанных на рис. 2.5.

Вторые квадратичные частные производные можно найти по формуле

,

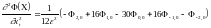где значения целевой функции вычисляются в точках, показанных на рис. 2.6.

x₁

Рис. 2.5. Расположение точек для численного определения

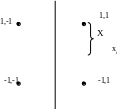
смешанных вторых частных производных

- 2,0 -1,0 0,0 1,0 2,0

Р ис. 2.6. Расположение точек для численного определения

квадратичных вторых частных производных.

Если геодезическая сеть содержит более десяти определяе­мых пунктов, значения Ф_i,j вычислять достаточно долго. Поэтому надо знать Ф_0,0 и находить любое Ф_i,j по фор­муле

,

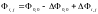где DФ_0,0 - приращение целевой функции для данной пары па­раметров без изменения координат пунктов; DФ_i,j - прираще­ние целевой функции с измененными на величину e координа­тами.

Специальные исследования, проводимые на персональной ЭВМ показали, что для численного вычисления вторых частных произ­водных следует брать e не по формуле (2.6), а из выражения

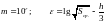, (2.12)

которое позволяет находить e для численного вычисления про­изводных при данной разрядной сетке ЭВМ с наивысшей точностью.