1.19. Енергія електричного поля

1.19.1. Перехідні процеси в конденсаторі

Функції заряджання і розряджання записуються:

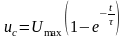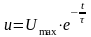, (1.64)

де u_c – поточне значення напруги, на обкладках конденсатора, В; U_max– максимальне значення напруги В; е – основа натурального логарифму безрозмірна величина, е=2,71 t – тривалість заряджання, с;  –стала заряджання, константа електричного кола, яке має з’єднуючі електропроводи із загальним електричним опором R і конденсатор, ємність якого, С.

. (1.65)

Розмірність сталої часу:

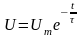
Рис. 1.5. Функція зростання і спадання напруги між обкладками конденсатора при його заряджанні і розряджанні:

По завершенні заряджання (орієнтовно трохи менше проміжку часу, що дорівнює 3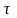 ) напруга на обкладках конденсатора буде

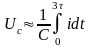. (1.66)

1.19.2. Енергія електричного поля зарядженого конденсатора

Зарядження конденсатора супроводжується роботою, яку виконує при цьому джерело електроенергії при заряджанні конденсатора.

. (1.67)

Наприкінці заряджання в електричному полі конденсатора буде накопичуватися енергія, миттєве значення якої

, (1.68)

де W – миттєве значення енергії електричного поля конденсатора, Дж; – заряд, що наповнює ємність конденсатора за час зарядження, Кл; t – час заряджання, с; 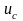– поточне значення напруги на обкладках конденсатора.

Тобто кінцеве значення енергії електричного поля конденсатора згідно (1.67) і (1.68) буде

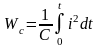або 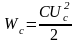. (1.69)

(1.69) визначає енергію зарядженого конденсатора.

1.19.3. Об’ємна щільність енергії електричного поля

Розглянемо плоский конденсатор, обкладки якого мають площу S, відстань між ними дорівнює х. Нехай середовище має відносну діелектричну проникність .

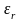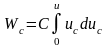, (1.70)

де С – ємність простору, Ф; u_с – миттєве значення напруги (різниця потенціалів) між крайніми границями простору довжиною х шириною S.

Аналогічно із (1.69) на підставі (1.70) запишемо:

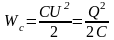, (1.71)

де Q – заряд, що є у згаданому вище пристрої (конденсаторі), об’єм якого

. (1.72)

Модуль вектора індукції

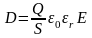. (1.73)

Враховуючи, що

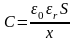та 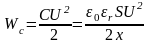(1.74)

запишемо, врахувавши (2.39):

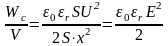. (1.75)

Отже об’ємна щільність енергії

w_e= (1.76)

Рівняння (1.76) визначає середню енергію, яка приходиться на одиницю об’єму простору, у якому є електричне поле. Розділ 2 магнітне поле

2.1. Загальні поняття про магнітне поле

Магнітне поле – це властивість простору, яка полягає в силовій його дії на змінні в цьому просторі і часі електричне поле, а також заряд або систему зарядів. Особливе значення для пізнання магнітного поля має зміна стану одного заряду стосовно другого. На рис 2.1 показано систему двох зарядів Q і q, які знаходяться на відстані R

Рис. 2.1 Система двох взаємодіючих зарядів

Q і q – взаємодіючі між собою заряди; R – відстань між зарядами,  – кутова швидкість обертання заряду q.

У взаємному спокої на заряд q електричне поле заряду Q діятиме із силою f.

= q (2.1)

де – сила кулона, Н; q – внесений в електричне поле заряд рухливий заряд, Кл; – напруженість електричного поля заряду Q в точці знаходження заряду q, В/м.

Якщо тіло із зарядом Q є нерухомим, а із зарядом q обертається навколо центра заряду Q із деякою лінійною швидкістю при незмінній відстані R між Q і q, то матимемо додаткову електричну силу fq, яку приписують дії на заряд q магнітного поля.

Отже розподіл сил електричної і магнітної, з якими взаємодіють заряди залежить від системи відліку, у якій ці сили взаємодіють. Розглянемо загальну силу, яка діє на заряд q, що обертається навколо заряду Q, яка носить назву сили Лоренца.