Добавил:

Kaz Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

Высшая математика

Файл:

Методические указания и контрольные работы по высшей математике ЖА Черняк, Минск 2004 (Мет пособие)

.pdf

Скачиваний:

Добавлен:

15.06.2014

Размер:

794.18 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

82. 1) lim x3 −3x + 2 ;

x→1 x2 − 4x +3

4) lim

tg2x −sin 2x

;

x→0

83. 1)

lim

3x2

+ 2x +1

;

x3 −8

x→2

4) lim

sin 7x + sin 3x

;

x→0

x sin x

84. 1)

lim

2x2

−3x −1

;

x4 −1

x→1

4) lim

cos 2x − cos 4x

;

x→0

arctg3x2

85. 1)

lim

2 + 7x − 4

;

x3 + 64

x→−4

2) lim x7 +5x2 − 4x ; x→∞ 3x2 +11x3 −7

5) lim x +1 5x ; x→∞ 2x −1

lim

1 +

4x − x

;

x→∞ x + 3x2 + 2x4

6x + 5

5) lim

;

x→+∞ x −10

lim

3x − x6

;

x→∞ x2 − 2x +5

2x −3 6x+1

;

5) lim

x→∞ x

+ 4

lim

7x2

+5x +9

;

4x − x3

x→−∞

	cos 4x −cos3 4x			x −1	3x
4) lim		; 5)	lim		;
4) lim	tg3x2	; 5)	lim	4x + 5	;
x→0	tg3x2		x→+∞	4x + 5

86. 1) lim

x3 + x −2

;

lim

3x4 + 2x2 −8

;

− x2 − x +1

8x3 − 4x +

x→1

x→−∞

cos2 x −cos2 2x

3x + 7 4x

4) lim

; 5)

lim

;

arcsin x2

x→0

x→−∞

x + 4

87. 1)

lim

4x3 − 2x2 + 5x

;

2) lim

−3x4 + x

;

3x2 + 7x

+3x −2

x→0

x→∞ x4

4) lim

arcsin 7x

;

x − 2

5x−1

lim

;

x→0 sin x +sin 7x

x→+∞

3x +10

88. 1)

lim

2 − x −30

;

lim

2x2 +10x −11

;

x3 +125

3x4 − 2x +5

x→−5

x→−∞

4) lim

arcsin 5x

;

4x +3 7 x

;

lim

2x2 − x

x→0

x→−∞

x +5

89. 1) lim

x2 + 2x − 24

;

lim

3x + 2 +14x2

;

2x3 +15x +

+ 2x + 7x2

x→−6

x→∞

3) lim	x +12 − 4 − x	;
x→−4	x2 + 2x −8

6) lim 2x − 4 −3x .

x→∞ 2x

3) lim

x2 + 4 − 2

;

x2 +16 − 4

x→0

1− x 3x

6) lim

x→∞ 2 − x

3) lim

;

1+ x −

x→0

1− x

2 −3x

6) lim

x→∞ 5 −3x

3) lim

x + 4 −3 ;

x→5

x −1 −2

4x −1

6) lim

4x +

x→∞

3) lim

2x +1 −3

;

x→4

x − 2 −

2x −1

−x

6) lim

x→∞ 2x +

3) lim

2x + 7 −5 ;

x→9

3 −

1 + 2x −x

6) lim

x→∞

3 + 2x

3) lim

2 −

;

x→4

6x +1 −5

3−2x

6) lim

x→∞ x −1

3) lim

x −3 −2 ;

x→7

x + 2 −3

1−cos8x

1 − x

15x+3

2x −4x

4) lim

;

lim

; 6) lim

x→0

3arctg 2 x

x→+∞

2 −10x

x→∞ 1

+ 2x

90. 1)

lim

3 − 2x − 4

;

2) lim

8x5 − 4x

3 +3

;

lim

4x +1 −3

;

−11x +18

2x3 + x

−7

3 −8

x→2

x→−∞

x→2

4) lim

sin 2 3x −sin 2 x

; 5)

x + 5

3x+7

− 2x x+1

lim

;

6) lim

tgx arctgx

x→0

x→−∞ 4x − 2

x→∞ 1

− 2x

Задачи 91-100. Исследовать функцию f(x) на непрерывность и построить ее график.

	− x,				x ≤ 0,
91. f(x)=						0 < x < 2,
	−(x −1)2 ,
		−3,			x ≥ 2.
	x
	− 2(x +1),					x ≤ −1,
93. f(x)=	(x +1)3 ,					−1 < x < 0,

				x ≥ 0.
	x,
		3	,		x < −1,
95. f(x)=	x
	x −1,				−1 ≤ x ≤ 3,
	5 − x,				x > 3.

	1,			x ≤ 0,
97. f(x)=					0 < x ≤ 2,
	2x ,
		+3,			x > 2.
	x
	−1+ x, x < 0,
99. f(x)=					0 ≤ x <π,
	sin x,
				x	≥π.
	3,

1− x, x ≤ 0,
	0		< x ≤ 2,
92. f(x)= 0,
			x > 2.
x − 2,
0,		x < −1,
			−1 ≤ x ≤1,
94. f(x)= 1− x,
			x >1.
ln x,
sin x,			x < 0,
		0	≤ x ≤ 2,
96. f(x)= x,
		x	> 2.
0,
	2	,	x ≤ 0,
− x
98. f(x)= tgx,			0 < x ≤π / 4,
		x >π / 4.
2,
x,			x ≤1,
100. f(x)= (x − 2)2 ,				1 < x < 3,

				x ≥ 3.
− x + 6,

Контрольная работа №3

Дифференциальное исчисление функций одной и нескольких переменных

		Задачи 101-110. Вычислить: 1-3) производную dy ; 4) производные						dy	и
	d 2 y						dx	dx
	d 2 y	; 5)	d 3 y	(x0) в данной точке x0; 6) производную n-го порядка для данной
	dx2	; 5)	d 3 y
	dx2		dx3
функции y(x).					2
	101. 1) y= 3 4x2 −3x − 4 −				2	;	2) y= arccos 2x 3−x ;
	101. 1) y= 3 4x2 −3x − 4 −				(x −3)5	;	2) y= arccos 2x 3−x ;
					(x −3)5

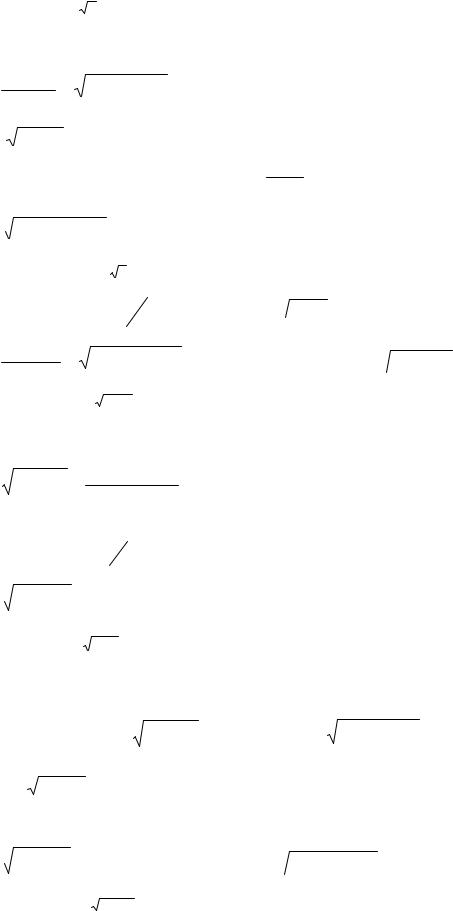
3) y=(cos5x)arctg

x ;

5) y= ln(2 + x2 ) , x0=0;

102.

y =

8x −3 + x2 ;

−1)3

y = ( 3x + 2)arccos3x ;

y = e−x cos x,

x0=0;

103.

y = 5 3x2 + 4x −5

;

− 4)6

y = (ln(2x −10))sin

x ;

y = x sin 2x ,

x0 =

−π

;

104.

y =

−7

5x −7x2 −3;

+ 2)4

y = (ctg(7x + 4)) 3x−5 ;

y = x4 ln x, x0 =1;

105.

y = 4 (x −1)5

−

;

7x2 −3x +

y = (log2 (5x + 7))ctg 2x ;

y = cos2 x ,

x0=π 4 ;

4)y-4x= e y ;

6)y= 2x .

2)y = arctg 4 5x ln(x2 + x −1);

4)3x +sin y = 5y ;

6)y = x 1+5 .

2)y = 5−x2 arcsin 3x3 ;

4)xy = ctg y ;

6)y = x +7 .

2)y = log3 (2x +5) arctg6x;

4)tg y = 3x + 6y ;

6)y = cos3x .

2)y = e−cos x arctg2x3 ;

4)y2 + x2 = sin y;

6)y =10x.

	6	3				3		6
106. 1)	y = 5 (x − 2) −		; 2)	y = ctg			4x arcsin5x		;
106. 1)	y = 5 (x − 2) −	(12x3 − x2 −4)4	; 2)	y = ctg			4x arcsin5x		;
3)	y = (lg(8x +3))	tg 2x ;	4) 4 sin2 (x + y)= x;
5)	y = x + arctgx ,	x0=1;	6)	y =	x		.
5)	y = x + arctgx ,	x0=1;	6)	y =	x +5		.
					x +5


	3					5
107. 1)	y =						− (x +1)	;
		(4x −3x2 +1)2
3)	y = (tg 2x + 3)log5 (3x+8);
5)	y = x4 ln x ,					x0=1;
108. 1)	y = 3 (x −8)		4	−		2			;
					(1+3x −4x2 )10
3)	y = (arcsin 6x)tg					10x+3 ;
5)	y = ln(x2 −4),					x0=3;

2)y = 2sin x 3 arccos2 3x;

4)y = 7x −ctgy;

6)y = ln(5x −1).

2)y = log3 (5x +1) arctg 3 4x;

4)xy −6 = cos y ;

6)y = e−3x .

109. 1)

y =

(3x2

− x +1)

;

y = 3

arcctg 5 2x lg(6x +1);

(3x

−7)5

y = (cos(4x +5))arcsin3x ;

4) x2 y2 + x = 5y;

y = sin(x3 +π),

x0 = 3 π ;

y = ln(3x −5).

110. 1)

y = 7 (2x +1)5 +

; 2)

y = log5 (7x − 2) arcsin2 x3 ;

(2x2 −4x +3)6

y = (tg7x3 )

x+2 ;

4) 3y-7=xy3;

y = x cos 2x,

x0 =π

;

y =

x +3

Задачи 111-120. Применяя формулу Тейлора с остаточным членом в форме Лагранжа, вычислить значение функции с точностью до 0,001.

111.	3	65 .	112. (3,03)5 .	113. cos151°.	114. e0,2 .	115. sin 29°.
116.	7	130 .	117. ln(e2 +0,2) . 118. (4,01)1,5 .		119. sin 93°.	120. e2,01 .

Задачи 121-130. Провести полное исследование данной функции и построить ее график.

121.	y = e2 x−x2 .					122.	y =	2(x +1)2			.	123.	y = xln2 x.
121.	y = e2 x−x2 .					122.	y =				.	123.	y = xln2 x.
								x − 2						x2
124.	y = xe 1x .					125. y = xex .						126.	y =	x2			.
124.	y = xe 1x .					125. y = xex .						126.	y =	(x + 2)2			.
														(x + 2)2
127.	y =	ln x		.		128.	y =	x4		.		129. y = ln(x			2	− 2x + 6).
127.	y =		x	.		128.	y =	x3 −		.		129. y = ln(x				− 2x + 6).
			x					x3 −	1
		1
130.	y = e		2−x		.

Задачи 131-140 .

131.Полотняный шатер объемом V имеет форму прямого конуса. Каково должно быть отношение высоты конуса к радиусу его основания, чтобы на шатер пошло наименьшее количество полотна?

132.Проволокой, длина которой l м, необходимо огородить клумбу, имеющую форму кругового сектора. Каким должен быть радиус круга, чтобы площадь клумбы была наибольшей?

133.Требуется сделать коническую воронку с образующей, равной 20 см. Какой должна быть высота воронки, чтобы ее объем был наибольшим?

134.Бревно длиной 20 м имеет форму усеченного конуса, диаметры оснований которого равны 2 м и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна, а объем был бы наибольшим. Каковы должны быть размеры балки?

135.Лампа висит над центром круглого стола радиусом r .На какой высоте надо разместить лампу над столом, чтобы освещенность предмета, лежащего на

краю стола, была наилучшей? (Освещенность прямо пропорциональна косинусу угла падения лучей и обратно пропорциональна квадрату расстояния от источника света.)

136.Канал, ширина которого a м, под прямым углом впадает в другой канал шириной b м. Определить наибольшую длину бревен, которые можно сплавлять по этой системе каналов.

137.Требуется изготовить открытый цилиндрический бак вместимостью V. Стоимость одного квадратного метра материала, из которого изготавливается дно бака, составляет а рублей, а стоимость одного квадратного метра материала, идущего на стенки бака, – b рублей. При каком отношении радиуса дна к высоте бака затраты на материалы будут минимальными?

138.Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен 15 см. При каком радиусе полукруга окно будет пропускать наибольшее количество света?

139.На странице книги печатный текст занимает площадь S. Ширина верхнего и нижнего полей равна а, а правого и левого полей – b. При каком отношении ширины к высоте текста площадь всей страницы будет наименьшей?

140.Из круглого бревна диаметром d требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб? (Сопротивление балки на изгиб Q пропорционально произведению ширины x ее попе-

речного сечения и квадрата ее высоты у, т.е. Q = kxy2 , k = const ).

Задачи 141-150. Вычислить приближенное значение функции с помощью дифференциала.

141.	3 0,953 + 0,174 0,792 .	142.		ln(0,922 − 0,183 0,84).
143.	arctg(0,792 + 0,113 0,923 ).	144.	1			.

	sin(0,153 − 0,21 0,782 ).			0,983 + 0,123 0,812
145.		146.	1			.
				0,973 0,122	0,872
147.	arcsin(0,173 − 0,21 0,97).	148.	arccos(0,123 − 0,11 0,923 ).

149. sin 2 (0,124 + 0,27 0,892 ).

150. cos2 (0,092 − 0,12 0,872 ).

Задачи 151-160. Написать:

1)уравнение касательной плоскости и нормали в точке (x0 , y0 , f(x,y)) к поверхности S, заданной уравнением z=f(x,y);

2)grad z в точке M0 (x0 ,y0);

3)производную функции z=f(x,y) в точке M0 (x0 ,y0 ) по направлению вектора ar.

151.	z = x2 + xy + y 2 ,			M 0 (1;1),	ar = 2ir − rj.
152.	z = ln(x2 + 3y 2 ),			M 0 (1;1),	ar = ir + rj.
153.	z = arctg(xy 2 ),			M 0 (2; −1),	ar = 5ir + 4 rj.
		x2			r	r	r
154.	z = arcsin		, M 0 (1; 2),		a	= 2i +	j.

		y

155.

z = e x2 +y2 ,

M 0 (1; 0),

ar = ir − 2 rj.

156.

z = 2x2 + 3xy + y 2 ,

M 0 (2;1),

ar = ir + 3rj.

157.

z = ln(5x2 + 4y 2 ),

M 0 (1;1),

ar = 4ir − 3rj.

(1;2), ar

158.

z = arccos

= i +

2 j.

159.

z = 2 x y ,

M 0 (2; −1),

ar = −3ir − 3rj.

160.

z = 3x4 + 2x2 y3 ,

M 0 (−1; 2),

ar = 3ir − rj.

Задачи

161-170.Найти наименьшее и наибольшее значения функции

z=f(x,y) в указанной области. Сделать чертеж области.

161. z = x

2 y(2 − x − y) в треугольнике, ограниченном прямыми x=0, y=0,

x+y=6.

162. z = x + y в круге

x2 + y2 ≤1.

163.

z = x3 + y3 −3xy

впрямоугольнике 0 ≤ x ≤ 2,

-1 ≤ y ≤ 2 .

164.

z = x2

−2y2 + 4xy −6x −1 в треугольнике, ограниченном прямыми x=0,

y=0, x+y=3.

165.

z = x

+ y2 − xy

в квадрате

≤1.

166.

z = x

− y2 в круге x2 + y2

≤1.

167.

z = x

+3y2 − x +18y −4

в треугольнике 0 ≤ x ≤ y ≤ 4 .

168 z = x −2 y −3 в области

0 ≤ x ≤1,

0 ≤ y ≤1,

0 ≤ x + y ≤1.

169.

z = x

+3y2 − x +18y −4 в квадрате 0 ≤ x ≤1,

0 ≤ y ≤1.

170.

z = x

+ y2 −12x +16y

в круге x2 + y2 ≤ 25 .

Задачи 171-180. Экспериментально получены пять значений функции y=f(x) при пяти значениях аргумента, которые записаны в табл. 1.

					Таблица 1
x	1	2	3	4		5
y	y1	y2	y3	y4		y5

Методом наименьших квадратов найти функцию вида Y=ax+b, приближенно выражающую (аппроксимирующую) функцию y=f(x). Сделать чертеж, на котором в прямоугольной декартовой системе координат построить экспериментальные точки и график аппроксимирующей функции Y=ax+b.

						Таблица 2
Задача	x	1	2	3	4		5
171	Y	5,2	3,7	3,1	1,8		1,2
172	Y	2,0	2,6	3,9	4,5		6,0
173	Y	5,4	3,9	3,3	2,0		1,4
174	Y	1,8	2,4	3,7	4,3		5,8
175	Y	5,6	4,1	3,5	2,2		1,6
176	Y	1,6	2,2	3,5	4,1		5,6
177	Y	5,8	4,3	3,7	2,4		1,8
178	Y	1,4	2,0	3,3	4,9		5,4
179	Y	6,0	4,5	3,9	2,6		2,0
180	Y	1,2	1,8	3,1	3,7		5,2

Контрольная работа №4

Неопределенный и определенный интегралы

Задачи 181-190. Найти неопределенные интегралы. В пп. 1-2 результат проверить дифференцированием.

181.

∫

5 2 x − 7 x

dx;

2)∫x2 cos 2xdx;

3)∫

x5 + 3x3 +1

dx.

x2 + x

182.

∫

2 cos 2x

dx;

2)∫x5 ln xdx;

3)∫

4x4 + 2x3 − x − 3

cos2 x sin 2

2x (x2 −1)

183. 1) ∫e x cos(1 + e x ) dx; 2)∫(x + 3) e−2x dx; 3)∫	-2x5 −8x3 + 3	dx.

	x2 − 2x

184. 1) ∫ (2 +3 xx )3 dx;

185.	1) ∫			sin 2x			dx;
			1 + cos2
					x
186. 1) ∫		3 arccos2			x	dx;
				1 − x2

187.	1) ∫			dx		;
		(1		+ x2 )
					arctgx

2)∫4x2arcctg x dx;

2)∫(sin 2x −1)x2dx;

2)∫sinx2 xdx;

2)∫5x cos2 x dx;

188.

1) ∫

x2dx

;

2)∫

x arccos x

dx;

e2x3+5

− x2

189.

1) ∫

; 2)∫sin(ln x)dx;

− x2 earcsin x

190.

1) ∫

sin 3 x dx

;

2)∫ln

2 − x

dx;

cos x

+ x

3)∫ x3 − 5x2 + 5x + 23 . (x2 −1)(x − 5)

3)∫ 2x4 − 5x2 − 8x −8dx. 3x(x2 − 4)

3)∫3x4 + 3x5 − 5x2 + 2 . 2 (x2 − x)(x + 2)

3)∫ 2x4 + 2x3 − 41x2 + 20dx. 3x(x2 + x − 20)

3)∫3x3 − x2 −12x − 2dx. 4x(x2 − x − 2)

3)∫ − x5 + 25x3 +13dx.

x2 + 5x

3)∫ 2x3 − x2 − 7x +12dx.

x3 − 2x2 −3x

Задачи 191-200. Вычислить определенные интегралы.

−π4 cos 3 x

dx;

2x − 8

dx.

191. 1)

∫

sin x

∫

−π

−1 2

1 − x −

π2

;

x 2

dx.

192. 1) ∫

2)∫

2 + cos x

8x − x 2

− 15

(

x +1 +

dx.

193. 1) ∫

sin x sin 2x sin 3x dx; 2)∫

x +1 −

;

194. 1) ∫

sin x

2) ∫

3 x +1

−1

π2

195.1) ∫ cos5 xdx;

196. ∫ cos2 x sin 4 xdx;

π2
π		dx
197. 1) ∫2		dx	;
π	3	sin3	x
	3

π3

198. 1) ∫ tg 4 xdx;

π4

199. 1) ∫3 sin3 x dx;

0 cos4 x

200.1) ∫4 1 + tgx dx;

π6 sin 2x

2		dx
2)∫		dx			.
2)∫					.
0 x +1 + (x +1)3
4
2) ∫3		dx		.
3	4	x x2 +1
	4
12		x2dx		.
2) ∫		1 − x2		.
	0	1 − x2
3
2) ∫4		dx		.
14		x(1 − x)
14
1		x3dx	.
2)∫		2 − x2	.
0		2 − x2
	3	x2 +	1	dx.
2) ∫		x2		dx.
	1	x2

Задачи 201-210. Вычислить приближенное значение определенного интеграла по методу: 1)прямоугольников; 2) Симпсона, разбивая промежуток интегрирования на 10 частей. Все вычисления производить с точностью до трех десятичных знаков после запятой.

201.	9	x3 + 2 dx.	202.	11	x3 + 3 dx.	203.	12	x3 + 4 dx.
201.	∫	x3 + 2 dx.	202.	∫	x3 + 3 dx.	203.	∫	x3 + 4 dx.
	−1			1			2
	8			10			12
204.	∫	x3 + 8 dx.	205.	∫	x3 + 5 dx.	206.	∫	x3 + 9 dx.
	−2			0			2
	8			8			7
207.	∫	x3 +11 dx.	208.	∫	x3 +16 dx .	209.	∫	x3 + 32 dx.
	−2			−2			−3
210.	5	x2 + 36 dx.
210.	∫	x2 + 36 dx.
	−5

Задачи 211-220.

211.Вычислить площадь фигуры, ограниченной линиями y = 2x , y = 2x − x2 , x = 0, x = 2.

212.Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y = 2x − x2 , y = 0 , вокруг оси Ox.

213.Вычислить длину дуги кривой y = ln x, x [ 3; 8].

214.Вычислить площадь фигуры, ограниченной линиями

y = x2 +1, x + y = 3.

215.Фигура, ограниченная кривой y = xex , прямыми y=0, x=1, вращается вокруг оси Ox. Найти объем тела вращения.

216.Вычислить длину дуги кривой y = ln cos x, x [0, π 4].

217.Вычислить площадь фигуры, ограниченной линиями

y = cos x, y = x +1, y = 0.

218. Вычислить объем тела, отсекаемого от параболоида x =

костью x=2.

219. Вычислить длину дуги кривой y = x 2 , 0 ≤ x ≤ 5.

220. Вычислить объем тела, отсекаемого от гиперболоида x2

плоскостями z=–2 и z=3.

y 2	+	z 2	плос-
2		4

+	y 2	−	z 2	=1
	9		16

Контрольная работа №5

Несобственные интегралы. Кратные интегралы

Задачи 221-230. Вычислить несобственный интеграл или установить его расходимость.

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
15.06.2014505.44 Кб24Высшая математика, 2ой семестр (Романчук) [2121 вопросов].docx
#
15.06.2014629.45 Кб21Контрольная работа 1,2 по ВМ для зачников вариант 4.pdf
#
15.06.2014529.92 Кб15КР 1 вар 4.doc
#
15.06.2014348.67 Кб12КР 2 вар 4.doc
#
15.06.2014259.58 Кб23Математический анализ (Мет пособие).doc
#
15.06.2014794.18 Кб56Методические указания и контрольные работы по высшей математике ЖА Черняк, Минск 2004 (Мет пособие).pdf
#
15.06.2014175.1 Кб54Примеры решения дифференциальных уравнений.doc
#
15.06.2014148.48 Кб66Примеры решения задач на интегралы.doc
#
15.06.2014767.49 Кб71Примеры решения задач с кратными интегралами.doc
#
15.06.2014422.91 Кб21Примеры решения на темы пределы,.doc
#
15.06.2014620.91 Кб33Руководство к выполнению контрольных работ по высшей математике ЖА Черняк, ТС Степанова, БГУИР 2002.pdf