
Автоматизация деятельности банков (Мет пособие)
.pdf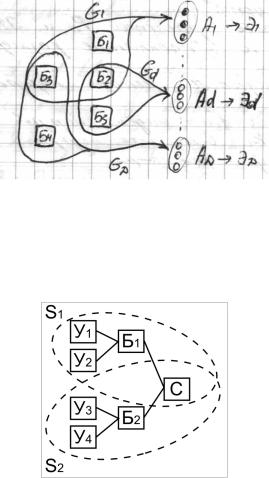
Э1+…+Эd+…+ЭД=Э Gd<<G
Пример:
Рассматривается система: У – устройство приемное.
Б – блок обработки.
С – суммирующее устройство.
Требуется определить математическое ожидание объема информации принятого, обработанного на интервале [0,t] и вероятность безотказной работы каждого элемента на этом интервале 0,9.
n
Э= ∑Эi Hi i=1
Свяжем состояние системы с вероятностью ее функционирования. У1-У2 – 40% получаемой информации.
У3-У4 – 60% получаемой информации.
Каждый блок или работает или не работает. Общее число состояний 27=128.
Можем уменьшить число состояний. За 40% ответственны блоки У1,У2,Б1,С – это 1ая группа. За 60% ответственны блоки У3,У4,Б2,С – это 2ая группа.
Х = работает; !Х – не работает.
S11(У1,!У2,Б1,С) – 1ый работает, далее комбинации. S11(У1,!У2,!Б1,С)
S11(У1,!У2,!Б1,!С)
S11(У1,!У2,Б1,!С)
S112(У1,У2,!Б1,С) – 1 ый и второй работают, остальные комбинации
S112(У1,У2,!Б1,!С)
S112(У1,У2,Б1,!С)
S112(У1,У2,Б1,С)
S12(!У1,У2,Б1,С)
S12(!У1,У2,!Б1,С)
S12(!У1,У2,!Б1,!С)
S12(!У1,У2,Б1,!С)
S10(!У1,!У2,Б1,С) – 1 ый и второй не работает. S10(!У1,!У2,!Б1,С)
S10(!У1,!У2,!Б1,!С)
S10(!У1,!У2,Б1,!С)
Красным помечены состояния, у которых эффективность 0. Их мы убираем.
H11=P1(1-P2)PБ1Pc=0,073
H12=P2(1-P1)PБ1Pc=0,073 H112=P1P2PБ1Pc=0,657
Блоки У1 У2 одинаковой мощности, обеспечивают равные доли эффекта.
Э11=0,2 I
51
Э12=0,2 I
Э112=0,4 I I – information
S23(У3,!У4,Б2,С)
S24(!У3,У4,Б2,С)
S224(У3,У4,Б2,С)
H23=0,073
H24=0,073
H224=0,657
Э23=0,3 I
Э24=0,3 I
Э224=0,6 I
2 |
∑ |
Эdν Hdν = 0,2I 0,073 + 0,4I 0,657 + 0,2I 0,073 + |
Э = ∑ |
+ 0,3I 0,073 + 0,6I 0,657 + 0,3I 0,073 = 0,365I |
|
d =1ν =1,12,2(при_ d =1) |
||
|
ν =3,34,4(при_ d =2) |
|
При разбиении G на d групп при двоичных состояниях (работает/не работает) число состояний уменьшается в
d2 раз.
ПРИМЕР ОЦЕНКИ ПОКАЗАТЕЛЯ ЭФФЕКТИВНОСТИ ВТОРОЙ ГРУППЫ ДЛЯ СИСТЕМ ДЛИТЕЛЬНОГО ДЕЙСТВИЯ
Рассматриваются варианты информационной подсистемы АСУБД (автоматические системы управления безопасности движения). Варианты систем отличаются месторасположением и числом радиолокационных станций. Рассмотрим 2 варианта:
Зона ответственности (прямоугольник), зона обнаружения и наблюдения за воздушным объектом с заданным качеством (окружность):
Рис???
Внутри круга обнаружение Р0>=P0порог, среднеквадратичное отклонение: σx,y,h<=σпорог
Красная пунктирная линия – траектория полета. Точки – точки в которых определяется положение системы. Эти точки спроецированы на прямую времени. Качество информации, которую мы получаем оценивается в каждой точке (k1..k7). Свяжем состояния системы с обнаружением воздушного объекта.
Система 1:
Н0 – ни один не видит объект.
Н1 – первый видит, второй не видит. Н2 – второй видит, первый не видит. Н12 – оба видят.
Система 2:
Н0 – ни один не видит объект.
Н1 – первый видит, остальные не видят. Н2 – второй видит, остальные не видят. Н3 – третий видит, остальные не видят. Н12 – 1,2 видят, остальные не видят.
Н13 – 1,3 видят, остальные не видят. Н23 – 2,3 видят, остальные не видят.
H |
0 |
(1− P (1)) |
|
|
H 1 |
= P (3) (1− P (3)) |
||
|
1 |
1 |
|
|
3 |
1 |
2 |
|
H |
1 |
= P (1) |
|
|
H 2 |
= P (3) (1− P (3)) |
||
|
1 |
1 |
|
|
3 |
2 |
1 |
|
H |
0 |
= (1− P (3))(1− P (3)) |
|
H 12 |
= P (3) P (3) |
|||
|
3 |
1 |
2 |
|
3 |
2 |
1 |
|
H |
3 |
= P (3)(1− P (3))(1− P (3)) |
|
|
|
|||
|
3 |
3 |
1 |
2 |
|
|
|
|
КЛАССИФИКАЦИЯ ПРАКТИЧЕСКИХ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ СЛОЖНЫХ СИСТЕМ |
||||||||
|
|
|
|
|
|
|
||
N |
|
|
Оценка эффективности |
|
|
|
||
показателя |
|
|
|
|
|
|
|
|
1 |
|
|
Путем сравнения данной системы с оптимальной и оптимально функционирующей. Суть – вводится |
|||||
|
|
|
понятие «идеальной системы» и с ней сравниваются другие. |
|||||
2 |
|
|
Экстремум |
функционала, называемого |
показателем |
цели управления. Цель управления, например, |
||
52

|
|
обеспечить на данный момент на такой-то момент времени. |
|
3 |
|
Выполнение системой функциональных обязанностей: |
|
|
|
Надежность. |
|
|
|
Степень простоты обслуживания. |
|
|
|
Величина ущерба при отказе. |
|
|
|
Наличие резервов. |
|
4 |
|
Вероятность выполнения системой своих задач. |
|
5 |
|
Функция ошибок. Он развернут во времени, т.е. отслеживается динамика изменения ошибок. |
|
6 |
|
Вероятность выполнения задачи на требуемом уровне за определенное время. |
|
7 |
|
Вероятность того, что система будет удовлетворять заданным техническим условиям, в заданных |
|
|
|
условиях эксплуатации в течение требуемого периода времени. |
|
8 |
|
Степень приближения конструкции к эталонной конструкции, апробированной на практике. |
|
9 |
|
Максимум вероятности того, что система удовлетворяет всем заданным техническим требованиям. |
|
10 |
|
Эффективность системы определяется показателем практической оптимальности. |
|
11 |
|
Эффективность определяется по одному из частных показателей: быстродействие, СКО ошибки, |
|
|
|
надежность. |
|
12 |
|
Эффективность оценивается векторным показателем. В качестве такого показателя рассматривается |
|
|
|
совокупность показателей качества. |
|
|
Эти показатели можно свести в следующие группы: |
||
|
|
|
|
Номера |
|
|
Оценка эффективности |
показателей |
|
||
1,8 |
|
|
По эффективности системы эталона |
2,5 |
|
|
По экстремуму целевой функции |
4,6 |
|
|
По вероятности выполнения задачи без учета экономических факторов. |
3 |
|
|
По вероятности выполнения задачи с учетом экономических факторов. |
7,9 |
|
|
По максимуму вероятности того, что система удовлетворяет всем заданным техническим |
|
|
|
требованиям. |
11 |
|
|
По частным показателям. |
10,12 |
|
|
По совокупности конструктивных, эксплуатационных и экономических факторов. |
Показатели 2, 3, 10 – не имеют физического смысла, но позволяют сравнивать системы по эффективности. Показатели 3,4,6,7,9,10 – рассчитываются по статистическим данным.
Показатели 3,5-7,10,12 – оперируют вероятностью выполнения задачи. Наиболее правильный подход.
Показатель практической оптимальности системы (10)
n
∑bi yi
γ = i=1
c
b – весовые коэффициенты. y – частные показатели.
с – стоимость.
АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМ, ОПЕРАЦИЙ, ПРОЦЕССОВ
КЛАССИФИКАЦИЯ ЗАДАЧ И МЕТОДОВ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
1.План снабжения предприятий. Есть поставщики, есть потребители, необходимо так обеспечить сырьем, чтобы минимизировать, например транспортные расходы.
2.Планирование, внедрение сырья в производство.
3.Продажа сезонных товаров. Организуется ярмарка – определить количество товаров для получения максимальной прибыли.
4.Военные операции.
Общее в задачах:
Все задачи развернуты во времени.
Есть условия зависящие от нас и не зависящие.
Необходимо принять оптимальное решение. Решение включает параметры операции. Динамика процесса – это и есть операция.
Цель исследования операций – предварительное количественное обоснование оптимального решения.
53
Вводим вектор X=(x1,…,xi,… xn) – вектор решений. Множество управляемых условий проведения операций: {α }.
Множество неуправляемых условий проведения операций: {β } .
Для количественного исследования операций вводится показатель эффективности – Е, и строится математическая модель операции:
E / = (x X ,{α },{β })
/= - оператор модельного отображения. Он показывает, с помощью какой математики мы строим модель, т.е. указывает на аппарат.
Написанное выше выражение читается так: найти такое х, принадлежащее Х, которое обеспечило экстремум Е с учетом совокупности α и β .
Применяемые разделы математики применяемые: Математическое программирование. Теория массового обслуживания.
Теория игр. Теория графов.
Методы Монте-Карло (статистических испытаний). Теория расписаний.
Комбинаторика. Теория автоматов.
ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассматривается класс задач, для которого математическая модель операций имеет вид:
E / = (x X ,{α },{β }) → extr ,
т.е. β известна и вся поглощена α . Необходимо найти такой х, принадлежащий Х, которые бы обеспечили
экстремум Е с учетом ограничений на Х. Ограничения на Х отражаются совокупностью α . Задачи с такой постановкой - задачи математического программирования.
Математическое программирование – метод, указывающий вычислительную процедуру, которая приводит к решению задачи, т.е. программу решения задачи. Виды задач МП:
Линейное программирование. Развито. Нелинейное программирование. Динамическое программирование. Стохастичное программирование. Квадратичное программирование. Многоцелевое программирование.
Наиболее изучены задачи линейного программирования. Вид такой задачи:
E = c1 x1 + c2 x2 + ...+ cn xn → extr
Ограничения накладываемые на целевую функцию:
a11x1 + a12 x2 + ...+ a1n xn ≤ (≥ )b1
am1 x1 + am2 x2 + ...+ amn xn ≤ (≥ )bm
x1…xn – компоненты решения.
сi и аj – коэффициенты.
m – число уравнений ограничений.
Все задачи линейного программирования приводят к общему виду (основная задача линейного программирования):
E = c1x1 + c2 x2 + ... + cn xn → max (**)
a11x1 + a12 x2 + ... + a1n xn = b1 |
|
am1x1 + am2 x2 + ... + amn xn = bm |
(*) |
Все неравенства заменены равенствами.
Допустимые решения ОЗЛП: набор неотрицательных (x1…xn) которые бы удовлетворяли системе (*). Оптимальное решение (x*1…x*n) – то из допустимых, которое приводит к экстремуму функций (**).
ТРАНСПОРТНАЯ ЗАДАЧА
Есть пункты отправления: {Aj} Есть пункты назначения: {Bi}
Известна стоимость перевозки единицы топлива, запасы и потребность. Необходимо найти план перевозок, который бы минимизировал затраты на перевозку.
{Aj} |
{Bi} |
Запасы топлива |
54

|
B1 |
B2 |
B3 |
|
А1 |
С11=4 |
С12=9 |
С13=3 |
а1=20 |
А2 |
С21=4 |
С22=8 |
С23=1 |
а2=30 |
Потребность |
b1=10 |
b2=30 |
b3=10 |
|
Общая стоимость перевозки: С=С11Х11+ С12Х12+ С13Х13+С21Х21+ С22Х22+ С23Х23 Больше, чем есть в пункте мы не вывезем:
Все больше 0:
x11 + x12x21 + x22
x11 + x21x12 + x22x13 + x23
x > 0
ij
+x13 ≤ a1
+x23 ≤ a2
=b1
=b2
=b3
ПРИВЕДЕНИЕ ЗАДАЧИ ЛП К ОЗЛП
Максимизировать целевую функцию Е=4X1-X2+2X3 при ограничениях: 3X1+2X2-X3>=4
X1-2X2+3X3<=10 X1,X2,X3>=0
3X1+2X2-X3-4>=0 X1-2X2+3X3-10<=0
3X1+2X2-X3-4>=0 -X1+2X2-3X3+10<=0
3X1+2X2-X3-4=Y1 -X1+2X2-3X3+10=Y2
X1,X2,X3,Y1,Y2>=0
СУЩЕСТВОВАНИЕ РЕШЕНИЯ ОЗЛП И СПОСОБЫ ЕГО НАХОЖДЕНИЯ
Есть ограничения: |
|
A11X1+…+A1nXn=B1 (1) |
|
… |
|
Am1X1+…+AmnXn=Bm |
|
И целевая функция: C1X1+…+CnXn -> max |
(2) |
1.m=n – тогда привлекается аппарат обычной алгебры. Одно единственное решение.
2.m>n – поступаем, как и в случае 1, но до этого делаем так, чтобы m=n.
3.m<n – тогда система 1 имеет бесчисленное множество решений. Нас из этого множества интересуют только те наборы, которые положительны. Здесь варианты:
Система (1) несовместна. Решений нет.
Система совместна, но захватывает область отрицательных значений – решений нет.
ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ОБЛАСТИ ДОПУСТИМЫХ РЕШЕНИЙ
Рассмотрим случай n>m на 2:
Определяют m базисных переменных. (n-m) – свободные переменные.
Уравнение (1) разрешают относительно базисных переменных.
55

X3, Xm – базисные переменные.
X1,X2 – свободные переменные.
X3=a31X1+a32X2+B3 (3)
…
Xn=an1X1+an2X2+Bn
X1,X2 – координата точки.
Получим уравнение прямой: X3=0: a31X1+a32X2+B3=0
Рис???
Нас интересуют решения правее этой прямой.
Для прямой x4 нас не устраивают решения ниже прямой, далее для x5…
Часть полуплоскости, удовлетворяющая всем ограничениям, и будет областью допустимых решений. Подставив 3 в целевую функцию 2, получим запись целевой функции через X1,X2.
С=A31X1+A32X2+B3
C=U1X1+U2X2+U0
Если С принадлежит минимизации передвигаем параллельным переносом прямую назад и ищем минимальное значение.
Выводы:
Для оптимального решения, как минимум 2 переменные = 0. Оптимальное решение находится на одной из вершин многоугольника. Решения для вершин называются опорными решениями.
Оптимальное решение – это то из опорных, которое приводит к экстремуму целевую функцию С. Оптимальное решение отыскивается переходом от одной опорной точки к другой.
Симплекс-метод оптимизирует процедуру перебора опорных решений, т.е. следующее опорное решение не хуже предыдущего.
Эффективность симплекс-метода зависит от того, насколько быстро он приводит нас к оптимальному решению.
Рассмотрим случай, когда система не совместна.
ОДР не ограничена.
Бесчисленное множество решений.
56

ОПРДЕЛЕНИЕ БАЗИСНЫХ ПЕРЕМЕННЫХ
Определить базисные переменные для E=3x1+2x2 -> max. Ограничения:
X1+3X2<=270 4X1+6X2<=600 3X1+X2<=240 X1,X2>=0
-X1-3X2+270>=0 -4X1-6X2+600>=0 -3X1-X2+240>=0
-X1-3X2+270=X3 -4X2-6X2+600=X4 -3X1-X2+240=X5 X1,X2,X3,X4,X5>=0
E=3X1+2X2 -> MAX X1+3X2+X3=270 4X1+6X2+X4=600 3X1+X2+X5=240 X1,X2,X3,X4,X5>=0
В качестве базисных переменных берем те переменные, которые входят в каждое из уравнений с коэффициентом 1 и исключена из остальных уравнений. В целевую функцию они входят с нулевыми коэффициентами. Берем: x3,x4,x5.
РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ ГРАФИЧЕСКИМ МЕТОДОМ
См. условие выше.
x11 + x12 |
+ x13 ≤ |
20 |
||
x21 + x22 + x23 ≤ |
30 |
|||
x11 + x21 |
= 10 |
|
||
x |
+ x |
22 |
= 30 |
|
12 |
+ x |
= 10 |
|
|
x |
23 |
|
||
13 |
|
|
|
|
Свободные переменные: x11,x12.
x13=20-x11-x12 x21=10-x11 x22=30-x12
x23=30-(10-x11)-(30-x12)=-10+x11+x12 C=330-2x11-x12 -> min x11,x12,x13,x21,x22,x23>0
Рис???
Решение:
{Aj} |
{Bi} |
|
|
Запасы топлива |
|
B1 |
B2 |
B3 |
|
А1 |
x11=10 |
x12=10 |
x13=0 |
а1=20 |
А2 |
x21=0 |
x22=20 |
x23=10 |
а2=30 |
Потребность |
b1=10 |
b2=30 |
b3=10 |
|
57
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ
В ряде случаев есть ограничения по целочисленности компонент входящих в задачу. Т.е. нас интересуют дискретные точки ОДР (ОДР превращается в набор дискретных точек). Оптимальное решение находится в одной из дискретных точек. Например, если бы мы в транспортной задаче везли бы станки.
С=c1x1+…+cnxn -> max
a11x1+…+a1nxn=b1 (1)
…
am1x1+…+amnxn=bm xi>=0, i принадлежит n1
xj>=0,целые, j принадлежит n2 n1 и n2=n
Это частично целочисленная задача. А если n2=n, то полностью.
Решаем задачу симплекс-методом. Если полученное решение целочисленно, то все в порядке. В ином случае применяем метод Гомори. Метод Гомори:
1.Вводится дополнительное ограничение (уравнение) в систему ограничений.
2.Это дополнительное ограничение проходит через дискреты ОДР и отсекает оптимальное решение.
3.Задача с расширением ограничений снова решается симплекс-методом. Если полученное решение дискретно, то все завершается, если нет, то вводится дополнительное ограничение.
Требование целочисленности ухудшает целевую функцию.
Пример: 21x1+11x2 -> max 7x1+4x2<=13 x1,x2>=0
x1,x2 – целые.
Решение симплекс-методом: x1=13/7; x2=0.
Попробуем просто округлить: x1=2, x2=0 – не попало в ОДР. x1=0, x2=1
x1=0, x2=2 x1=0, x2=0 x1=1, x2=0 x1=2, x2=1
x1=0, x2=3 – вот оптимальное решение.
Отказ от целочисленности называется ослаблением исходной задачи целочисленной задачи линейного программирования. Ослабление решается путем введения дополнительных ограничений на переменные.
Пример: 5x1+x2 -> max (1) 2x1+x3=3 (2) x1,x2>=0 (3) x1,x2 – целые (4)
Если решим без учета целочисленности: x1=3/2, x2=0; Введем дополнительное ограничение:
X1<=1 (5)
И решим с ограничениями 1,2,3,5. Решение x1=1, x2=1.
ВЫБОР КТС (КОМПЛЕКСНО-ТЕХНИЧЕСКИХ СРЕДСТВ) НА РАННИХ СТАДИЯХ ПРОЕКТИРОВАНИЯ
В КТС входят: технические средства, программные средства. Задача: необходимо выбрать КТС по 2м основным параметрам: Производительность процессора.
Емкость памяти.
Y1 – производительность процессора.
Y2 – емкость памяти.
Они не определены – будем их рассматривать, как случайные величины. К1 и К2 – требуемые значения, соответственно процессора и памяти.
58
α 1 |
≤ |
K1 |
|
≤ α 2 |
|
|
|||||
|
|
|
Y1 |
||
β 1 |
≤ |
|
K2 |
≤ β 2 |
|
|
|
||||
|
|
|
Y2 |
||
α1, β1 - заданный уровень дефицита. α2, β2 - заданный уровень избытка.
α=0,7 α=1,4 β=0,9 β=1,5
СтоимостьКТС<=5.
Разработчик обладает следующей статистикой по Y: Табл 1.
Y1 |
0,2*106 |
|
0,4*106 |
0,6*106 |
0,8*106 |
1*106 |
|
1,4*106 |
1,6*106 |
||||||
P(Y1) |
0,05 |
|
|
0,1 |
|
0,3 |
0,3 |
|
0,1 |
|
0,1 |
0,05 |
|||
|
Табл 2. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Y2 |
0,3 |
|
0,5 |
0,7 |
0,9 |
|
1,5 |
2,5 |
|
|
||
|
|
|
P(Y2) |
0,06 |
0,05 |
0,1 |
0,4 |
|
0,3 |
0,1 |
|
|
|||
Разработчик располагает 5 альтернативами КТС: Таблица 3.
Si |
S1 |
S2 |
S3 |
S4 |
S5 |
k1i |
0,3 |
0,6 |
0,9 |
1,5 |
2,5 |
k2i |
0,5 |
1,0 |
1,5 |
2,0 |
3,0 |
k3i |
0,7 |
1,2 |
2,2 |
3,5 |
4,6 |
k3i – стоимость.
Выбрать из этих 5 вариантов комплекс, который бы удовлетворял заказчика. В качестве критерия выбора разработчик предлагает степень удовлетворения требований:
???
При этом разработчик имеет положительный опыт использования математического программирования. Решаем задачу в условиях риска (параметры У1 и У2 имеют распределение).
Критерий эффективности выбора:
???
Задача свелась к целочисленной модели программирования. Переход к матожиданию:
???
Вводим ограничения на компоненты, входящие в целевую функцию: Выбираем только 1 вычислительный комплекс из той 5ки, которую имеем: ???
???
Теперь запишем задачу в числовом виде. М1 рассчитываем с помощью Табл 1:
???
М2 рассчитываем с помощью Табл 2:
???
Преобразуем таблицу 3:
Si |
S1 |
S2 |
S3 |
S4 |
S5 |
k1i*М1 |
0,48 |
0,96 |
1,45 |
2,4 |
3,75 |
k2i*М2 |
0,55 |
1,1 |
1,65 |
2,2 |
3,3 |
E=1,03X1+2,06X2+3,1X3+4,6X4+7,05X5->max
???
Решим эту задачу, но предварительно сузим пример: ограничимся первыми тремя вычислительными комплексами:
Параметры |
|
ВК |
|
|
1 |
2 |
3 |
k1i |
0,3 |
0,6 |
0,9 |
k2i |
0,5 |
1 |
1,5 |
k3i |
0,7 |
1,2 |
2,2 |
Возьмем только следующие ограничения (для упрощения решения):
???
59
|
Распределение |
Варианты Y1,Y2 |
||||
|
|
1 |
2 |
|
3 |
|
|
Y2 |
0,2 |
0,4 |
|
0,6 |
|
|
P(Y1) |
0,3 |
0,4 |
|
0,3 |
|
|
Y2 |
0,3 |
0,5 |
|
0,7 |
|
Получили: |
P(Y2) |
0,2 |
0,5 |
|
0,3 |
|
|
|
|
|
|
|
|
M1=3, M2=2,1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Si |
S1 |
S2 |
|
S3 |
|
|
k1i*М1 |
0,9 |
1,8 |
|
2,7 |
|
|
k2i*М2 |
1,05 |
2,1 |
|
3,15 |
|
|
k1i*М1+ k2i*М2 |
1,95 |
3,9 |
|
5,85 |
|
Запишем формальную постановку задачи:
???
При ограничениях:
???
Приведем эту задачу к ОЗЛП: 0,9x1+1,8x2+2,7x3+x4=1,5 1,05x1+2,1x2+3,15x3-x5=0,9 0,7x1+1,2x2+2,2x3+x6=2
x1+x2+x3=1 xi=0;1 i=1,2,3. X4,x5,x6>=0
Уйдем от x3 заменой: X3=1-x1-x2.
Получаем:
F(X)=5,85 -3,9x1-1,95x2->max 1,8x1+0,9x2-x4=1,2 2,1x1+1,05x2+x5=2,25
???
Алгоритм:
1.Решается задача до получения оптимального плана.
2.Если оптимальное решение целочисленное, то процесс заканчивается, если нет, то переходим к следующему пункту.
3.На основании последней симплекс-таблицы оптимального плана для базисной переменной, имеющей наибольшую дробную часть, строится сечение. Сечение – это дополнительное ограничение.
4.Добавление сечения к условиям оптимального нецелочисленного плана приводит к расширенной задаче, после чего возврат к пункту 1.
1.Определим начальный опорный план. Для этого исходную задачу разрешим относительно базисных переменных:
х3 – х6. X3=1-x1-x2
X4=-1,2+1,8x1+0,9x2
X5=2,25-2,1x1-1,05x2 X6=-0,2+1,5x1+x2 Xi=0;1, i=1,2,3 X4,x5,x6>=0
???F(X)=5,85-3,9x1-1,95x2
2. Заносим задачу в симплекс-таблицу
Базисные переменные |
Свободные члены |
Свободные переменные |
||
|
|
-x1 |
-x2 |
i |
Х3 |
1 |
1 |
1 |
1 |
Х4 |
-1,2 |
-1,8 |
-0,9 |
2 |
Х5 |
2,25 |
2,1 |
1,05 |
3 |
Х6 |
-0,2 |
-1,5 |
-1 |
4 |
F |
5,85 |
3,9 |
1,95 |
5 |
j |
0 |
1 |
2 |
|
Т.к. среди СЧ есть отрицательные – план не является опорным. Алгоритм нахождения начального опорного
плана:
60
