Методические указания к выполнению контрольной работы № 1 Методические указания к заданию № 1

В регионе уровень дохода среднестатистической семьи равен 21 тысяче рублей. Минимальные затраты на товары первой необходимости равны 6 тыс. рублей, а на товары второй необходимости – 9 тыс. рублей. Целевая функция потребления товаров первой, второй необходимости и предметов роскоши определяется функцией , где – минимальные затраты на товары первой необходимости, – минимальные затраты на товары второй необходимости, – затраты на предметы роскоши. Затраты определяются в тысячах рублей.

Определить оптимальные затраты на потребления товаров, при которых суммарная полезность потребляемых товаров будет максимальной, а также максимальную оценку полезности. Предполагается, что доход не используется на накопление.

Решение. Используя решение задачи об оптимальном выборе в случае необходимых затрат на продукты разных видов, определим дополнительные затраты на товары каждого вида . Они равны разности общих и минимальных затрат на данный вид товара: . Затраты на дополнительное потребление равны: . Вычислим их. =21 – 6 – 9 = 6 тыс. рублей.

Дополнительные затраты на виды продуктов распределяются пропорционально степеням α₁, α₂, α₃. Поэтому , , . По условию α₁=1/4, α₂=1/2, α₃=9/8, тогда α=α₁+α₂+α₃=1/4+1/2+9/8=15/8.

Вычислим дополнительные затраты для каждого вида товаров: = = =0,8 тыс. рублей; = = =1,6 тыс. рублей; = = =3,6 тыс. рублей.

Тогда суммарная полезность набора товаров равна: = =10,11.

Вычислим полные затраты по каждому виду продуктов: = 6+0,8 = 6,8;

= 9+1,6= 10,6; = 3,6.

Ответ: 6,8 тыс. руб.; 10,6 тыс. руб.; 3,6 тыс. руб.; 10,11.

Методические указания к заданию № 2

Выпуск продукции на предприятиях отрасли определяется производственной функцией тонн, где – количество сырья, потребляемое ежемесячно на предприятии отрасли, – количество трудовых ресурсов, задействованных в производстве на предприятии отрасли. Стоимость сырья 16 тыс. рублей за тонну, средняя зарплата 20 тыс. рублей. Найти минимальные производственные затраты и количества используемых ресурсов, если объём выпуска продукции равен 46,129 тонн.

Решение. Используем решение задачи о минимальных затратах.

Сначала найдём степень однородности производственной функции, коэффициент : . После этого вычислим минимальные затраты для заданного уровня производства по формуле: .

Таким образом, = = 2500 тыс. рублей.

Используя необходимое условие оптимального выпуска продукции, определим затраты по каждому ресурсу в отдельности и из условий: и .

Тогда = = 500 тыс. руб., = = 2000 тыс. руб.

В миллионах затраты выражаются: = 0,5 млн руб, = 2,5 млн руб, = 2,5 млн руб,

Вычислим оптимальные объёмы ресурсов, используемые в производстве:

= = = 31,5 тонн, = = = 100 человек.

Ответ: = 31,5 тонн; = = = 100 человек; = 2,5 млн. рублей.

Методические указания к выполнению контрольной работы № 2 Методические указания к заданию №1

Фермерское хозяйство, ориентированное на выращивание яровой пшеницы и овса, имеет 80 га пашни, 630 человеко-дней трудовых ресурсов и 1800 л топлива, которые используются в течение производственного цикла. Планируется реализовать выращенную продукцию из расчёта 3600 рублей с 1 га, засеянного пшеницей, и 2900 рублей с 1 га, засеянного овсом.

Технологические коэффициенты потребностей в трудовых ресурсах и в топливе на 1 га в течение всего цикла приведены в табл. 24.

Потребность в трудовых ресурсах и в топливе на 1 га Таблица № 24

	Яровая пшеница	Овёс
Трудовые ресурсы (чел. -дни)	9	7
Топливо (л)	20	24

1. Составить экономико-математическую модель задачи при условии максимизации выручки от реализации культур в конце цикла в виде задачи линейного программирования;

2. Решить поставленную задачу графическим способом;

3. Составить двойственную задачу;

4. Найти решение двойственной задачи по решению прямой задачи;

5. Определить оценку полезности используемых ресурсов и их дефицитность;

6. Определить для каждой культуры, выгодно ли её выращивать.

Решение. 1) Определим переменные задачи: пусть x₁ – площадь пашни, засеянная яровой пшеницей; x₂ – площадь пашни, засеянная овсом.

Составим ограничения на использование ресурсов: пашни, трудовых ресурсов и топлива.

а) Площадь пашни, засеянная культурами, составит x₁ + x₂ га. Ограничение на использование пашни: x₁+x₂ 80 .

б) Общее использование трудовых ресурсов за цикл равно 9x₁ + 7x₂ трудодней. Ограничение по использованию трудовых ресурсов за цикл: 9x₁ + 7x₂ 630 .

в) Суммарное потребление топлива за цикл равно 24x₁ + 20x₂ литров.

Ограничение на потребление топлива: 20x₁ + 24x₃ 1800 .

г) Суммарная выручка Z от реализации яровой пшеницы и овса составит:

Z = 3600x₁ + 2900x_2. Учитывая условие максимизации выручки, получим задачу линейного программирования:

2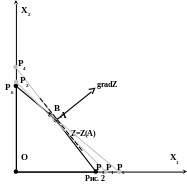 ) Решим задачу графически.

а) Найдём область допустимых решений как пересечение решений неравенств системы условий. Решения неравенств и ОДР представим на рис. 1.

Решаем первое неравенство:

x₁+x₂ ≤ 80. Граница решения этого неравенства описывается уравнением: x₁+x₂=80. Это уравнение прямой. Обозначим её l₁. Построим l₁ по двум точкам. Прямая l₁ проходит через точки: P₁(80;0) и P₂(0;80) (рис. 1). Определим

искомую область по контрольной точке. Возьмём точку О(0;0). Подставим её

координаты в первое неравенство:

0+0 < 80. Отношение верное. Решение первого неравенства содержит точку О (рис. 1).

Решим второе неравенство: 9x₁+7x₂ ≤ 630. Граница решения этого неравенства описывается уравнением: 9x₁+7x₂ = 630. Обозначим прямую, определяющуюся этим уравнением, через l₂. Построим её также по двум точкам: P₃(70;0) и P₄(0;90) (рис. 1). Определим искомую область по контрольной точке. Возьмём точку О(0;0). 9∙0+7∙0 ≤ 630. Решение второго неравенства содержит точку О.

Решим третье неравенство: 20x₁+24x₂ ≤ 1800. Граница решения этого неравенства тоже прямая, описывается уравнением: 20x₁+24x₂ = 1800.Обозначим её l₃. Она проходит через точки P₅(90;0) и P₆(0;75) (рис. 1). Определим искомую область по контрольной точке. Возьмём точку О(0;0). 20∙0+24∙0 <1800. Решение третьего неравенства содержит точку О.

Определяем ОДР: ОДР = OP₃АВР₆ (рис. 1).

б) Построим линию уровня и градиент. В качестве линии уровня целевой функции выберем прямую, проходящую через точку Р₃. Эта прямая – линия уровня Z = Z(P₃) =

= 3600∙70 +2900∙0 = 252000. Уравнение этой линии уровня: 3600x₁+2900x₂ = 252000. Координаты градиента целевой функции Z равны коэффициентам при соответсвующих переменных в этой целевой функции: grad Z = (3600;2900). Так как размеры градиента не входят в рисунок, рассмотрим вектор, сонаправленный с градиентом, например

n = 1/100 grad Z = (36;29) (рис. 1).

в) определим решение задачи, передвигая линию уровня в направлении градиента. Решением будет точка А – точка пересечения прямых l₁ и l₂. Найдём координаты точки А, решив систему уравнений .

, А(35;45). Х*=А=(35;45). Z(Х*) = 3600∙35 + 2900∙45 = 256500. Итак, решение задачи: Х*= (35;45), Z_max=256500.

3) Используя правила составления двойственной задачи, составим её. Учтём, что число переменных двойственной задачи равно трём, а число ограничений

двум.

u₁+9u₂+20u₃ ≥ 3600

u₁+7u₂+24u₃ ≥ 2900

u₁ ≥ 0, u₂ ≥ 0, u₃ ≥ 0

Z=80u₁+630u₂+1800u₃ → min.

4) Найдём решение двойственной задачи, используя вторую теорему двойственности. Для этого найдём остатки ресурсов при оптимальном плане Х*, которые обозначим переменными y_i*, i = 1, 2, 3.

y₁* = 80 – x₁*–x₂* = 80–35–45 = 0; y₂* = 630 – 9x₁*–7x₂* = 630–9∙35–7∙45 = 0;

y₃* = 1800 – 24 x₁*–20x₂* = 1800–20∙35–24∙45 = 20.

Проверим условия дополняющей нежёсткости:

x₁*v₁* = 0: x₁* = 35 ≠ 0 → v₁* = 0 → u₁* + 9u₂* + 20u₃* = 3600.

x₂*v₂* = 0: x₂* = 45 ≠ 0 → v₂* = 0 → u₁* + 7u₂* + 24u₃* = 2900.

y₁*u₁* = 0: y₁* = 0 → u₁* ≥ 0; y₂*u₂* = 0: y₂* = 0 → u₂* ≥ 0;

y₃*u₃* = 0: y₃* = 20 → u₃* = 0.

Тогда u₁*+ 9∙ u₂*+ 20∙0 = 3600 ; u₁*+ 7∙ u₂*+ 24∙0 = 2900

Получили систему уравнений для вычисления u₁* и u₂*.

,

Вычислим минимальное значение целевой функции двойственной задачи:

W(U*) = 80∙450 + 630∙350 + 1800∙0 = 256500 = Z_max . Оптимальные значения функций равны.

Решение двойственной задачи: U*=(450;350;0), V*=(0;0), W_min=256500 .

5) Так как y₃* = 20 ≠ 0, то топливо потребляется не полностью, является избыточным ресурсом. Оценки полезности пашни и трудовых ресурсов соответственно равны u₁*=450 ≠ 0 и u₂*=350 ≠ 0. Они отличны от нуля. Значит, пашня и трудовые ресурсы являются дефицитными ресурсами, их дополнительное использование эффективно.

6) Так как посевные площади x₁*=35≠ 0 и x₂*=45 ≠ 0, то яровую пшеницу и овёс выращивать выгодно.