
Проверка непараметрических гипотез
1) Ряд по цене однокомнатных квартир:
Рисунок 14 – интервальный ряд по цене однокомнатных квартир

Рисунок 15 – Показатели по ряду цен на квартиры
Выдвигается нулевая гипотеза:
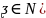 )
)
Альтернативная гипотеза:
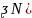 )
)
Для проверки нулевой гипотезы используют статистику:

k- число интервалов
 -
частоты
-
частоты
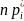 -
теоретические частоты
-
теоретические частоты
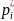 -
вероятность попадания нормально
распределенной случайной величины в
i-ый интервал
-
вероятность попадания нормально
распределенной случайной величины в
i-ый интервал
p( =
=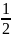 [Ф(
[Ф(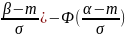 ]
]
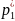 =p(
=p(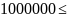 ᶚ
ᶚ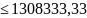 )=
)=
=
[Ф(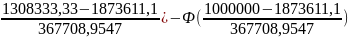 ]=
=
[-Ф(1,54)+Ф(2,38)]=
(-0,8764+0,9827)=0,05315
]=
=
[-Ф(1,54)+Ф(2,38)]=
(-0,8764+0,9827)=0,05315
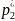 =p(
=p( ᶚ
ᶚ )=
)=
=
[Ф( ]=
=
[-Ф(0,6988)+Ф(1,5373)]=
(-0,5098+0,8764)=0,1833
]=
=
[-Ф(0,6988)+Ф(1,5373)]=
(-0,5098+0,8764)=0,1833
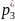 =p(
=p(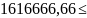 ᶚ
ᶚ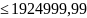 )=
)=
=
[Ф(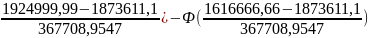 ]=
[Ф(0,139)+Ф(0,6988)]=
(0,1034+0,5098)=0,3066
]=
[Ф(0,139)+Ф(0,6988)]=
(0,1034+0,5098)=0,3066
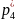 =p(
=p( ᶚ
ᶚ )=
[Ф(
)=
[Ф(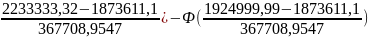 ]=
=
[Ф(0,9783)+Ф(0,139)]=
(0,6679-0,1034)=0,28225
]=
=
[Ф(0,9783)+Ф(0,139)]=
(0,6679-0,1034)=0,28225
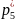 =p(
=p(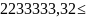 ᶚ
ᶚ )=
)=
=
[Ф(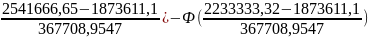 ]=
=
[Ф(1,82)-Ф(0,9783)]=
(0,9297-0,6679)=0,1309
]=
=
[Ф(1,82)-Ф(0,9783)]=
(0,9297-0,6679)=0,1309
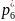 =p(
=p(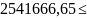 ᶚ
ᶚ )=
)=
=
[Ф( ]=
=
[Ф(2,66)-Ф(1,82)]=
(0,9922-0,9297)=0,03125
]=
=
[Ф(2,66)-Ф(1,82)]=
(0,9922-0,9297)=0,03125
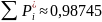
χ²расч=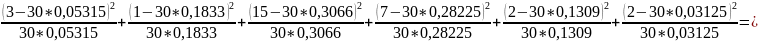 1,2389+3,68+3,6598+0,2543+0,9456+1,204=10,9826
1,2389+3,68+3,6598+0,2543+0,9456+1,204=10,9826
χ²кр(α=0,05;ν=3)=7,82
χ²расч˃ χ²кр=˃ Н0 отвергается.
Таким образом, можно сказать, что распределение отлично от нормального.
2) Ряд по количеству квадратных метров:
![]()
Рисунок 16 – Интервальный ряд по количеству квадратных метров

Рисунок 17 – Показатели по ряду по количеству квадратных метров
Выдвигается нулевая гипотеза: )
Альтернативная гипотеза: )
Для проверки нулевой гипотезы используют статистику:
k- число интервалов
- частоты
- теоретические частоты
- вероятность попадания нормально распределенной случайной величины в i-ый интервал
p( = [Ф( ]
=p(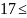 ᶚ
ᶚ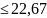 )=
)=
=
[Ф(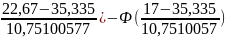 ]=
=
[-Ф(1,18)+Ф(1,705)]=
(-0,762+0,9109)=0,07445
]=
=
[-Ф(1,18)+Ф(1,705)]=
(-0,762+0,9109)=0,07445
=p(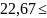 ᶚ
ᶚ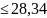 )=
)=
=
[Ф(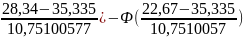 ]=
=
[-Ф(0,65)+Ф(1,18)]=
(-0,4843+0,762)=0,13885
]=
=
[-Ф(0,65)+Ф(1,18)]=
(-0,4843+0,762)=0,13885
=p( ᶚ
ᶚ )=
)=
=
[Ф(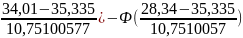 ]=
=
[-Ф(0,123)+Ф(0,65)]=
(-0,0955+0,4843)=0,1944
]=
=
[-Ф(0,123)+Ф(0,65)]=
(-0,0955+0,4843)=0,1944
=p(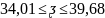 )=
)=
=
[Ф(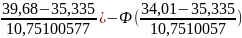 ]=
=
[Ф(0,404)+Ф(0,123)]=
(0,3108+0,0955)=0,20315
]=
=
[Ф(0,404)+Ф(0,123)]=
(0,3108+0,0955)=0,20315
=p(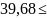 ᶚ
ᶚ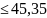 )=
)=
=
[Ф(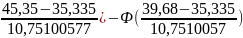 ]=
=
[Ф(0,93)-Ф(0,404)]=
(0,6476-0,3108)=0,1684
]=
=
[Ф(0,93)-Ф(0,404)]=
(0,6476-0,3108)=0,1684
=p(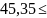 ᶚ
ᶚ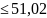 )=
)=
=
[Ф(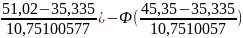 ]=
=
[Ф(1,45)-Ф(0,93)]=
(0,8529-0,6476)=0,10265
]=
=
[Ф(1,45)-Ф(0,93)]=
(0,8529-0,6476)=0,10265

χ²расч=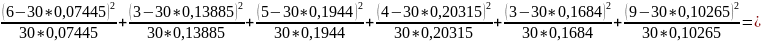 6,3517+0,3261+0,1187+0,7198+0,8335+11,3824=19,73226
6,3517+0,3261+0,1187+0,7198+0,8335+11,3824=19,73226
χ²кр(α=0,05;ν=3)=7,82
χ²расч˃ χ²кр=˃ Н0 отвергается.
Таким образом, можно сказать, что распределение отлично от нормального.
Однофакторный дисперсионный анализ.
Исследовать влияние наличия балкона на стоимость однокомнатных квартир.
Составим вспомогательную таблицу:

Рисунок 18 – Вспомогательная таблица
Выдвигается нулевая гипотеза: наличие балкона не влияет на стоимость однокомнатных квартир.
Альтернативная гипотеза: наличие балкона влияет на стоимость однокомнатных квартир.
Для проверки нулевой гипотезы строится статистика F:
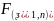 =
=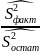
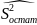 =
=
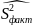 =
=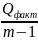
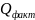 =
=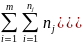
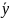 =1873611,1
=1873611,1
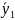 =1828751
=1828751
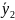 =1436583
=1436583
=18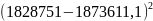 +12(
+12( =2328146436571,5
=2328146436571,5
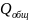 =4056296262037,04
=4056296262037,04
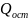 =
=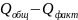 =4056296262037,04-2328146436571,5=1728149825465,54
=4056296262037,04-2328146436571,5=1728149825465,54
=
=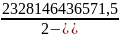 =2328146436571,5
=2328146436571,5
=
=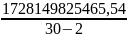 =61719636626
=61719636626
 =
=
=
=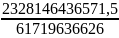 =37,72
=37,72
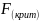 (α=0,05;
(α=0,05;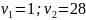 )=4,2
)=4,2
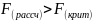 ,значит,
нулевая гипотеза отвергается, т.е.
наличие балкона влияет на стоимость
однокомнатных квартир.
,значит,
нулевая гипотеза отвергается, т.е.
наличие балкона влияет на стоимость
однокомнатных квартир.
Проверка гипотезы о равенстве двух средних выбранных уровней.
Выдвигается нулевая гипотеза:
:
Для проверки нулевой гипотезы строится статистика F:
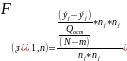
 =0,00004572
=0,00004572
(α=0,05; )=4,2
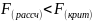 ,значит,нулевая
гипотеза принимается, т.е. средние равны.
,значит,нулевая
гипотеза принимается, т.е. средние равны.
