14. Механикалық жүйенің кинетикалық энергиясы және оның ішкі сыртқы күш жұмыстарымен байланысы.
Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема. Механикалық жүйеге ішкі және сыртқы күштер әсер етсін. Онда бұл жүйе үшін:
Бұл теңдеулерді өзара қосып және дифференциалдың белгісін қосындының белгісінің алдына шығарып, алатынымыз:
,
немесе
(15.9)
Бұл формула жүйенің кинетикалық энергиясының өзгеруі туралы теоремасының дифференциал түрін өрнектейді: механикалық жүйенің кинетикалық энергиясының дифференциалы жүйеге әсер ететін барлық сыртқы және ішкі күштердің элементар жұмыстарының қосындысына тең болады.
Соңғы
теңдеудің екі жағын да 
-ге
бөлейік. Онда
.
(15.10)
Сонымен, жүйенің кинетикалық энергиясының уақыт бойынша алынған бірінші туынды жүйеге әсер ететін барлық сыртқы және ішкі күштердің қуаттарының қосындысына тең болады.
Жүйе
өзінің 
алғашқы
орналасу жағдайынан 
ақырғы
орналасу жағдайына ауысып көшкенінде
интеграл алайық. Алған өрнектерді қосып,
алатынымыз
,
(15.11)
мұнда 
-
сәйкестеп алынған жүйенің алғашқы
орналасу және ағымды орналасу жағдайындағы
кинетикалық энергиясы; 
,
және 
k –
нүктесіне әсер ететін сыртқы және ішкі
күштерінің жұмысы.
Жүйенің кинетикалық энергияның өзгеруі туралы теореманың интегралдық түрдегі өрнегі былай айтылады: жүйенің бір орналасу жағдайынан екінші бір орналасу жағдайына көшу кезінде жасаған орын ауыстыруындағы кинетикалық энергиясының өзгеруі жүйеге әсер ететін барлық сыртқы және ішкі күштердің сол орын ауыстыруындағы жұмыстарының қосындысына тең болады.
15.1
мысал. Горизонталь
жазықтықта орналасқан эпициклдік
механизмнің ОА айналшағына
тұрақты айналдырушы L момент
әсер етеді (15.1,асурет).
Айналшақтың массасы m1, тісті
доңғалақтың массасы m2 .
Айналшақты жіңішке біртекті сырық деп,
ал радиусы 
тісті
доңғалақты біртекті табақша деп
айналшақтың бұрыштық жылдамдығының
айналу бұрышына тәуелділігін анықтау
керек. Қозғалмайтын тісті доңғалақтың
радиусы 
.
Бастапқы уақытында жүйенің күйі
тыныштықта болатын.
Шешуі. Қарастырып отырған механизм үшін Кинетикалық энергияның өзгеруі туралы теореманы интегралдық түрде жазайық:
(15.12)
(
,
яғни қозғалыс тыныштық күйден басталады).
Әр дененің кинетикалық энергиясы
болады,
мұнда 
.
15.1 - сурет
Қозғалмайтын және қозғалмалы тісті доңғалақтардың жанасу нүктесі қозғалмалы тісті доңғалақ үшін лездік жылдамдықтар центрі (ЛЖЦ) болып табылады. Сондықтан
.
(15.13)
Сонымен, айналшақтың айналып тұрғандағы механизмнің кинетикалық энергиясы
.
Әр дененің (айналшақ және қозғалмалы тісті доңғалақ) ішкі күштердің жұмысы нөлге тең болады. Айналшақ пен қозғалмалы тісті доңғалақтың өзара әсерлесу күштердің жұмысы да нөлге тең болады (бұл күштердің түсу нүктелерінің жылдамдықтары бірдей, ал Ньютонның үшінші заңы бойынша күштердің модульдері тең және бағыттары қарама-қарсы). Сондықтан
.
Механизм
горизонталь жазықтықта орналасқандықтан
оған әсер ететін ауырлық күштер жұмыс
жасамайды, яғни бұл күштер түсу нүктелердің
орын ауыстыруларына перпендикуляр
болады. Қозғалмалы және қозғалмайтын
тісті доңғалақтардың әсерлесуін 
және 
күштер
көрсетеді (15.1, б - сурет), олардың да
жұмысы нөлге тең болады, яғни бұл
күштердің түсу нүктесі
– ЛЖЦ. 
және 
реакциялары
қозғалмайтын нүктеге түсірілгендіктен,
олардың жұмыстары нөлге тең болады.
Сонымен, қарастырып отырған механизмге
түсірілген сыртқы күштерден жұмыс
жасайтын тек қозғалушы момент 
және
қозғалысқа кедергі жасайтын тұрақты
момент Мкед ,
яғни
,
мұнда 
- ОА айналшақтың
айналу бұрышы; 
-
қозғалмалы тісті доңғалақтың айналу
бұрышы.
(15.13)
кинематикалық қатынастан
табатынымыз: 
.
Онда
.
Тапқан қатынастарды (15.12) өрнекке апарып қойсақ, алатынымыз:
,
мұнда Jкел –
келтірілген инерция моменті, 
Lкел –
сыртқы күштердің келтірілген моменті, 
.
Сонымен, 
.
15.Сыртқы күш өрісіндегі материалдық нүтенің потенциалдық энергиясы және оның материалдық күшке әсер ететін күшпен байланысы.
Материалдық нүктелер жүйесі деп, олардың аяқталған санының жиынтығын айтамыз. Жуйенің әрбір нүктесіне екі түрлі сипаттағы күштер әсер етеді. Біріншіден, жүйеден тыс жерден әсер ететін сыртқы күштер, екіншіден, жүйе ішінде әчер ететін ішкі күштер.
Материалдық нүктелер жүйесіне әсер ететін барлық күштердің қосындысы былай анықталады:
,
(1.1)
мұндағы
жүйенің
iиндексімен
белгіленген материалдық нуктесіне әсер
ететін күш, ол
сыртқы
күш пен осы нүктеге әсер ететін
ішкі күштердің қосындысына тең.
Ньютонның үшінші заңы (3.1) өрнегін ықшамдауға кометеседі:
,
яғни, материалдық нүктелер жүйесіне әсер ететін күш тек сыртқы күштердің қосындысымен анықталады.
Күштерді қасиеттеріне қарай екі класқа бөлуге болады.
Жұмысы тек траекторияның бастапқы және соңғы нүктелеріне ғана байланысты, оның түріне байланыссыз күштерді потенциалдық (консервативті).күштер деп атайды.Оған тартылу күштері жатады.
Потенциалды өріс деп жұмысы тек траекторияның бастапқы және соңғы нүктелеріне ғана байланысты, оның түріне байланыссыз өрісті , жұмысы мына интегралға тең:
(5.6)
Енді мына бір математикалық теоремаға сәйкес: егер Fx , Fy , Fz потенциалдық күштің проекциялары болса, ондамынандай функция En(x, y, z) көмегімен осы проекциялар мына формулалармен беріледі:
(5.7)
функции Enфункциясы көмегімен күш жұмысын (5.5) өрнегінің оң жағынан табуға болады:
.
Интегралдап,1 нүктеден 2 нүктеге көшкен кездегі жұмысты анықтауға болады:
,
(5.8)
мұндағыEn1 жәнеEn2 – Enфункциясының 1 және 2нүктелердегі мәндері. (5.8) бен (5.5) ескере отырып аламыз:
.
(5.9)
Сонымен 1 және 2 арасындағы кинетикалық энергия Enшамасының кері мәніне өзгереді. Теңдікті мына түрде жазған ыңғайлы:
.
Осыдан кинетикалық энергия менEn–нің қосындысы қозғалыс кезінде тұрақты болып қалады:
.
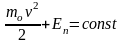(5.10)
Enшамасы материалдық нүктеніңпотенциалдық энергиясы , ал теңдік –я энергияның сақталу заңы.
Күшті вектор ретінде жазалық:
,
мұндағы
– координатостері
бойындағы бірлік векторлар.
Потенциалдық
күштердің проекциясын ескере отырып:
табамыз:
набла
операторын
қолдана отырып
,
мынаны аламыз
.
(5.11)