Задание 4.
Задана
система линейных уравнений в матричной
форме 
,
где A - известная матрица, Y - известный вектор, X - неизвестный вектор.
Требуется:
Задать матрицу A размером 10x10, вектор Y размером 1х10. Элементами матрицы A и вектора Y должны быть целые случайные числа от 0 до 10.
При задании матрицы использовать следующую формулу:
=ОКРВВЕРХ(СЛЧИС()*N;1), где N - номер варианта.
2. Используя специальную вставку, скопировать только значения матрицы A и вектора Y.
3. Найти определитель матрицы A.
4. Найти обратную матрицу B = A-1.
5. Проверить, что полученная матрица B является обратной.
6. Найти вектор X по формуле X = BY.
Решение.
Зададим матрицу A размером 10x10 и вектор Y размером 1х10. Элементами матрицы A и вектора Y будут целые случайные числа от 0 до 10, поскольку при задании матрицы была использована формула =ОКРВВЕРХ (СЛЧИС()*10;1), где N=10 - номер варианта.
Используя специальную вставку, скопируем только значения матрицы A и вектора Y.
Найдем определитель матрицы A.
Найдем обратную матрицу B = A-1
Проверим, что полученная матрица В является обратной.
Найдем вектор Х по формуле Х=ВY.
Задание 5.
Исходные данные распределения добавленной стоимости по отраслям экономики в ЕС в 2002 г. (выбрать любую из пар зависимого и независимого показателей).
1. Методом наименьших квадратов по табличным данным найти аппроксимирующие (приближаемые) функции, то есть регрессии: линейную, квадратичную, показательную, гиперболическую.
2. В каждом случае найти общую ошибку и среднюю ошибку аппроксимации. Указать функцию лучшей аппроксимации.
3. Построить линии регрессии на одной плоскости вместе с исходными данными.
Таблицу можно считать функцией, заданной таблично.
Решение.
Методом наименьших квадратов по табличным данным найдем аппроксимирующие (приближаемые) функции, то есть регрессии:
а) линейную, б) квадратичную, в) показательную, г) гиперболическую.
а) определим систему нормальных уравнений для нахождения оценок параметров линейной регрессии:
.
Для удобства расчетов представим таблицу исходных данных следующим образом:
№ |
Государство |
Промышленность, млрд. дол., х |
Сельское хозяйство, млрд. дол., y |
х2 |
х*у |
||||
1 |
Венгрия |
30,7 |
3,7 |
942,49 |
113,59 |
||||
2 |
Кипр |
20,3 |
4,1 |
412,09 |
83,23 |
||||
3 |
Латвия |
24,7 |
4,7 |
610,09 |
116,09 |
||||
4 |
Литва |
30,5 |
7,1 |
930,25 |
216,55 |
||||
5 |
Мальта |
28,1 |
2,8 |
789,61 |
78,68 |
||||
6 |
Польша |
30 |
3,1 |
900,00 |
93,00 |
||||
Сумма |
164,30 |
25,50 |
4 584,53 |
701,14 |
|||||
Получим систему нормальных уравнений для линейной регрессии:
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
В
блок «Переменные» в первую строку
записываем переменные системы
алгебраических уравнений
,
во вторую строку записываем произвольные
числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных .
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных »; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
Запишем уравнение полученной линейной регрессии:
.
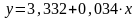б) определим систему нормальных уравнений для нахождения оценок параметров квадратичной регрессии:
-
параболы второй степени.
Составим вспомогательную таблицу и произведем расчеты, необходимые для составления системы нормальных уравнений.
№ |
Государство |
Промышленность, млрд. дол., х |
Сельское хозяйство, млрд. дол., y |
х2 |
х3 |
х4 |
х*у |
х2*у |
1 |
Венгрия |
30,7 |
3,7 |
942,49 |
28 934,44 |
888 287,40 |
113,59 |
3 487,21 |
2 |
Кипр |
20,3 |
4,1 |
412,09 |
8 365,43 |
169 818,17 |
83,23 |
1 689,57 |
3 |
Латвия |
24,7 |
4,7 |
610,09 |
15 069,22 |
372 209,81 |
116,09 |
2 867,42 |
4 |
Литва |
30,5 |
7,1 |
930,25 |
28 372,63 |
865 365,06 |
216,55 |
6 604,78 |
5 |
Мальта |
28,1 |
2,8 |
789,61 |
22 188,04 |
623 483,95 |
78,68 |
2 210,91 |
6 |
Польша |
30 |
3,1 |
900,00 |
27 000,00 |
810 000,00 |
93,00 |
2 790,00 |
Сумма |
164,30 |
25,50 |
4 584,53 |
129 929,76 |
3 729 164,39 |
701,14 |
19 649,89 |
|
На основании полученных результатов расчета коэффициентов система нормальных уравнений примет вид:
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
В
блок «Переменные» в первую строку
записываем переменные системы
алгебраических уравнений
,
во вторую строку записываем произвольные
числовые значения 0, 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных .
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных »; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
Запишем уравнение полученной квадратичной регрессии:
.
в) показательная регрессия сводится к нахождению уравнения вида:
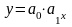
Логарифмирование
данного уравнения по основанию е
приводит к линейному уравнению вида:
.
Соответственно
оценки параметров
могут быть найдены методом наименьших
квадратов. Для упрощения и наглядности
решения произведем следующие замены
переменных:
.
Тогда уравнение в новых переменных будет иметь вид:
.
Определим систему нормальных уравнений для нахождения оценок параметров полученной линейной регрессии.
Составим таблицу для расчетов необходимых значений:
№ |
Государство |
Промышленность, млрд. дол., х |
Сельское хозяйство, млрд. дол., y |
Y |
x*Y |
х2 |
||||
1 |
Венгрия |
30,7 |
3,7 |
1,31 |
40,17 |
942,49 |
||||
2 |
Кипр |
20,3 |
4,1 |
1,41 |
28,64 |
412,09 |
||||
3 |
Латвия |
24,7 |
4,7 |
1,55 |
38,22 |
610,09 |
||||
4 |
Литва |
30,5 |
7,1 |
1,96 |
59,78 |
930,25 |
||||
5 |
Мальта |
28,1 |
2,8 |
1,03 |
28,93 |
789,61 |
||||
6 |
Польша |
30 |
3,1 |
1,13 |
33,94 |
900,00 |
||||
Сумма |
164,30 |
25,50 |
8,39 |
229,69 |
4 584,53 |
|||||
Получим систему нормальных уравнений для линейной регрессии:
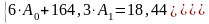
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
В
блок «Переменные» в первую строку
записываем переменные системы
алгебраических уравнений
,
во вторую строку записываем произвольные
числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных .
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных »; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
Уравнение регрессии в линейной форме будет иметь вид:
.
Выполнив его потенцирование, вернемся к показательной регрессии:
.
г)
гиперболическая регрессия сводится к
нахождению уравнения вида:
Для
оценки параметров заменим
,
тогда уравнение будет иметь вид:
.
Определим систему нормальных уравнений для нахождения оценок параметров полученной линейной регрессии.
Для расчетов используем данные таблицы:
№ |
Государство |
Промышленность, млрд. дол., х |
Сельское хозяйство, млрд. дол., y |
Х |
Х*y |
X2 |
1 |
Венгрия |
30,7 |
3,7 |
0,0326 |
0,12 |
0,001 |
2 |
Кипр |
20,3 |
4,1 |
0,0493 |
0,20 |
0,002 |
3 |
Латвия |
24,7 |
4,7 |
0,0405 |
0,19 |
0,002 |
4 |
Литва |
30,5 |
7,1 |
0,0328 |
0,23 |
0,001 |
5 |
Мальта |
28,1 |
2,8 |
0,0356 |
0,10 |
0,001 |
6 |
Польша |
30 |
3,1 |
0,0333 |
0,10 |
0,001 |
Сумма |
164,30 |
25,50 |
0,22 |
0,95 |
0,009 |
|
Получим систему нормальных уравнений для линейной регрессии:
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений , во вторую строку записываем произвольные числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных .
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных »; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
Уравнение регрессии в линейной форме будет иметь вид:
.
Вернемся к гиперболической регрессии:
.