§7. Ряд Фурье функции с произвольным периодом.

Пусть функция имеет период 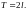Т.е.

y

Как и в случае 2π периодических функций не ограничивая общности, будем рассматривать её на .

2l

l

-l

x

Рассмотрим линейное отображение на .

B(l,π)

x

t

A(-l,-π)

L

l

-l

π

-π

Уравнение прямой 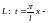искомое отображение,

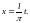
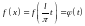
Легко видеть, что 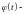периодическая, периода 2π, т.е.:

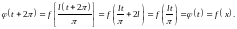
Разложим функцию 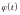в ряд Фурье:

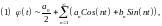где

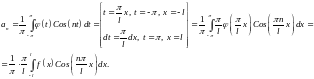
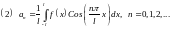
Аналогично:

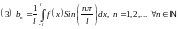
Подставляя в (1) 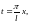получим:

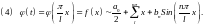
Простое объяснение перехода.

Замена 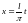переводит 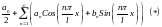ряд в ряд

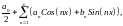
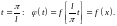
Формула (4) задаёт ряд Фурье функции , а (2) и (3) – коэффициенты Фурье этой функции.

Пример. Разложить в ряд Фурье на (-2, 2) функцию .

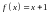2

-2

1

x

y

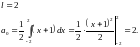
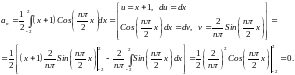
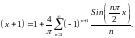
Df. Пусть 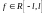. Тогда тригонометрический ряд

называется рядом Фурье для функции на , если его коэффициенты вычисляются по формулам Фурье (2) и (3).

Замечание. Если ряд (4) сходится на 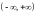к функции , то его сумма есть периодическая с периодом

Следствие. Пусть тригонометрический ряд (4) сходится равномерно на к функции . Тогда этот ряд является рядом Фурье для своей суммы .

Следует иметь ввиду, что замена переводит ряд (4) в ряд (1), имеющий своей суммой функции .

Поскольку ряд (1) сходится равномерно на к функции , имеем для его коэффициентов представление :

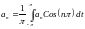
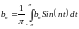
Замечание.

а.) Если функция периода 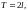является чётной, то так же как и в случае 2π периодической из Леммы следует, что:

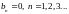
б.) Если нечётная, то для неё:

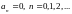
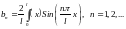
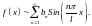
t

§8. Ряд Фурье непериодической функции.

B(b,π)

A(a,-π)

L

b

a

-π

π

x

Пусть задана на , 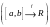. Отобразим на .

Уравнение по двум (..)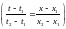 имеет вид:

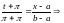
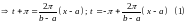
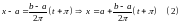
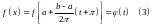
Функция задана на . Разложим её в ряд Фурье:

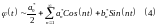
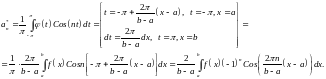
Замечание:

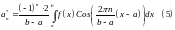
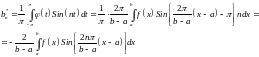(6)

Переходя в (4) от к , получим

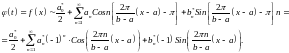
Учитывая знаки при 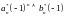получим, что:

То:

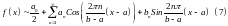
Формулы (5’), (6’) задают коэффициенты Фурье непериодической функции, а (7) – её разложение в ряд Фурье на .

Пример. Разложить в 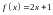на 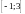в ряд Фурье.

-1

7

3

-1

x

y

Решение.

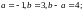
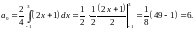
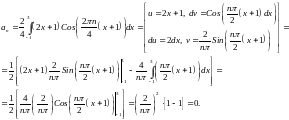
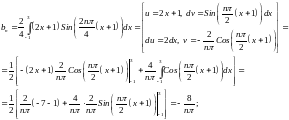
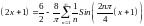
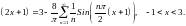
Рассмотрим схему разложения функции 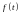в ряд Фурье в самом общем случае.

Задача. Разложить в ряд Фурье функцию , заданную на промежутке

Общий порядок решения поставленной задачи сводится к следующему:

1. Построение графика заданной в функции и проверка выполнения условий Дирихле.

2. Периодическое продолжение функции периода 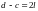на всю числовую ось.

3. Вычерчивание эскиза графика полученной функции.

4. Определение характера симметрии функции: чётность, нечётность и т.п.

5. Выписывание в общем виде ряда Фурье функции :

6. Вычисление коэффициентов по формулам: