Свойства сходящихся последовательностей
Теорема 1 (о единственности предела). Предел сходящейся последовательности определен однозначно.
Проведем доказательство от противного: пусть числа и
являются пределами последовательности
и
.
Возьмем
.
,
.
Пусть
.
Тогда
,
т. е.
.
Абсурдность
полученного неравенства доказывает,
что
.
Впрочем, теорему
о единственности предела можно доказать,
используя понятие
-окрестности
точки:
,
но
.
Теорема 2. Сходящаяся последовательность ограничена.
Пусть
.
Взяв
,
найдем
такое, что
выполняется неравенство
.
Тогда для этих
.
Если положить
,
то получим
,
то есть последовательность
ограничена.
Замечание. Ограниченность – необходимое условие сходимости последовательности, но не достаточное.
Пример. Последовательность ограничена, но не является сходящейся.
Теорема 3 (о сохранении знака сходящейся последовательности).
Если
,
,
то существует такое натуральное число
,
что
.
При этом, если
,
то
,
если
,
то
.
Возьмем
и найдем
такое, что
выполняется неравенство
.
Тогда,
.
Е
x
,
е
сли
же
,
то
.
Следовательно,
.
Предельный переход в неравенствах
Пусть
задано некоторое высказывание
(например,
).
Будем говорить, что
истинно для всех
,
начиная с некоторого номера, или
верно для всех достаточно больших
,
и писать
или
,
если
такое, что
,
следующего за
,
справедливо высказывание
,
то есть:
.
Высказывание будем называть асимптотическим.
Теорема
о неравенстве пределов (ТНП).
Пусть
,
.
Тогда: 1) если
,
то
;
2) если
,
то
.
Пусть ,
.
Возьмем
.
Так как
,
то
,
то есть
.
Так как
,
то
,
то есть
.
Пусть
.
Тогда для
,
то есть
.
2. Доказательство
проведем от противного. Пусть
,
тогда согласно пункту 1
,
то есть
По условию
начиная с некоторого
.
Таким образом, для числа
выполняются неравенства
и
.
Абсурд! Значит,
.
Замечание.
Из неравенства
не следует неравенство
.
В самом деле, пусть
,
,
,
т.е.
.
Следствия из ТНП:
если , то ;
если
,
то
;если
,
то
.
Теорема о пределе
промежуточной последовательности
("теорема
о двух милиционерах"). Пусть
и
.
Тогда
.
Действительно,
,
.
Пусть . Тогда и выполняются неравенства:
и
.
Таким образом,
,
то есть
и, следовательно,
.
Следствие.
Если
,
то
.
Доказательство
следствия вытекает из того, что
и из оценки
.
Замечание.
Обратное утверждение неверно. Рассмотрим
последовательность
.
Ясно, что
,
но
не существует.
Бесконечно малые и бесконечно большие последовательности
Определение.
Последовательность
называется бесконечно малой (б. м.),
если
.
В этом случае будем писать
.
Символ
читается "о-малое
от единицы".
Определение.
Последовательность
называется бесконечно большой (б. б.),
если
.
В этом случае пишут
(
).
Если
,
то пишем
.
Пример.
Пусть
.
Заметим, что эта последовательность не
сходится ни к
,
ни к
.
В этом случае
,
поэтому
,
т. е. последовательность сходится к
.
Определение.
Последовательность
называется ограниченной, если существует
такое число
,
что
для всех
.
Заметим, что это определение эквивалентно приведенному выше (см. п. "Числовые последовательности").
Отметим основные свойства б. м. последовательностей.
Теорема 1.
Пусть
– б. м. последовательность,
– ограниченная последовательность,
тогда последовательность
– бесконечно малая, т.е.
.
Так как
,
то
.
Положим
,
где
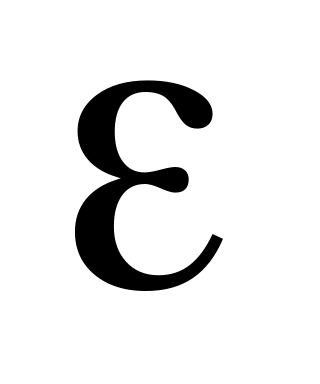– произвольное положительное число.
Т. к.
– б. м. последовательность, то
.
Тогда
,
т.е.
.
Теорема 2.
,
тогда и только тогда, когда
,
где
.
Необходимость.
Пусть
.
Тогда
.
Обозначим
,
тогда
и
.
Достаточность.
Пусть
,
где
.
Тогда
,
то есть
,
а это значит, что
.
Следствие.
.
В частности,
.
Теорема 3.
Пусть
– бесконечно малая последовательность
и
.
Тогда
– бесконечно большая последовательность.
Действительно,
.
Так как
.
Пусть
.
Возьмем
,
.
Теперь по заданному
находим
такое, что
для
.
Тогда для этих
имеем
,
т.е.
.
Теорема 4. Если
– бесконечно большая последовательность
и
,
то
– бесконечно малая последовательность.
Доказательство аналогично предыдущему.
Упражнения.
Если последовательности
,
– бесконечно малые, то бесконечно малыми
являются и последовательности
,
,
,
т.е.
