Решение задач линейного программирования геометрическим методом

Графический метод решения ЗЛП основан на следующих утверждениях.

Система ограничений ЗЛП геометрически представляет собой выпуклый многоугольник или выпуклую многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы.

Целевая функция Z = c₁x₁ + c₂x₂ геометрически изображает семейство параллельных прямых, перпендикулярных вектору нормали N(с₁,с₂). Эти прямые называются линиями уровня.

Линия уровня – это прямая, вдоль которой целевая функция принимает фиксированное значение.

Теорема. При перемещении линии уровня в направлении вектора нормали N значение целевой функции возрастает, в противоположном направлении - убывает.

Алгоритм графического метода решения ЗЛП.

В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;

найти полуплоскость решения каждого неравенства системы (обозначить стрелками). Для определения полуплоскости необходимо выбрать любую контрольную точку, не лежащую на данной прямой. Подставить ее координаты в систему ограничений. Если неравенство выполняется, то нужно выбрать полуплоскость, содержащую контрольную точку. Если неравенство не выполняется нужно выбрать полуплоскость, не содержащую контрольную точку. В качестве контрольной точки рекомендуется выбирать точку с координатами (0;0);

найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;

построить вектор нормали N. Начало вектора нормали в точке с координатами (0;0), конец вектора в точке с координатами (с1, с2);

через начало координат построить линию уровня, перпендикулярно к вектору нормали;

перемещать линию уровня параллельно самой себе по области решения в угловые точки, достигая max f при движении вектора N и достигая точки «выхода» (min f при движении достигая точки «входа»);

найти координаты точки max (min). Для этого необходимо решить систему уравнений прямых, которые пересекаются в этой точке или определить координаты по графику;

вычислить значение целевой функции в этой точке (ответ).

Задача. Решить графическим методом следующую задачу линейного программирования:

.

1. Найдем общую часть всех полуплоскостей решений. Получим, что область допустимых решений представляет собой четырехугольник

2. Построим вектор-градиент .

3. Построим прямую , проходящую через начало координат перпендикулярно .

4. Перемещаем прямую параллельно и пересечем ОДР. Последнее пересечение с ОДР будет в точке , которая соответствует максимуму целевой функции.

5.Определим координаты точки , решая систему .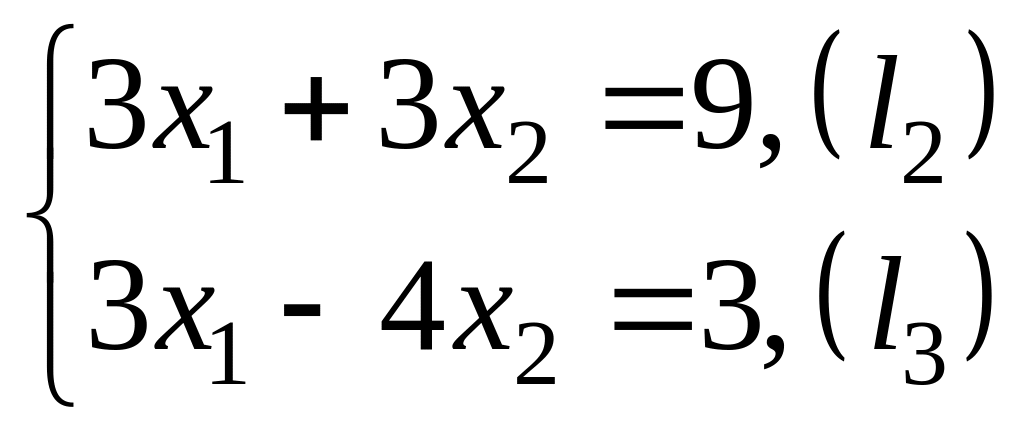

Подставив координаты точки в целевую функцию, получим

:

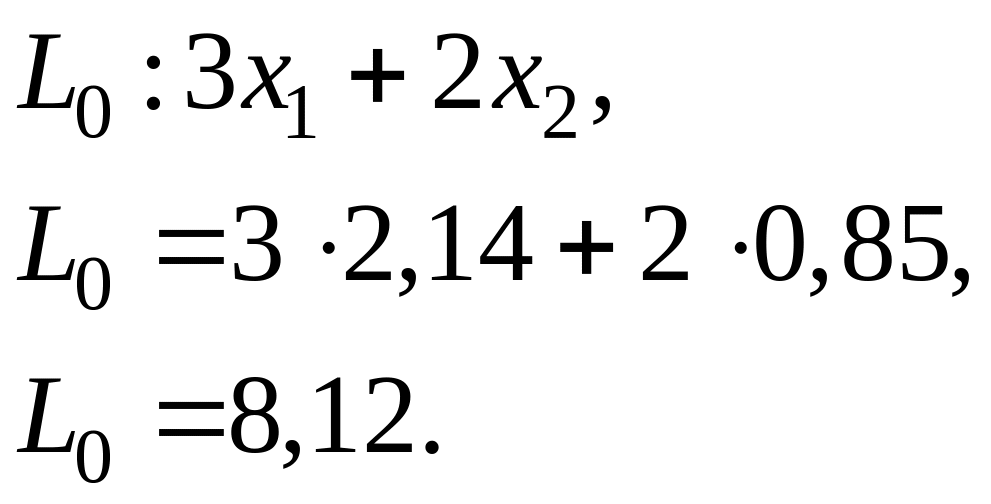
Точка С (2,14; 0,85) является точкой максимума

Ответ: F_max= 8,12 при x (2,14; 0,85)

Симплексный метод решения задач линейного программирования

Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, то трудно представить наглядно графически область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода (метода последовательных улучшений). По определенному правилу находится первоначальный опорный план (некоторая вершина области ограничений). Проверяется, является ли план оптимальным. Если да, то задача решена. Если нет, то переходим к другому, улучшенному плану – к другому базису. Значение целевой функции в новом базисе (в новой вершине) заведомо лучше, чем в предыдущем. Алгоритм перехода осуществляется с помощью некоторого вычислительного шага, который удобно записывать в виде таблиц, называемых симплекс-таблицами. Так как вершин конечное число, то за конечное число шагов мы приходим к оптимальному решению.

Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т.е. имеющих базис (Базисным называется решение, соответствующее нулевым значениям свободных переменных), положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.

Рассмотрим алгоритм решения задачи симплекс-методом на конкретном примере задачи о планировании производства, предварительно построив модель и приведя ее к каноническому виду.

Задача (о планировании производства изделий).

Для изготовления изделий А и В склад может отпустить сырья не более 80 единиц. Причем на изготовление изделия А расходуется две единицы, а изделия В – одна единица сырья. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий А требуется изготовить не более 50 шт., а изделий В – не более 40 шт. Причем прибыль от реализации одного изделия А – 5 тыс. руб., а от одного изделия В – 3 тыс. руб.

Построим математическую модель, обозначив за – количество изделий А в плане, за – количество изделий В, тогда система ограничений будет выглядеть следующим образом:

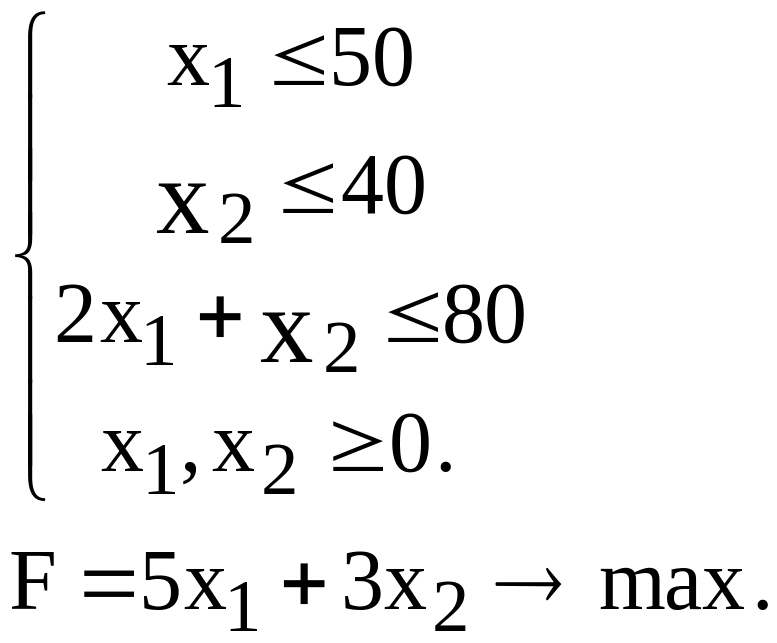
Приведем задачу к каноническому виду, введя дополнительные переменные