
- •Практическая работа По математике Тема: «Преобразование графиков функции»
- •Преобразование графиков Параллельный перенос
- •Отображение
- •Деформация (растяжение и сжатие) графика
- •Отражение
- •Отражение относительно осей и точек
- •Логарифмическая функция, ее свойства и график Теория:
- •Определение тригонометрических функций как решений дифференциальных уравнений
- •Определение тригонометрических функций как решений функциональных уравнений
- •Определение тригонометрических функций через ряды
- •Производные и интегралы
- •Значения тригонометрических функций для некоторых углов
- •Значения тригонометрических функций нестандартных углов
- •Свойства тригонометрических функций Простейшие тождества
Отражение относительно осей и точек
Пусть
имеется график функции y = f (
x ). Чтобы получить график функции,
симметричный данному относительно оси
OX , нужно умножить значение функции в
каждой точке области определения на
–1. Алгебраически это задается системой:

Графики функций y = f ( x ) и y = – f ( x ) симметричны относительно оси абсцисс.
Аналогичным
образом отражается график относительно
оси OY :
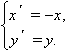
Графики функций y = f ( x ) и y = f (– x ) симметричны относительно оси ординат.
Отражение
графика относительно начала координат
сводится к отражению сначала относительно
оси абсцисс, затем относительно оси
ординат и задается системой уравнений
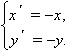

Модель 1.15. Отражение графиков относительно осей и точек.
Симметричными относительно начала координат являются графики функций y = f ( x ) и y = – f (– x ). Более сложным является вопрос о симметрии графиков относительно произвольных вертикальных и горизонтальных осей. Справедливы следующие утверждения.
Графики функций y = f ( x ) и y = 2 b – f ( x ) симметричны относительно горизонтальной оси y = b .
Графики функций y = f ( x ) и y = f (2 a – x ) симметричны относительно вертикальной оси x = a .
Системы
уравнений, соответствующие этим
преобразованиям, выглядят так:
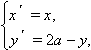 и
и
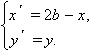
Наконец,
отражение графика относительно
произвольной точки ( a , b ) задается
сначала отражением относительно
горизонтальной оси y = b , затем
отражением относительно вертикальной
оси x = a :
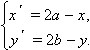
Графики функций y = f ( x ) и y = 2 b – f (2 a – x ) симметричны относительно точки ( a ; b ).
Симметрия относительно прямой
Пусть
g — фиксированная прямая (рис. 191). Возьмем
произвольную точку X и опустим перпендикуляр
АХ на прямую g. На продолжении перпендикуляра
за точку А отложим отрезок АХ', равный
отрезку АХ. Точка X' называется симметричной
точке X относительно прямой g.
 Если
точка X лежит на прямой g, то симметричная
ей точка есть сама точка X. Очевидно, что
точка, симметричная точке Х' есть точка
X.
Если
точка X лежит на прямой g, то симметричная
ей точка есть сама точка X. Очевидно, что
точка, симметричная точке Х' есть точка
X.
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F' называются симметричными относительно прямой g (рис. 192).
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.
Например,
прямые, проходящие через точку пересечения
диагоналей прямоугольника
параллельно его сторонам, являются
осями симметрии прямоугольника (рис.
193). Прямые, на которых лежат диагонали
ромба, являются его осями симметрии
(рис. 194).
 Теорема
9.3. Преобразование симметрии относительно
прямой является движением.
Теорема
9.3. Преобразование симметрии относительно
прямой является движением.
 Доказательство.
Примем данную прямую за ось у декартовой
системы координат (рис. 195). Пусть
произвольная точка А (х; у) фигуры F
переходит в точку А' (х'; у') фигуры F'. Из
определения симметрии относительно
прямой следует, что у точек А и А' равные
ординаты, а абсциссы отличаются только
знаком:
Доказательство.
Примем данную прямую за ось у декартовой
системы координат (рис. 195). Пусть
произвольная точка А (х; у) фигуры F
переходит в точку А' (х'; у') фигуры F'. Из
определения симметрии относительно
прямой следует, что у точек А и А' равные
ординаты, а абсциссы отличаются только
знаком:
х'= —х. Возьмем две произвольные точки А(х1; y1) и В (х2; y2)- Они перейдут в точки А' ( — х1, y1) и В' ( —x2; y2).
Имеем: AB2 = (x2 - x1)2 + (y2 - y1)2 A'B'2 =(-x2 + x1)2+(y2-y1)2. Отсюда видно, что АВ=А'В'. А это значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.
Параллельный перенос и растяжение графиков
Если известен график функции y = f(x), то с его помощью легко получить график функции вида y = kf(ax + b) + l. Опишем это построение по этапам. Из графика функции f(x): 1) график функции f(ax), a > 0, получается сжатием графика f(x) вдоль оси x в a раз ("сжатие" с коэффициентом a, 0 < a < 1, является растяжением в 1/a раз); 2) график функции f(-x) - преобразованием симметрии относительно оси y; 3) график функции f(x + b) - переносом параллельно оси x на отрезок длины |b| влево, если b > 0, и вправо, если b < 0; 4) график функции kf(x), k > 0, - растяжением вдоль оси y в k раз ("растяжение" с коэффициентом k, 0 < k < 1, является сжатием в 1/k раз); 5) график функции -f(x) - преобразованием симметрии относительно оси x; 6) график функции f(x) + l - переносом параллельно оси y на отрезок длины |l| вверх, если l > 0, и вниз, если l < 0. Применив эти операции, из графика функции f(x) можно получить график функции
kf(ax + b) + l
![]()
![]() +
l,
a
+
l,
a
![]() 0.
0.
Для этого согласно указанному выше надо последовательно построить графики функций
f(ax), = f(ax + b), kf(ax + b), kf(ax + b) + l
(на рис. 42 схематически изображено построение графика функции kf(ax + b) + l в случае, когда a > 0, b > 0, k > 0, l > 0).
|
|
|
Показательная функция, ее свойства и график
Цель изучения параграфа — введение понятия показательной функции; демонстрация применения знаний о свойствах показательной функции к решению прикладных задач.
Для обоснования свойств показательной функции необходимо знание материала IV главы учебника о свойствах степени. Поэтому повторение этих свойств, компактно сформулированных в начале параграфа, можно провести в ходе устного выполнения следующих упражнений:
1. Представьте в виде степени числа a > 0:
1) a 3 a −5 a 1 2 ; 2) a 3 2 : a 2 ; 3) a 1 3 ⋅a a 2 3 ; 4) ( a 3 ) 3 ; 5) ( a 6 ) 1 3 ⋅ a −2 .
2. Найти значение выражения: 1) (2π) 7 2 8 π 7 ; 2) ( 2 3 ) 6 ⋅ 2 −4 ⋅ 3 5 .
3. Сравнить с единицей: 1) 1,3 3 ; 2) 0,7−5.
4. Сравнить: 1) 0,97 и 0,96; 2) π 1 2 и π 1 3 .
Полезно повторить с учащимися выявление свойств функции по ее графику. С этой целью можно, например, используя график функции на рисунке 13, найти:
1) значения аргумента, при которых значение функции равно нулю;
2) координаты точки пересечения графика с осью ординат;
3) значения аргумента, при которых функция принимает положительные (отрицательные) значения;
4) промежутки возрастания (убывания) функции.
Введение понятия показательной функции, обоснование ее свойств, построение графиков и исследование поведения графиков, их особые точки рассматриваются в последовательности, предложенной учебником. После этого решается задача 1.
Разбор решения этой задачи позволит учащимся выполнить упражнения 6 и 7 без построения графиков функции.
Задачу 2 желательно рассмотреть и с учащимися общеобразовательных классов. Они могут не производить вычисления на микрокалькуляторах, а принять на веру расчеты, предложенные в учебнике.
Задачу 3, носящую исследовательско-прикладной характер, рекомендуется внимательно рассмотреть с учащимися профильных классов. Они должны использовать микрокалькуляторы для выполнения расчетов при решении задачи 2, а также при выполнении упражнений 17—20.
При желании учитель в профильных классах может давать учащимся задание по написанию программы вычислений значений выражений на микрокалькуляторе. Так, например, для решения задачи 2 вычисления на инженерном микрокалькуляторе МК-51 можно провести по следующей программе:
365 ÷ 14 = х→Π 0,5 y x Π→х = × 8 =

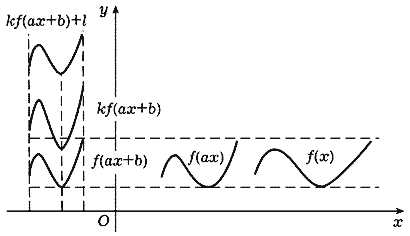 Рис.
42
Рис.
42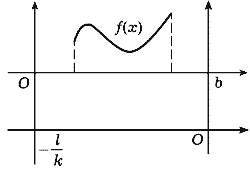 Рис.
43
Рис.
43