Демонстрационный вариант теста

1. Даны векторы и . Вектор имеет координаты

1) 2) 3) 4)

2. Даны векторы и . Скалярное произведение этих векторов равно

1) 4 2) –2 3) –8 4)

3. Даны матрицы и . Матрица равна

1) 2) 3) 4)

4. Даны матрицы и . Матрица равна

1) 2) 3) 4)

5. Определитель равен

1) 2 2) –2 3) 17 4) –14

6. Определитель равен

1) –16 2) 0 3) –1 4) –4

7. Определитель равен

1) 6 2) 0 3) –6 4) 1

8. Главный определитель системы линейных алгебраических уравнений

записывается в виде

1) 2) 3) 4)

9. Побочный (вспомогательный) определитель системы линейных алгебраических уравнений

записывается в виде

1) 2) 3) 4)

10. Значение переменной в системе линейных алгебраических уравнений

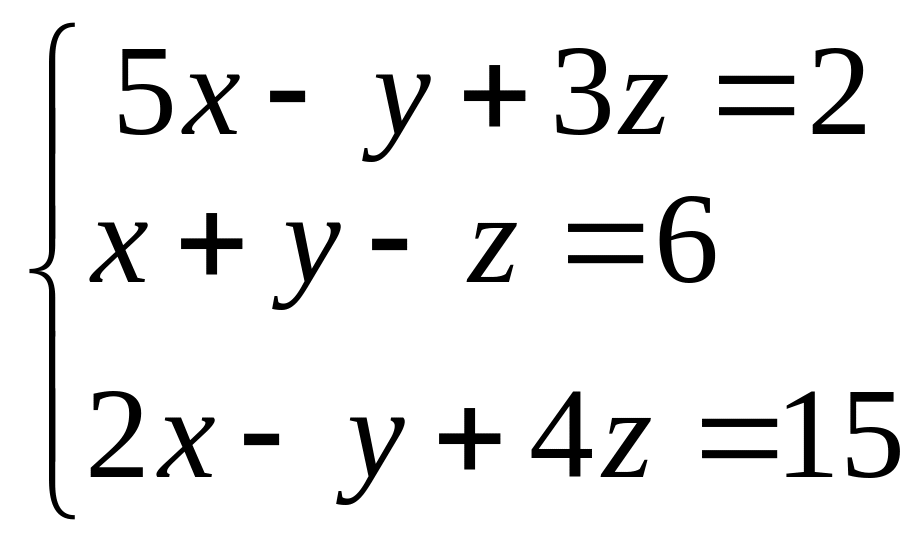
находится по формуле

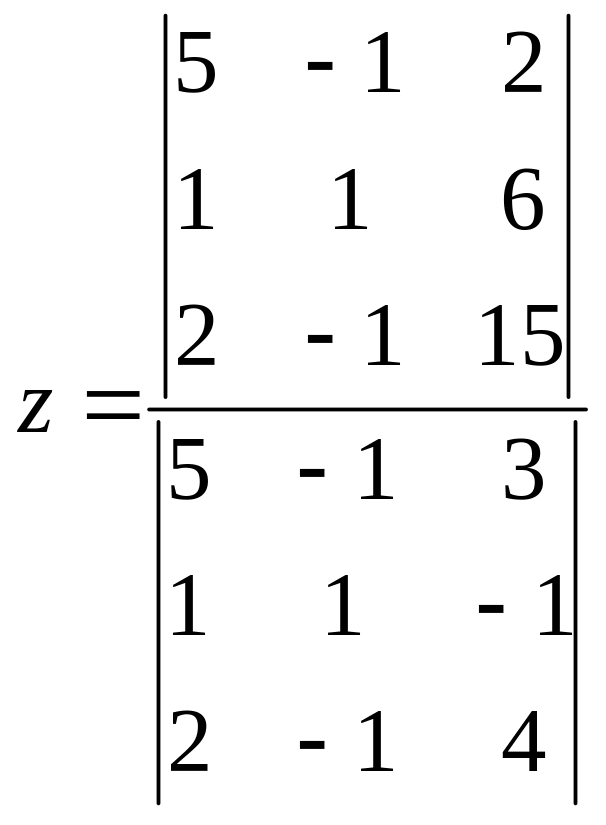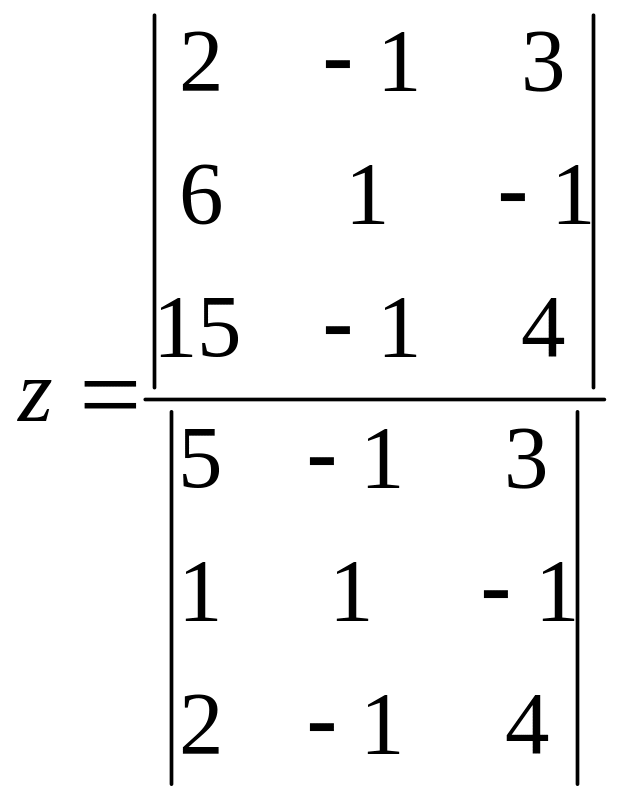1) 2) 3)

4)

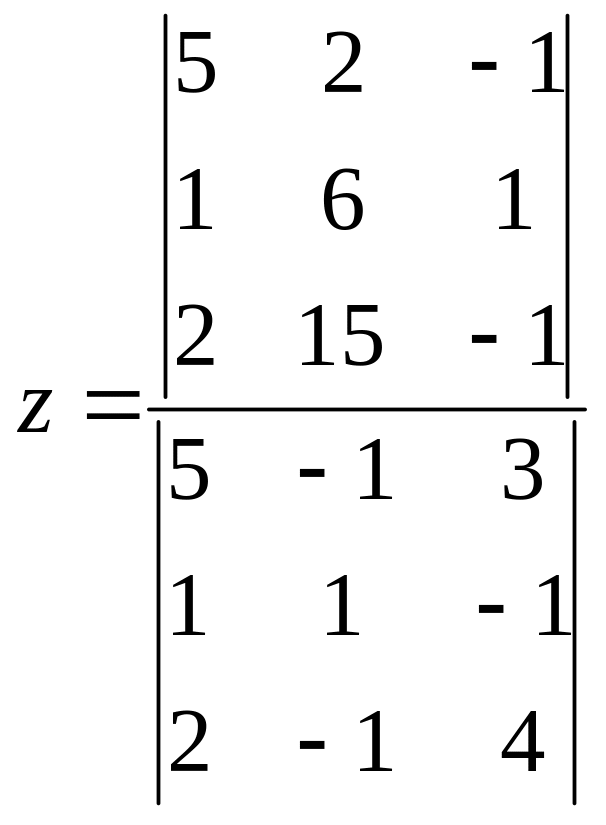
11. Система линейных алгебраических уравнений

1) не имеет решений 2) имеет бесконечно много решений

3) имеет одно решение 4) имеет ровно два решения

12. Прямые и на плоскости хОу

1) не пересекаются

2) совпадают

3) пересекаются только в точке (2; 2)

4) пересекаются только в точке (0; –2)

13. Прямая параллельна прямой

1) 2) 3) 4)

14. Прямая пересекается с прямой

1) 2)

3) 4)

15. Окружность имеет центр О и радиус r

1) 2) 3) 4)

16. Плоскости и

1) не пересекаются

2) совпадают

3) пересекаются только по одной прямой

4) пересекаются только по двум прямым

17. Плоскости принадлежит точка

1) (2; 2; 5) 2) (1; 1; 0) 3) (2; 3; 4) 4) (0; 1; 4)

18. Прямая и плоскость

1) не пересекаются

2) расположены так, что прямая лежит в плоскости

3) пересекаются только в одной точке

4) пересекаются только в двух точках

19. Среди прямых а) , б) , в) , г)

асимптотами графика функции являются

1) б) и в) 2) а) и г) 3) только в) 4) только г)

20. Производная функции равна

1) 2)

3) 4)

21. Производная функции равна

1) 2)

3) 4)

22. Производная неявно заданной функции равна

1) 2)

3) 4)

23. Касательная к графику функции , проведенная в точке с проходит через точку

1) (2; 9) 2) (0; 7) 3) (1; 4) 4) (1; –5)

2 4. На рисунке изображена часть графика функции . Для выполнено

1)

2)

3)

4)

25. равен

1) –1,2 2) 0 3) 1 4) –1

26. равен

1) –5 2) 4 3) 5 4) 0

27. равен

1) 0 2) 1 3) 4) –1

28. равен

1) 0 2) 3) 1 4) –1

29. Разность наибольшего и наименьшего значений функции на отрезке равна

1) –32 2) 32 3) 0 4) 3

30. Точка движется прямолинейно по закону , где — координата точки, а — время движения. Координата будет наименьшей в момент времени, равный

1) 10 2) 2 3) 0 4) 1

31. равен

1) 2)

3) 4)

32. равен

1) 2) 3) 0 4) 6

33. Площадь S фигуры, ограниченной линиями равна

1) 2) 3 3) 4) 3,5

34.

1) равен 3 2) равен 5 3) расходится 4) равен 5/12

35. Решением дифференциального уравнения является

1) 2)

3) 4)

36. Решением дифференциального уравнения является

1) 2) 3) 4)

37. График функции, являющейся решением задачи Коши , пересекает ось Оу в точке

1) (0; –2) 2) (0; –1) 3) (0; 1) 4) (0; 3)

38. Общим решением дифференциального уравнения является

1) 2)

3) 4)

39. Решением задачи Коши является функция

1)

2)

3)

4)

40. В классе 12 мальчиков и 9 девочек. Дежурят по классу двое: мальчик и девочка. Назначить дежурных можно

1) 108 способами 2) 12 способами 3) 9 способами 4) 21 способом

41. Студент забыл последние две цифры пятизначного номера телефона. Количество вариантов набора номера наугад равно

1) 100 2) 10 3) 20 4) 81

42. Из цифр 1, 2, 3, 4, 5 можно составить следующее число различных пятизначных чисел при условии, что цифры могут повторяться

1) 3125 2) 120 3) 25 4) 625

43. В классе 23 человека. Каждый день по классу дежурят трое. Назначить дежурных можно

1) 10626 способами 2) 23 способами 3) 12167 способами

4) 1771 способом

44. Вероятность того, что при бросании игральной кости выпадет число очков, меньшее 5, равна

1) 2/3 2) 1/3 3) 5/6 4) 3/4

45. Бросается игральная кость. Рассматриваются события:

А — выпало менее 2 очков;

В — выпало менее 3 очков;

С — выпало четное число очков;

D — выпало более 4 очков;

Е — выпало 5 очков.

Совместными являются события

1) А, С 2) А, D 3) В, D 4) С, D

46. Событие А называется невозможным, если в результате данного испытания

1) оно не наступает никогда

2) оно наступает всегда

3) оно может наступить, а может и не наступить

4) оно может наступить только 2 раза подряд

47. Пересечением событий А и В называется событие, состоящее в том, что в результате некоторого испытания

1) наступает событие А и событие В одновременно

2) наступает событие А или событие В

3) не наступает ни одно из этих событий

4) наступает только событие А

48. Если события А и В являются независимыми, а событие С есть пересечение А и В, то Р(С) равна

1) 0 % 2) 100 % 3) Р(А)·Р(В) 4) Р(А)+Р(В)

49. Объединение события А и события, противоположного А, есть

1) достоверное событие 2) невозможное событие

3) событие А 4) событие, противоположное А

50. Ниже приведена таблица количества испытаний n и количества k наступления при этом события А

n	10	100	200	1000
k	3	29	59	291

Статистическая вероятность наступления события А при одном испытании приближенно равна

1) 0,12 2) 0,29 3) 0,39 4) 0,41

51. В отрезок [1; 9] наудачу бросается точка. Вероятность того, что эта точка попадет при этом и в отрезок [2; 3] равна

1) 0,2 2) 0,125 3) 0 4) 0,5

52. Вероятность наступления события А при одном испытании равна 0,7. Было проведено 10 независимых повторных испытаний. Вероятность того, что событие А наступило при этом ровно 4 раза рассчитывается по формуле:

1) 2)

3) 4)

53. Дан закон распределения дискретной случайной величины Х.

Возможные значения Х	2	4	8	16
Вероятности Р(Х)	0,1		0,6	0,1

Вероятность того, что данная случайная величина примет значение 4, равна

1) 0,2 2) 1 3) 0,5 4) 0,3

54. Дана дискретная случайная величина Х с математическим ожиданием 8,2 и среднеквадратическим отклонением 0,4. В какой промежуток с вероятностью не менее 8/9 попадет Х при очередном испытании?

1) [7; 9,4] 2) [7; 9] 3) [7,5; 8,5] 4) [7,7; 8,7]

55. Даны случайные величины:

1) Время решения некоторой задачи;

2) Количество ошибок в тесте;

3) Длина прыжка с трамплина;

4) Длина стопы;

5) Количество человек в группе, отдавших предпочтение желтому цвету;

6) Расстояние от центра мишени до точки попадания при одном выстреле;

7) Время подготовки к ответу на экзамене.

Непрерывными случайными величинами являются

1) 1, 3, 4, 6, 7 2) только 1 и 6 3) 2, 5 4) только 1, 2 и 5

56. Даны случайные величины:

1) Время решения некоторой задачи;

2) Количество решенных задач в контрольной работе;

3) Оценка на экзамене;

4) Время выполнения теста;

5) Количество человек в группе, отдавших предпочтение желтому цвету;

6) Расстояние от центра мишени до точки попадания при одном выстреле;

7) Номер желтого цвета при расположении семи цветов по убыванию предпочтения.

Дискретными случайными величинами являются

1) только 2 2) только 2 и 3 3) 1, 4, 6 4) 2, 3, 5, 7

57. Все значения непрерывной случайной величины Х попадают в промежуток [1; 5]. Вероятность того, что в результате испытания Х примет значение, меньшее 6, равна

1) 1 2) 0 3) 0,5 4) 0,7

58. Все значения непрерывной случайной величины Х попадают в промежуток [10; 50]. Вероятность того, что в результате испытания Х примет значение, меньшее 7, равна

1) 0 2) 1 3) 0,5 4) 0,25

59. Если две непрерывные случайные величины Х и Y распределены по нормальному закону c одинаковыми дисперсиями, но разными математическими ожиданиями, то графики плотностей вероятности

1) по форме и высоте одинаковы, но смещены вдоль горизонтальной оси

2) имеют максимумы разной высоты в одной и той же точке

3) полностью совпадают

4) имеют максимумы разной высоты в разных точках

60. Выборка задана распределением частот:

Значение признака Х	1	3	4	6
Частота проявлений значения	10	20	20	50

Выборочное среднее равно

1) 4,5 2) 4 3) 3,5 4) 5