3. Дворівнева система вимірювання факторів

При дворівневій системі змінювання факторів (а саме такі системи найчастіше використовуються в експериментах) число всіх точок факторного простору дорівнює (базова точка, в околі якої шукають лінійну апроксимацію функції відгуку, до уваги не береться, оскільки в цій точці експеримент не проводиться).

Нехай в експерименті реалізуються всі можливі поєднання рівнів факторів, тобто . Такий експеримент називається повним факторним експериментом (планом). Повний факторний експеримент зручно подавати у вигляді матриці планування. Геометрично повний факторний план при можна зобразити у вигляді куба, центр якого відповідає точці основного рівня факторів, а координати вершин задані умовами спроб. При повний факторний план геометрично означає n-вимірний гіперкуб.

4. Повні факторні плани та їхні властивості

Повні факторні плани мають важливі для планування експериментів властивості:

симетричність плану відносно центра експерименту

де — значення рівня i-го фактора в j-й спробі;

нормування плану

ортогональність плану — скалярні добутки векторів-стовпців матриці планування дорівнюють нулю:

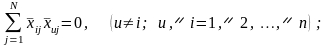
рототабельність (від лат. roto — обертаюсь) плану означає, що точність передбачення значення функції відгуку однакова на рівних відстанях від центра експерименту і не залежить від напряму руху (в рототабельних планах точки факторного простору, що використовуються для спроб, лежать на поверхні сфери, центром якої є точка основного рівня).

Повні факторні плани дають змогу встановити вплив на функцію відгуку не тільки окремо кожного фактора, а і їх комбінації, тобто дослідити так званий ефект взаємодії. Для цього до матриці планування додатково вносять вектори-стовпці, що містять значення комбінацій рівнів факторів. Крім того, з метою спрощення обробки даних до матриці планування введено деякий фіктивний фактор , що набуває єдиного значення +1. Зауважимо також, що матриця планування з ефектами взаємодії зберігає перелічені властивості пов­них факторних планів.

Слід зазначити, що в умовах, коли відсутній вплив ефектів взаємодії на функцію відгуку, коефіцієнти регресії в рівнянні (9.4), що стоять при нелінійних членах, малі порівняно з коефіцієнтами при лінійних членах. Це означає, що функція відгуку може описуватися поліномом першого ступеня. У такому разі необхідно визначити невідомих коефіцієнтів . Оскільки в повному факторному плані виконується спроб, то з огляду на умову здобуті дані для багатофакторних планів будуть надмірними. Тому для оцінок коефіцієнтів у лінійних апроксимуючих поліномах використовуються дробові факторні плани, у яких число спроб менше за число точок у факторному просторі. Наприклад, коли в повному двофакторному плані знехтувати ефектом взаємодії факторів Х₁ і Х₂, то вектор-стовпець матриці планування, у якому розміщені елементи добутку , можна використати для запису рівнів третього фактора . Здобутий при цьому дробовий факторний план матиме властивості симетричності, нормованості, ортогональності, рототабельності