2.2. Различение детерминированных сигналов

2.2.1. Статистические критерии различения детерминированных сигналов.

Для того чтобы задача поиска, или синтеза, оптимальных правил различения сигналов обрела матема­тическую содержательность, необходимо, прежде всего, задаться некоторым формальным показателем (критерием) качества различения, т. е. количественной мерой, сумми­рующей ущерб, наносимый ошибочными решениями.

В тех задачах, которые удается свести к проверке простых гипотез, продуктивным оказывается критерий минимума среднего риска, называемый также критерием Байеса. Для того чтобы наиболее наглядно ввести связан­ную с ним систему понятий и терминов, обратимся к конкретному примеру различения М детерминированных сигналов s₀(t), S₁(t), ..., S_M-1(t), на фоне помех с полностью заданным статистическим описанием, т. е. с точно извест­ной ПВ любой размерности или с точно известным функционалом ПВ. В рамках такой модели различения ПВ любой размерности или функционал ПВ наблюдаемого колебания y(t) при условии, что в y(t) входит сигнал с номером i, - некоторая вполне определенная функция, вид которой зависит лишь от номера i. При этом имеется M классов, содержащих по одному распределению, т. е. различение сигналов состоит в проверке простых гипотез.

Предположим, что известна вероятность p_i присутствия в y(t) сигнала s_i(t). Эту вероятность называют априорной (доопытной), поскольку она отражает сведения, которыми располагает наблюдатель, еще не имея в распоряжении реализации y(t), и показывает, насколько часто при длительной эксплуатации изучаемой системы можно ожи­дать появления s_i(t) в y(t). Для систем М-ичной цифровой связи, например, вероятность p_i характеризует среднюю частоту, с которой s_i(t) посылается в канал. Очевидно, вероятность p_i, - можно назвать и априорной вероятностью истинности Н_i записав p_i = P(Н_i ). При этом р_i подчинены условию нормировки ибо события H₀,..,Н_M-1 составляют полную группу несовместных событий.

Предположим, что p_ik = P(Н_k/H_i) - условная вероят­ность перепутывания i-го сигнала с k-м, т. е. принятия решения - о присутствии s_k(t) в y(t) при условии, что истинна Н_i [в y(t) содержится s_i(t)]. Следовательно, множество вероятностей p_ik при i≠k составляет набор условных вероятностей всех ошибочных решений. Эти вероятности для любого фиксированного способа различе­ния сигналов можно вычислить, так как помехи считаются полностью статистически заданными.

Введем М² неотрицательных величин П_ik, каждая из которых характеризует риск (потери, ущерб) от перепутывания i-го сигнала с k-м. При этом правильные решения считаются не наносящими ущерба, так что П_ii = 0. Для наглядности можно считать П_ik некими денежными штра­фами, уплачиваемыми за ошибки.

В каждой отдельной попытке различения сигналов итог (решение) оказывается случайным событием, а по­этому случайным будет и значение риска. Очевидно, безусловную вероятность того, что риск окажется равным П_ik, по теореме умножения вероятностей можно найти как P(H_i)P( /H_i) = p_i p_ik , поэтому математическое ожидание риска или средний риск

. (2.1)

Критерий Байеса, или минимального среднего риска, предписывает добиваться минимума (11). Различитель, оптимальный по этому критерию (байесовский различитель), при длительной эксплуатации будет наиболее «эконо­мичным» из всех, поскольку сумма штрафов за ошибки у него окажется наименьшей.

Хотя задание рисков П_ik (часто и априорных вероят­ностей) достаточно произвольно, практическая ценность критерия Байеса чрезвычайно велика, так как он, обобщая ряд других критериев, позволяет получить универсальный ответ на вопрос о наилучшей стратегии различения сигналов. Предположим, например, что, не имея объектив­ных данных для назначения всех рисков, разработчик стремится лишь к тому, чтобы различитель как можно реже ошибался, т. е. чтобы полная вероятность ошибки p_ош

, была минимальной, где i≠k. (2.2)

Такой критерий качества, называемый критерием идеального наблюдателя или критерием Котельникова, его можно рассматривать как частный случай байесовского, положив в (11), П_ik=П, i≠k, где П - произвольная неотрицательная константа. При этом и минимизация среднего риска рав­носильна минимизации (2.2).

В случае если затруднение вызывает задание не только рисков, но и априорных вероятностей, например, для радиолокационного обна­ружения. Тогда определить полную вероятность ошибки нельзя, но можно предложить вполне удовлетворительный критерий качества - критерий минимума суммы условных вероятностей ошибок

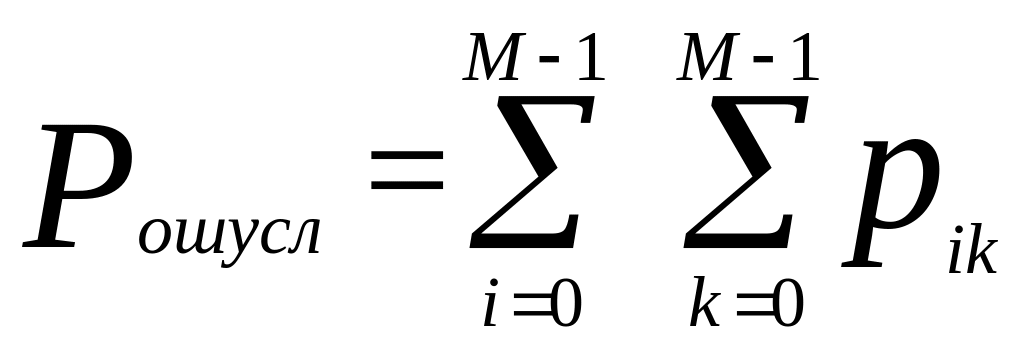, при i≠k. (2.3)

Легко убедиться, что это частный случай байесовского критерия, в котором П_ik=П, i≠k, pi=l/M; i = 0, 1, ..., М-1. Действительно, после "этих подстановок (2.1) примет вид , указывающий на идентичность задач мини­мизации и

В частном случае М=2, ,s₀(t) = 0 рассматриваемая задача переходит в обнаружение детерминированного сигнала S₁(t) на фоне помех с известным статистическим описанием. При этом условные вероятности р₀₁= Р( |H₀) и p₁₀ = Р( |H₁) на статистическом языке называют веро­ятностями ошибок первого и второго рода. Согласно терминологии, принятой в радиоэлектронике, эти же вели­чины именуют более выразительно - вероятности ложной тревоги и пропуска (сигнала), понимая под ложной трево­гой факт решения об обнаружении сигнала при условии, что он в наблюдаемом колебании у(t) не содержится, а под пропуском - объявление о том, что сигнала в y(t) нет при условии, что в действительности он в y(t) присутствует. Далее для вероятностей ложной тревоги и пропуска будут использованы обозначения p_лт=p₀₁ и Р_пс =Р₁₀. Средний риск при обнаружении , (2.4)

где П₀₁ и П₁₀ - риски, связан­ные с ложной тревогой и пропуском;

р₀ - априорная вероятность отсутствия s(t) в y(t).

Соотношения (2.2) и (2.3) в этом случае можно представить в виде:

, .

Помимо введенных общих критериев, не связанных с какими-либо допущениями относительно числа М прове­ряемых гипотез, при обнаружении часто применяют крите­рий Неймана - Пирсона, предписывающий добиваться ми­нимума вероятности пропуска Р_пс при ограничении сверху на вероятность ложной тревоги p_лт ≤ p_лт0. В нелинейном программировании известная теорема Куна-Таккера, согласно которой минимизация p_лт при p_лт≤p_лт0. равносильна безусловной минимизации целевой функции р_пс + μp_лт, где μ - неопределенный коэффициент Лагранжа. Положив p₀П₀₁ = μ (1-Р_о)П₁₀ и приведя (11) к виду

, (2.5)

нетрудно убедиться в возможности интер­претации и этого критерия как частного случая байесовского.