3.1.4. Предстационарная кинетика

Квазистационарное приближение всегда уменьшает число параметров, которые можно определить из эксперимента. Так, у нас есть три константы скорости k₁, k_1 и k₂ . Из значения w_max можно найти k₂. Но из величины K_M нельзя порознь найти k₁ и k_1. Однако исследование кинетики ферментативных реакций не только в стационарном, но и в предстационарном состоянии позволяет найти все константы.

C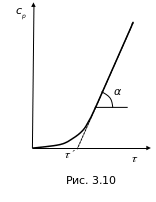 корость накопления продукта в предстационарном периоде изменяется, как показано на рис. 3.10. У этой зависимости есть два участка: нелинейный при малом времени и линейный, когда реакция уже вышла на стационарный режим. По этому линейному участку можно определить скорость процесса .

До того времени пока нельзя применить квазистационарное приближение, т.е. в предстационарный период кинетики, скорость накопления ферментсубстратного комплекса определяется уравнением

,

но согласно уравнению материального баланса , тогда получим

. (3.14)

Если концентрация фермента много меньше, чем концентрация субстрата, то концентрацию последнего можно считать постоянной. Это позволит проинтегрировать уравнение (3.14) после разделения переменных и получить следующее выражение

.

Скорость образования продукта выражается уравнением

,

или

. (3.15)

Если проинтегрировать выражение (3.15), получим зависимость концентрации продукта реакции от времени, т.е. уравнение кинетической кривой

.

Очевидно, что при больших значениях времени экспонента стремится к нулю и концентрация продукта от времени будет меняться линейно. Из последнего уравнения следует, что точка пересечения продолжения прямолинейной зависимости оси времени ( ) определяется выражением:

. (3.16)

Это время называется характеристическим временем.

С использованием этого понятия запишем выражение (3.15), причем выражение перед скобкой преобразуем следующим образом:

. (3.17)

Если время реакции и начальная концентрация субстрата много больше начальной концентрации фермента, т.е. постоянна, то уравнение (3.17) переходит в уравнение для квазистационарной концентрации фермент-субстратного комплекса, т.е. в уравнение вида

.

Удобно для дальнейшего анализа произвести следующие действия: умножить обе части (3.17) на . Тогда получим

. (3.18)

Величина в уравнении (3.18) есть начальная скорость ферментативной реакции в квазистационарном состоянии. Поскольку она постоянна, то интегрирование (3.18) приводит к

.

Когда реакция выходит на квазистационарный режим, концентрация продукта линейно зависит от времени ( ) .

.

Для нахождения констант скоростей отдельных стадий необходимо провести серию экспериментов, в которых предстационарная кинетика изучается в реакциях с различными начальными концентрациями субстрата. По каждой кинетической кривой определяется графически характеристическое время (экстраполяцией линейного участка кинетической кривой до пересечения с осью времени).

В результате получаем данные о значениях характеристического времени при разных значениях начальной концентрации субстрата.

Если преобразовать уравнение (3.16) к следующему виду:

,

то видно, что наклон прямой в координатах (рис. 3.11) будет равен , а отрезок, отсекаемый на оси ординат, дает сумму .

Д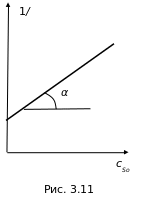 ля раздельного нахождения констант и нужно представить данные в двойных обратных координатах (координатах Лайнуивера-Берка), т.к. по уравнению Михаэлиса-Ментен

отрезок, отсекаемый на оси ординат, равен обратной величине максимальной (предельной) скорости, а она, в свою очередь, равна . Зная начальную концентрацию фермента, можно найти константу скорости , а потом вычислить .