Приклад № 2. Знайти графічним методом оптимальний розв’язок задачі, математична модель якої має вид:

цільова функція

;

обмеження:

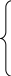
і .

Розв’язок:

Згідно з обмеженнями задачі, будуємо ОДР (рис. 5).

1. 

	0	6
	4	0

Множина точок, координати яких задовольняють нерівності , знаходиться нижче прямої , так як коефіцієнт біля змінної додатний (3>0), а знак нерівності “ ” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати менші, ніж відповідна точка на прямій .

2. 

	0	2
	2	0

Множина точок, координати яких задовольняють нерівності , знаходиться вище прямої , так як коефіцієнт біля змінної додатний (1>0), а знак нерівності “ ” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .

	0	-1
	1	0

Множина точок, координати яких задовольняють рівнянню знаходиться на прямій! Тому ОДР – це є відрізок АВ.

П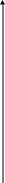 отім будуємо градієнт цільової функції - вектор з початком в точці та кінцем в точці (-3;1), а після цього – пряму цільової функції перпендикулярно до побудованого градієнта. Побудовану пряму переміщуємо за допомогою паралельного переносу вздовж градієнта і будуємо два образи: та між якими знаходиться відрізок АВ. Один з кінців відрізка відповідає мінімуму, а інший кінець – максимуму цільової функції. Так як за умовою задачі, необхідно знайти , то це значення знаходиться в точці А, яка утворюється прямими та . Розв’язуючи їх сумісно, знаходимо , а значення цільової функції .

Рис. 5.

Відповідь: . .

Приклад № 3. Знайти графічним методом оптимальний розв’язок задачі математична модель якої має вид:

цільова функція

;

обмеження:

і .

Розв’язок:

Згідно з обмеженнями задачі, будуємо ОДР (рис. 6).

1. .

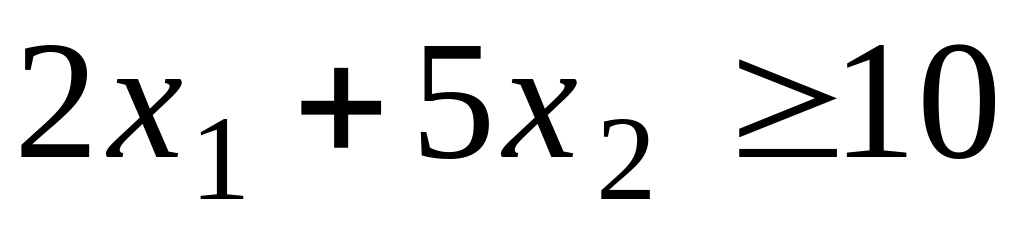	0	5
	2	0

Множина точок, координати яких задовольняють нерівності , знаходиться вище прямої , так як коефіцієнт біля змінної додатний (5>0), а знак нерівності “ ” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати більші, ніж відповідна точка на прямій .

2. .

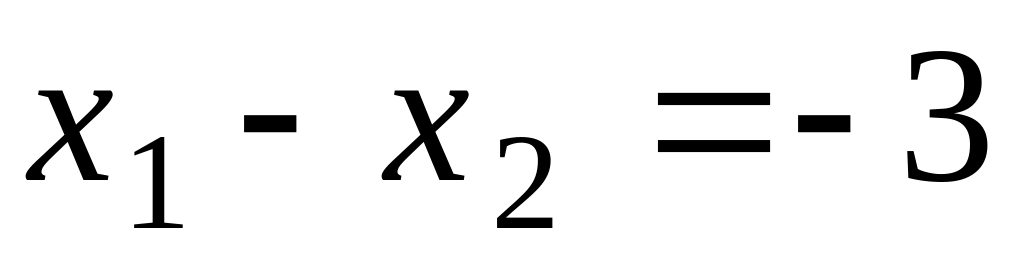	0	-3
	3	0

Множина точок, координати яких задовольняють нерівності , знаходиться нижче прямої , так як коефіцієнт біля змінної від’ємний (-1<0). Від’ємний коефіцієнт біля змінної вказує на те, що треба змінити напрямок розташування точок, які задовольняють нерівності, тобто знак нерівності “ ” вказує на те, що це мають бути точки, які при однакових значеннях абсцис мають ординати не більші, а менші, ніж відповідна точка прямої .

3. 

Ця пряма проходить паралельно вісі ординат через точку (4;0). Множина точок, яка задовольняє нерівності знаходиться зліва від прямої , тому що нерівність має знак “ ”.

Зверніть увагу на те, що математична модель має обмеження на змінні і , тобто область знаходиться тільки в першій координатній чверті. ОДР є чотирикутник АВСД.

Побудуємо тепер градієнт цільової функції з початком в точці та кінцем в точці (1;2,5). Після цього будуємо пряму цільової функції перпендикулярно до градієнта. Побудовану пряму переміщуємо за допомогою паралельного переносу вздовж градієнта і будуємо два образи: та між якими знаходиться побудована ОДР. Так як за умовою задачі, необхідно знайти , то це означає, що необхідно вказати точки мінімуму і максимуму, а також знайти відповідні значення цільових функцій та . З рисунку (6) видно, що образ , який відповідає мінімуму, співпадає з відрізком АД області, тобто дотиком є не кутова точка області, а цілий відрізок. Це означає, що задача має альтернативний мінімум, тобто точкою мінімуму є будь – яка точка відрізку АД. Знайдемо координати точок А і Д.

Точка А: А(0;2).

Точка Д: Д(4;0,4).

Координати будь – якої точки, що знаходиться на відрізку АД можуть бути знайдені за формулами:

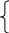тобто

де - довільне число.

Таким чином,

Так як образ гіперплощини дотикається ОДР в одній точці С, то значить цільова функція має один максимум.

Точка С: С(4;7).

Тому

Рис. 6.

Відповідь:

.