Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Sam_rabota.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

1.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Задача 2

Изучение распределения времени диагностирования. Для использования СМО необходимо, чтобы распределение времени обслуживания на посту диагностики подчинялось показательному закону. С целью исследования времени диагностирования В АТП проводилось хронометрование работ, выполняемых на постах диагностирования тормозной системы, рулевого управления и освещения. Полученные данные сведены в табл. 5.

Таблица 5

Время диагностирования

Номер разрядов	Границы разрядов в минутах	Опытные частоты
1	0-10	49
2	10-20	27
3	20-30	32
4	30-40	20
5	40-50	15
6	50-60	8
7	60-70	8
8	70-80	4
9	80-90	5
10	90-100	2
11	100-110	3
12	110-120	2

Н еобходимо проверить правдоподобность принятой статистической гипотезы путем проведения выравнивания полученных данных показательным законом.

Решение задачи 2

1. Строим гистограмму частот временя, расходуемого на диагностирование. Для этого по оси абсцисс откладываем середины интервалов, а по оси ординат соответствующие им частоты. Все вычисления сводим в табл. 6.

2. Вычисляем оценку математического ожидания по формуле (1):

1/175*(5*49+15*27+ …+115*2)=29,97

3. Определяем интенсивность процесса, т.е. среднее время, расходуемое на диагностирование

1/29,97=0,033

т.е. в минуту выполнялось 0,333 части работы, а в час 2 вида диагностирования.

4. Возможность выравнивания опытных данных показательным законом проверим по критерию Пирсона. Вычисляем вероятность попадания случайной величины в разряды и заносим в табл. 6.столбец 5.

P(0<t<10)=e^-^0,0330- e^-^0,03310=1-0,7189=0,281
P(10<t<20)=e^-^0,03310- e^-^0,03320=0,7189-0,5168=0,202

Таблица 6

Статистическая обработка экспериментальных данных задачи 2.

Номер разрядов	Границы разрядов	Середины разрядов	Опытные частоты	Теоретическая вероятность попадания в разряды	Теоретические частоты	Опыт
1	0-10	5	49	0,281	50	0,02
2	10-20	15	27	0,202	36	2,25
3	20-30	25	32	0,145	25	1,96
4	30-40	35	20	0,1045	18	0,22
5	40-50	45	15	0,1653	13	0,31
6	50-60	55	8	0,054	9	0,11
7	60-70	65	8	0,0388	7	0,14
8	70-80	75	4	0,0279	5	0,2
9	80-90	85	5	0,02	3	1,33
10	90-100	95	2	0,0144	2	0
11	100-110	105	3	0,0104	2	0,5
12	110-120	115	2	0,0074	1	1

Теоретические частоты вычислим по формуле:

и заносим в столбец 6 табл.6.

5. В столбике 7 табл.6 вычислены квадраты разностей опытных и теоретических частот, отнесенных к теоретическим частотам

χ²_набл=8,04,

По таблице приложения З по уровню значимости ά =0,05 и числу степеней свободы d=12-3=9 определяем

χ²_табл(ά=0,05; d=9)=16,9,
χ²_набл< χ²_табл

Следовательно, гипотеза о принадлежности экспериментальных данных к показательному закону по критерию согласия Пирсона оправдывается.

6. Строим выравнивающую кривую плотности показательного закона распределения. По оси абсцисс откладываем середины разрядов, п по оси ординат теоретические частоты. Гистограмма частот и выравнивающая кривая изображены на рис. 7.

Теоретическая кривая к задаче 2

ЗАДАЧА 3

Исследование соответствия давления воздуха в шинах, эксплуатируемых автомобилей, требованиям технических условий проводились в таксомотрном парке. Замеры давления воздуха осуществлялись при выезде автомобилей на линию, при этом использовался контрольный манометр, точность измерения которого ± 0,01. кг/см². Было проверено давления в 350 шинах, в результате получена следующая таблица отклонений давления воздуха от допустимого в кг/см².

Требуется выровнять полученные экспериментальные данные нормальным законом при допускаемом уровне значимости 0,01.

Таблица 7

Кол-во разрядов	Границы разрядов (отклонения давления воздуха)		Опытные частоты
1	-0,23	-0,21	3
2	-0,21	-0,19	8
3	-0,19	-0,17	19
4	-0,17	-0,15	37
5	-0,15	-0,13	53
6	-0,13	-0,11	60
7	-0,11	-0,09	64
8	-0,09	-0,07	49
9	-0,07	-0,05	31
10	-0,05	-0,03	17
11	-0,03	-0,01	7
12	-0,01	0	2

РЕШЕНИЕ ЗАДАЧИ III

1. Строим полигон относительных частот. Вычисляем относительные частоты и результаты заносим в табл. 8 столбец 4.

Р* = 3/350 = 0,009; Р₂* =8/350;

Определяем высоты прямоугольников, т.е. плотность относительной частоты и заносим результаты в столбец 6 табл. 8

Δх=0,02
Н₁=0,009/0,02=0,45 Н₂=0,023/0,02=1,15

Полигон относительных частот изображен на рис. 8.

2. Вычисляем опенку математического ожидания, дисперсии среднего квадратического отклонения по формулам (1), (2), (3), (4).

М*(х)= -0,1120; Д_В= - 0,0018;

S²=350/349*0.0018=0.0019 S= =0,045

3. Для определения теоретических частот рассчитываем

Значения функции φ(Ui) определяем по таблице приложения 1. Расчеты сведены в столбец 7, 8, 9 табл. 8.

4. Гипотезу о возможности выравнивания опытных данных нормальным законом проверяем по критерию согласия Пирсона, Вычисляем опытное значение критерия

=1,432

По таблице приложения 3 по уровню значимости ά =0,01 и числу степеней свободы d=12-3-9 определяем χ²_табл =21,7, χ²_набл< χ²_табл следовательно гипотезу о выравнивании опытных данных нормальным законом распределения принимаем.

5. Строим нормальную кривую. Для этого на перпендикулярах к серединам интервалов откладываем величину плотности теоретической вероятности, записанную в столбце 10 табл.8.Полученные точки соединяем кривой. Полигон относительных частот и выравнивающая теоретическая кривая изображены на рис. 8.

Рис. 8 Полигон относительных частот и выравнивающая кривая к задаче 3

Статистическая обработка экспериментальных данных задачи 3

Кол-во разрядов	Границы разрядов		Абсолютная частота	Относительная частота	Середины интервалов	Высоты прямоуг.		φ(U_i)		Плотность вероятности
1	-0,23	-0,21	3	0,009	-0,22	0,45	-2,4	0,0224	4	0,5
2	-0,21	-0,19	8	0,023	-0,2	1,15	-1,95	0,0596	9	1,32
3	-0,19	-0,17	19	0,054	-0,18	2,7	-1,51	0,1276	20	2,85
4	-0,17	-0,15	37	0,106	-0,16	5,3	-1,07	0,2251	35	5
5	-0,15	-0,13	53	0,151	-0,14	7,55	-0,62	0,3292	51	7,32
6	-0,13	-0,11	60	0,171	-0,12	8,55	-0,18	0,3925	61	8,7
7	-0,11	-0,09	64	0,183	-0,1	9,15	0,27	0,3847	60	8,55
8	-0,09	-0,07	49	0,14	-0,08	7	0,711	0,3101	49	6,9
9	-0,07	-0,05	31	0,088	-0,06	4,4	1,156	0,2036	32	4,5
10	-0,05	-0,03	17	0,049	-0,04	2,45	1,6	0,1109	18	2,45
11	-0,03	-0,01	7	0,02	-0,02	1	2,04	0,0498	8	1,1
12	-0,01	0	2	0,006	0	0,3	2,49	0,018	3	0,4

ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННОЙ ЗАВИСИМОСТИ,

ПОСТРОЕНИЕ ЛИНИИ РЕГРЕССИЙ

Если не удается опытные данные выровнять одним из вероятностных законов, то становится задача о построении аналитической зависимости между факторами. Наличие зависимости между факторами выявляется с помощью корреляционного анализа эмпирических данных. Вид конкретных зависимостей между переменными находятся с помощью регрессионного анализа, который решает проблему выбора соответствующего опытным точкам уравнения, наиболее точно отражающего природу изучаемого объекта.

Обычно экспериментальные точки дают некоторый разброс, т.е. обнаруживают случайные отклонения от видимой общей закономерности. Эти уклонения связаны с неизбежными при всяком опыте ошибками измерений. Разброс опытных точек называют корреляционным полем (рис.9).

Рис 9. Разброс опытных точек, отвечающих положительной корреляционной зависимости между результативным признаком у и факториальным признаком X, (а) - линия регрессии

В корреляционном поле одному значению факториального признака х соответствует несколько значений результативного признака y, поэтому строится зависимость

(26)

где - условное среднее, т.е. среднее арифметическое результативного признака у , соответствующих одному значению х.

Уравнение (26) называют уравнением регрессии.

Форма связи между переменными может выражаться любой аналитической функцией. Наиболее простой из них является линейная зависимость. Наличие линейной зависимости между у и х можно выявить с помощью коэффициента корреляции, определяемого равенством

(27)

где х_i, y_i - наблюдавшиеся значения признаков;

n_xy - частота пары значений (х_i, y_i);

n - сумма всех частот;

σ(x), σ(y) - средние квадратические отклонения, вычисляемые по формуле (2);

- выборочные средние, вычисляемые по формулам (1).

Чем ближе r_b, к единице, тем теснее линейная связь между переменными величинами. Если r_b близок к нулю, то это может свидетельствовать только об отсутствии линейной зависимости, а не зависимости вообще.

Величина коэффициента зависит от объема выборки. При одном и том же значении коэффициента корреляции, но при разном объеме выборки, исследуемые величины могут быть зависимы в одном случае и независимы в другом случае. Для статистической проверки значимости коэффициента корреляции можно воспользоваться рассчитанной Отделом статистики Института прикладной математики и механики г.Йена "Таблицей наибольших случайных значений коэффициента корреляции", помещенной в приложении 9. При заданном уровне значимости ά и числе степеней свободы d =k -2 по таблице, определяется наибольшее значение эмпирического коэффициента корреляции, при котором, исследуемые величины независимы. Если r_b расчетное больше определенного по таблице, то х и у связаны линейной зависимостью.

Установив наличие линейной связи, запишем уравнение прямой регрессии в виде:

(28)

В уравнении (28) каждому значению аргумента отвечает среднее значение функции. Нелинейные зависимости путем замены переменных в некоторых случаях можно свести к линейным. В табл.9 даны некоторые виды зависимостей и замена, приводящая их к линейным.

Исходная формула	Преобразованная формула	Формулы замены переменных	Окончательная формула	Примечание
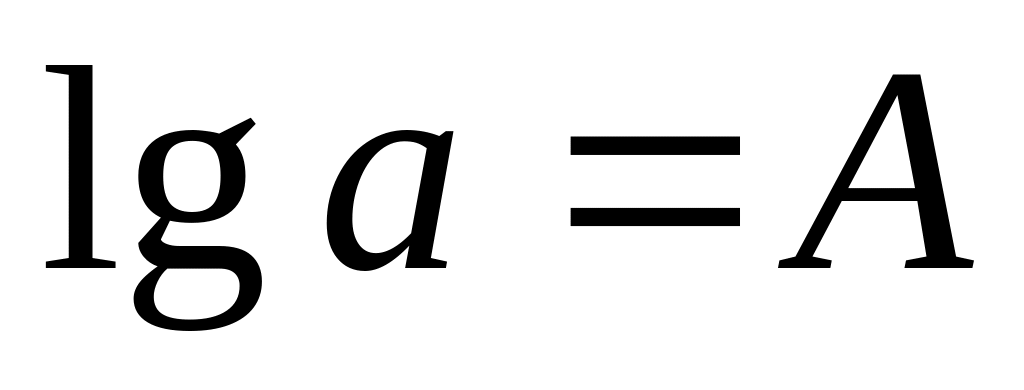
			Y=mX+A	Если m>0, кривая имеет вид параболы и проходит через начало координат Если m<0, кривая – гипербола, её асимптоты – координатные оси
			Y=Bx+A	Кривая проходит через точку (0;а).
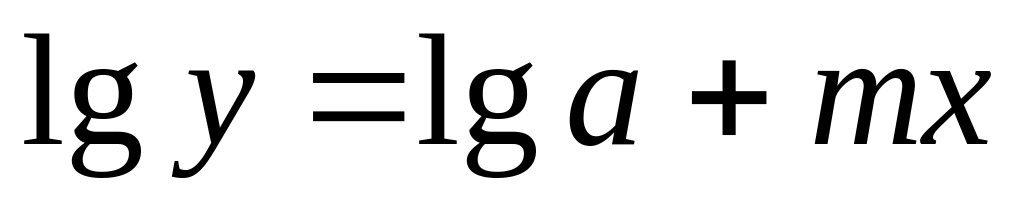
			Y=mx+A
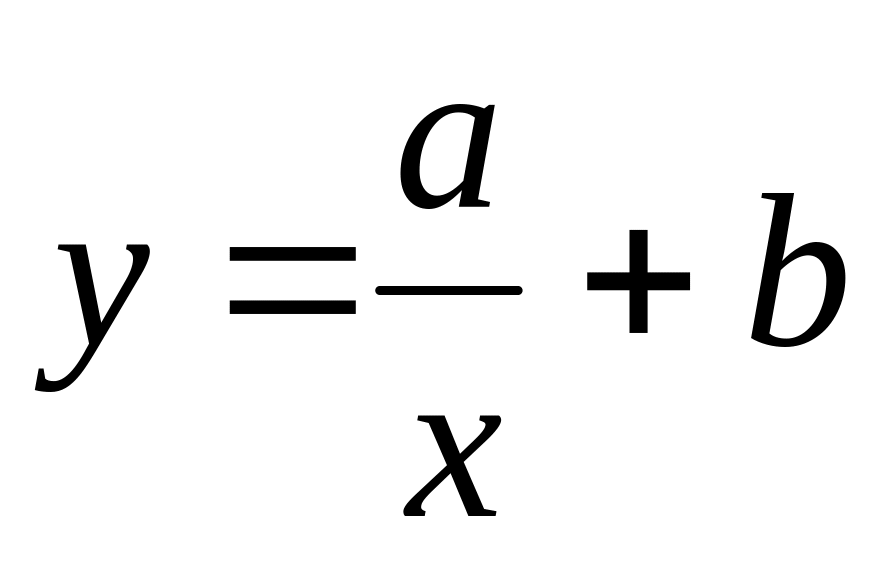
	-		Y=ax+b	Асимптоты кривой х=0, у=в
			Y=ax+b	Асимптоты кривой у=0, х=-в/а
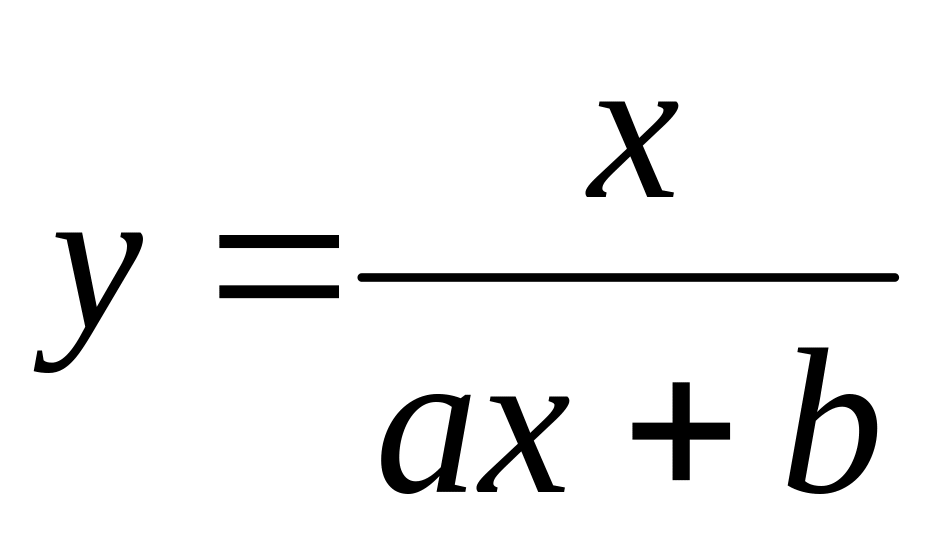
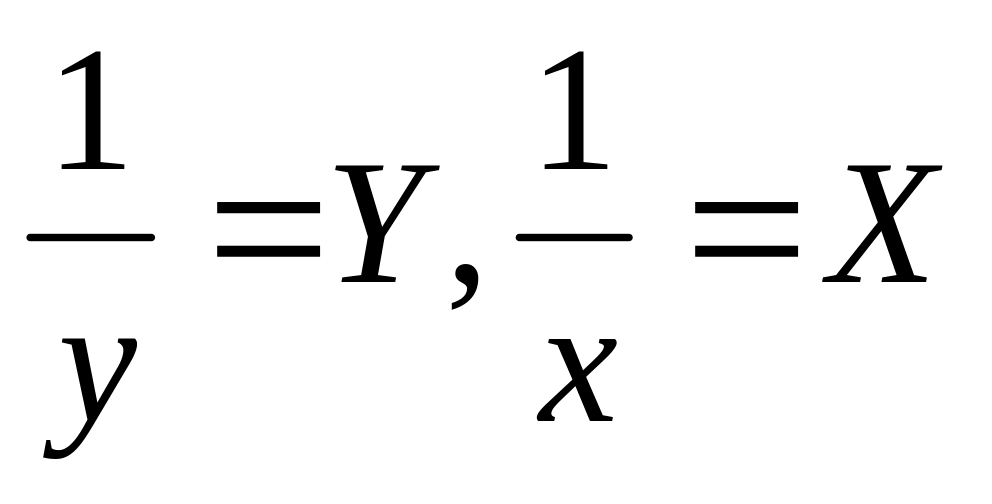
			Y=bx+a	Асимптоты кривой х=-в/а, у=1/а
	-	Lgx=X	Y=ax+b	Кривая проходит через точку (1;b)

Вид нелинейной зависимости можно подобрать по виду корреляционного поля, Но не всегда вид зависимости хорошо просматривается. Удобно вид эмпирической зависимости определить по простейшим необходимым условиям. Из опытных данных берем три точки: в начале, (x_S, y_S) в середине и (x₂, y₂) в конце корреляционного поля. Рассмотрим уравнение прямой у =кх + b. Пусть . Тогда соответствующее значение функции:

Таким образом, для любых двух точек прямой справедливо соотношение: среднему арифметическому значению аргумента соответствует среднее арифметическое значение функций.

Из выборки берем значение y_S соответствующее x_S и рассмотрим . Если это отклонение для какого-либо вида зависимости мало, то опытные данные можно выровнять (аппроксимировать) этой аналитической функцией. Аналогичные зависимости можно составить для различного вида функций (см. табл. 10).

Часто корреляционное поле является криволинейным и его можно описать кривой второго порядка, например, параболой

(29)

По опытным данным надо вычислить оценки коэффициентов а, b, с. Сделать это можно с помощью метода наименьших квадратов. Суть метода состоит в следующем: коэффициенты зависимости (29) вычисляются из условия, что сумма квадратов отклонений измеренных значений от расчетных принимает наименьшее значение.

Обозначим y_i - значение зависимостей переменной из опыта, - расчетное значение той же переменной. Составим сумму квадратов отклонений

(30)

Вместо подставим его значение из выражения ( 29 )

Получим функцию переменных а, b, с. Необходимым условием достижения минимума функцией Т(а, b, с ) есть равенство нулю частных производных

; ; .

Таблица 10

Простейшие необходимые условия для выбора эмпирических зависимостей

№ п/п	Вид эмпирической формулы
1	Y=ax+b	(среднее арифметическое)	(среднее арифметическое)
2	Y=ax^b	(среднее геометрическое)	(среднее геометрическое)
3	Y=ab^x	(среднее арифметическое)	(среднее геометрическое)
4	Y=a+b/x	(среднее гармоническое)	(среднее арифметическое)
5	Y=	(среднее арифметическое)	(среднее гармоническое)
6	Y=	(среднее гармоническое)	(среднее гармоническое)
7	Y=algx+b	(среднее геометрическое)	(среднее арифметическое)

Вычисляем производные и получаем систему нормальных уравнений

(31)

Суммы переменных х; у определяем из опытных данных. Систему (31) решаем матричным методом или методом Гаусса относительно неизвестных параметров а.,Ь,с.

Оценку тесноты нелинейной корреляционной связи определяют с помощью корреляционного отношения

(32)

где σ_межгр и σ_общ - соответственно межгрупповое и общее среднее квадратическое отклонение.

Межгрупповой дисперсией Д_межгр =σ²_межгр называют дисперсию групповых средних относительно общей средней

где - среднее значение переменной у , соответствующее одному значению Х;

- среднее значение всех замеров;

n_xi - частота значение х;

N - сумма всех частот;

Общей дисперсией Д_общ =r²_общ называют дисперсию значений признака всей совокупности относительно общей средней

где у_i - значение замера;

ny_i - частота значения у_i_.

Подставляя значения (r²_общ r²_межгр ) в формулу (32)_; получаем

В общем случае <=1, причем чем ближе корряляциониое отношение к единице, тем теснее связь между переменными. Если =0, то х и у корреляционной зависимостью не связаны. Корреляционное отношение служит мерой тесноты связи любой формы, в том числе и линейной.

Задача 4

С целью решения проблемы повышения надежности автомобилей проводится исследование зависимости коэффициента технической готовности (КТ) в АТП от чисел случаев ремонта. Статистическими наблюдениями было зафиксировано 96 результатов, сведенных в табл. 11.

Требуется исследовать тесноту связи между указанными параметрами и составить уравнение регрессии, описывающее зависимость КТГ от числа случаев ремонта

Решение. Данные 96 наблюдений сводим в корреляционную зависимость. Интервал изменения КТГ устанавливаем от его наименьшего значения 0,770 до наибольшего 0,980 и разбиваем его на шесть интервалов. Аналогично устанавливаем интервал изменения числа случаев ремонта, приходящиеся на 1000км пробега, от 0,00 до 1,80 и делим его на шесть равных интервалов. Определяем частоту совместного попадания переменных в интервалы. В результате получаем корреляционную таблицу, в которой обозначено через X - число случаев ремонта, приходящихся на 1000 км пробега, а через у - величина КТГ.

Таблица 11

Статистические данные наблюдения

№ п/п	Число случаев ремонта	КТГ	№ п/п	Число случаев ремонта	КТГ	№ п/п	Число случаев ремонта	КТГ
1	0,01	0,972	33	0,91	0,853	65	0,80	0,913
2	1,07	0,892	34	0,54	0,840	66	1,48	0,848
3	0,83	0,828	35	0,80	0,874	67	0,73	0,881
4	1,44	0,783	36	1,62	0,796	68	1,63	0,817
5	1,33	0,780	37	1,60	0,853	69	1,68	0,852
6	1,11	0,799	38	1,14	0,855	70	1,68	0,854
7	0,47	0,947	39	0,70	0,875	71	0,45	0,918
8	1,21	0,860	40	1,10	0,817	72	0,20	0,892
9	0,25	0,870	41	0,15	0,959	73	1,13	0,840
10	1	0,912	42	0,17	0,940	74	1,13	0,846
11	0,4	0,898	43	0,70	0,837	75	0,70	0,935
12	0,42	0,898	44	1,44	0,794	76	0,73	0,935
13	0,95	0,817	45	0,71	0,854	77	1,00	0,875
14	1,23	0,832	46	0,60	0,895	78	0,60	0,863
15	1,21	0,86	47	0,59	0,851	79	0,31	0,899
16	0,55	0,913	48	1,13	0,836	80	0,34	0,899
17	0,57	0,913	49	0,36	0,915	81	0,28	0,945
18	0,46	0,828	50	0,69	0,910	82	0,47	0,912
19	0,9	0,861	51	0,93	0,906	83	0,18	0,934
20	1,18	0,817	52	1,25	0,812	84	0,30	0,933
21	0,94	0,877	53	0,53	0,875	85	0,30	0,927
22	0,09	0,946	54	0,56	0,875	86	0,98	0,887
23	0,9	0,887	55	0,29	0,949	87	1,30	0,811
24	0,8	0,886	56	0,55	0,853	88	0,73	0,907
25	0,4	0,945	57	0,73	0,898	89	0,96	0,885
26	0,3	0,921	58	0,66	0,857	90	0,82	0,9
27	0,42	0,886	59	0,7	0,907	91	0,57	0,907
28	0,88	0,913	60	0,58	0,871	92	0,65	0,878
29	0,57	0,924	61	0,20	0,940	93	0,6	0,912
30	1,33	0,809	62	0,23	0,940	94	0,6	0,912
31	0,62	0,933	63	0,23	0,906	95	0,37	0,943
32	0,51	0,881	64	0,40	0,852	96	0,31	0,908

Таблица 12

Корреляционная таблица

	Х	0-0,3	0,3-0,6	0,6-0,9	0,9-1,2	1,2-1,5	1,5-1,8
у		0-0,3	0,3-0,6	0,6-0,9	0,9-1,2	1,2-1,5	1,5-1,8
0,77 0,805		4	1	-	-	-	-
0,805 0,84		9	11	6	1	-
0,84 0,875		2	7	9	6	-	-
0,875 0,91		1	5	7	5	3	3
0,91 0,945		-	-	2	4	4	1
0,945 0,98		-	-	-	1	3	1

Тесноту линейной связи между переменными устанавливаем с помощью выборочного коэффициента корреляции (27). Для проведения всех вычислений находим середины интервалов изменения переменных. Вычисления сводим в табл. 13.

=1/90(0,1516+0,4524 …+1,655)=0,7375
=1/96(0,78755+ … +0,9625*5)=0,8663
=1/96(0,7875²5+0,8225²*27+ …) =0,7523
=1-96(0,15²16+0,45²*24+ … )=0,7219
=0,4219
=0,0427

В корреляционной табл. 12 - в левом верхнем углу каждой клетки пишем произведение факторов, на пересечении которых стоит клетка. Полученное число умножаем на частоту, стоящую в клетке. Для контроля суммируем произведения по столбцам и рядам, в результате вычислений получаем

=62,5898.
=0,7301

Выборочный коэффициент корреляции довольно велик, это означает, что между рассматриваемыми признаками существует линейная корреляционная связь. Составляем уравнение прямой линии регрессии.

.
-0,8662=0,73010,0427/0,4219(х-0,7375)
=0,0739х+0,8117

_{Для
построения линии регрессии даем значения
переменной х и получаем значения
ух}

х=0,15 =0,823
х=1,65 =0,934

Построим эмпирическую кривую. Находим среднее значение переменной у, соответствующее одному значению переменной х.

х=0,15	=(0,78754+0,82259+0,85752+0,89251)/16=0,8225
х=0,45	=0,8458
х=0,75	=0,8648
х=1,05	=0,883
х=1,35	=0,9275
х=1,65	=0,9135

Обе кривые наносим на график рис. 11а.

Рис. 11а. Зависимость КТГ (ось ординат) от числа случаев ремонта (ось абсцисс): 1 - опытная, 2 – теоретическая выравнивающие линии регрессии опытного реляционного поля.

Таблица 13

Расчётная таблица к задаче 4

Середины интервалов		0,15	0,45	0,75	1,05	1,35	1,65	n_y	n_yy	n_yy²	n_yxyx
	Х	0-0,3	0,3-0,6	0,6-0,9	0,9-1,2	1,2-1,5	1,5-1,8	y
у		0-0,3	0,3-0,6	0,6-0,9	0,9-1,2	1,2-1,5	1,5-1,8	y
0,77 0,805		4	1	-	-	-	-	5	0,9375	3,1	0,8268
0,805 0,84		9	11	6	1	-		27	22,2075	18,2657	9,7467
0,84 0,875		2	7	9	6	-	-	24	20,58	17,6474	14,1481
0,875 0,91		1	5	7	5	3	3	24	24,42	19,1174	19,5457
0,91 0,945		-	-	2	4	4	1	11	10,2025	9,1174	11,8256
0,945 0,98		-	-	-	1	3	1	5	48,125	9,4628	6,4969
n_x		16	24	24	17	10	5	96	83,16	72,2254	62,5898
n_xx		2,4	10,8	18	17,85	13,5	8,25	70,8
n_xx²		0,36	4,86	13,5	18,7425	18,225	13,6125	69,3
n_xyxy		1,9741	9,1341	15,5663	15,8576	12,5213	7,5363	62,5898

Приложение 1

Таблица значений функции

Приложение 2

Таблица значений функции

x	φ(x)	x	φ(x)	x	φ(x)	x	φ(x)	x	φ(x)
0	0	0,57	0,2157	1,14	0,3729	1,71	0,4564	2,56	0,4948
0,01	0,0040	0,58	0,2190	1,15	0,3749	1,72	0,4573	2,58	0,4951
0,02	0,0080	0,59	0,2224	1,16	0,3770	1,73	0,4582	2,60	0,4953
0,03	0,0120	0,60	0,2257	1,17	0,3790	1,74	0,4591	2,62	0,4956
0.04	0,0160	0,61	0,2291	1,18	0,3810	1,75	0,4599	2,64	0,4959
0,05	0,0199	0,62	0,2324	1,19	0,3830	1,76	0,4608	2,66	0,4961
0.06	0,0239	0,63	0,2357	1,20	0,3849	1,77	0,4616	2,68	0,4963
0,07	0,0279	0,64	0,2389	1,21	0,3869	1,78	0,4625	2,70	0,4965
0,08	0,0319	0,65	0,2422	1,22	6,3883 ]	1,79	0,4633	2,72	0,4967
0,09	0,0359	0,66	0,2454	1,23	0,3907	1,80	0,4641	2,74	0,4969
0,10	0,0398	0,67	0,2486	1,24	0,3925	1,81	0,4649	2,76	0,4971
0,11	0,0438	0,68	0,2517	1,25	0,3944	1,82	0,4656	2,78	0,4973
0.12	0,0478	0,69	0,2549	1,26	0,3962	1,83	0,4664	2,80	0,4974
0,13	0,0517	0,70	0,2580	1,27	0,3980	1,84	0,4671	2,82	0,4976
0.14	0,0357	0,71	0,261	1,28	0,3997	1,85	0,4678	2,84	0,4977
0,15	0,0596	0,72	0,2642	1.29	0,4015	1,86	0,4686	2,86	0,4979
0,16	0,0636	0,73	0,2673	1,30	0,4032	1,87	0,4693	2,88	0,4980
0,17	0,0675	0,74	0,2703	1,31	0,4049	1,88	0,4699	2,90	0,4981
0,18	0,0714	0,75	0,2734	1,32	0,4066	1,89	0,4706	2,92	0,4982
0,19	0,0753	0,76	0,2764	1,33	0,4082	1,90	0,4713	2,94	0,4984
0,20	0,0793	0,77	0,2794	1,34	0,4099	1,91	0,4719	2,96	0,4985
0,21	0,0832	0,78	0,2823	1,35	0,4115	1,92	0,4726	2,98	0,4986
0,22	0,0871	0,79	0,2852	1,36	0,4131	1,93	0,4732	3,00	0,49865
0,23	0,0910	0,80	0,2881	1.37	0,4147	1,94	0;4738	3,20	0,49931
0,24	0,0948	0,81	0,2910	1,38	0,4162	1,95	0,4744	3,40	0,49966
0,25	0,0987	0,82	0,2939	1.39	0,4177	1,96	0,4750	3,60	0,49984
0,26	0,1026	0,83	0,2967	1,40	0,4192	1,97	0,4756	3,80	0,49992
0,27	0,1064	0,84	0,2995	1.41	0,4207	1,98	0,4761	4,00	0,49996
0,28	0,1103	0,85	0,3023	1.42	0,4222	1,99	0,4767	4,50	0,49999
0,29	0,1141	0,86	0,3051	1,43	0,4236	2,00	0,4772	5,00	0,49999
0,3	0,1179	0,87	0,3078	1,44	0,4251	2,02	0,4783
0,31	0,1217	0,88	0,3106	1.45	0,4265	2,04	0,4793
0,32	0,1255	0,89	0,3133	1,46	0,4279	2,06	0,4803
0,33	0,1293	0,90	0,3159	1.47	0,4292	2,08	0,4812
0,34	0,1331	0,91	0,3186	1,48	0,4306	2,10	0,4821
0,35	0,1368	0,92	0,3212	1,49	0,4319	2,12	0,4830
0,36	0,1406	0,93	0,3238	1.50	0,4332	2,14	0,4838
0,37	0,1443	0,94	0,3264	1.51	0,4345	2,16	0,4846
0,38	0,1480	0,95	0,3289	1.52	0,4357	2,18	0,4854
0,39	0,1517	0,96	0,3315	1.53	0,4370	2,20	0,4861
0,40	0,1554	0,97	0,3340	1,54	0,4382	2,22	0,4868
0,41	0,1591	0,98	0,3365	1.55	0,4394	2,24	0,4875
0,42	0,1628	0,99	0,3389	1,56	0,4406	2,26	0,4881
0,43	0,1664	1,00	0,3414	1,57	0,4418	2,28	0,4887
0,44	0,1700	1,01	0,3438	1,58	0,4429	2,30	0,4893
0,45	0,1736	1,02	0,3461	1,59	0,4441	2,32	0,4898
0,46	0,1772	1,03	0,3485	1,60	0,4452	2,34	0,4904
0,47	0,1003	1,04	0,3508	1,61	0,4463	2,36	0,4909
0,48	0,1644	1,05	0,3531	1,62	0,4474	2,38	0,4913
0,49	0,1879	1.06	0,3554	1,63	0,4484	2,40	0,4918
0,50	0,1915	1,07	0,3577	1,64	0,4495	2,42	0,4922
0,51	0,1950	1,08	0,3599	1,65	0,4505	2,44	0,4927
0,52	0,1985	1,09	0,3621	1,66	0,4515	2,46	0,4931
0,53	0,2019	1,10	0,3643	1,67	0,4525	2,48	0,4934
0,54	0,2054	1,11	0,3665	1,68	0,4535	2,50	0,4938
0,55	0,2088	1,12	0,3686	1,69	0,4545	2,52	0,4941
0,56	0,2123	1,13	0,3708	1,70	0,4554	2,54	0,4945

Приложение 3

^{Критические
точки распределения χ}2

Число степеней свободы к	Уровень значимости ά
Число степеней свободы к	0,01	0,025	0,05	0,95	0,975	0,99
1	6,6	5,0	3,8	0,0039	0,00098	0,00016
2	9,2	7,4	6,0	0,103	0,051	0,020
3	11,3	9,4	7,8	0,352	0.216	0,115
4	13,3	11,1	9,5	0,711	0,484	0,297
5	15,1	12,8	11,1	1,15	0,831	0,554
6	16,8	14,4	12,6	1,64	1,24	0,872
7	18,5	16,0	14,1	2,17	1,69	1,24
8	20,1	17,5	15,5	2,73	2,18	1,65
9	21,7	19,0	16,9	3,33	2,70	2,09
10	23,2	20,5	18,3	3,94	3,25	2,56
11	24,7	21,9	19,7	4,57	3,82	3,05
12	26,2	23,3	21,0	5,23	4,40	3,57
13	27,7	24,7	22,4	5,89	5,01	4,11
14	29,1	26,1	23,7	6,57	5,63	4,66
15	30,6	27,5	25,0	7,26	6,26	5,23
16	32,0	28,8	26,3	7,96	6,91	5,81
17	33,4	30,2	27,6	8,67	7,56	6,41
18	34,8	31,5	28,9	9,39	8,23	7,01
19	36,2	32,9	30,1	10,1	8,91	7,63
20	37,6	34,2	31,4	10,9	9,59	8,26
21	38,9	35,5	32,7	11,6	10,3	8,90
22	40,3	36,8	33,9	12,3	11,0	9,54
23	41,6	38,1	35,2	13,1	11,7	10,2
24	43,0	39,4	36,4	13,8	12,4	10,9
25	44,3	40,6	37,7	14,6	13,1	11,5
26	45,6	41,9	38,9	15,4	13,8	12,2
27	47,0	43,2	40,1	16,2	14,6	12,9
28	48,3	44,5	41,3	16,9	15,3	13,6
29	49,6	45,7	42,6	17,7	16,0	14,3
30	50,9	47,0	43,8	18,5	16,8	15

Приложение 4

^{Значения
ех и е-х}

е^х	х	е^-х
1,0010	0,001	0,9990
1,0020	0,002	0,9980
1,0030	0,063	0,9970
1,0040	0,004	0,9960
1,0050	0,005	0,9950
1,0060	0,006	0,9940
1,0070	0,007	0,9930
1,0080	0,008	0,9920
1,0090	0,009	0,9910
1,0100	0,01	0,9900
1,0202	0,02	0,9801
1,0304	0,03	0,9704
1,0408	0,04	0,9607
1,052	0,05	0,9512
1,0610	0,06	0,9417
1,0725	0,07	0,9323
1,0832	0,08	0,9231
1,0941	0,09	0,9139
1,1051	0,1	0,9048
1,2214	0,2	0,8187
1,3498	0,3	0,7408
1,4918	0,4	0,6703
1,6487	0,5	0,6065
1,8221	0,6	0,5488
2,0137	0,7	0,4965
2,2255	0,8	0,4493
2,4596	0,9	0,4065
2,7182	1	0,3678
7,3890	2	0,1353
20,0855	3	0,4978*10^-1
54,5981	4	0,1831*10^-1
148,4131	5	0,6737*10^-2
403,4287	6	0,2478*10^-2
11096,6331	7	0,9118*10^-3
2980,9579	8	0,3354*10^-3
8103,084	9	0,000123
22026,47	10	4,54E-05
59874,14	11	1,67E-05
162754,8	12	6,14E-06
442413,4	13	2,26E-06
1202604	14	8,32E-07
3269017	15	3,06E-07
8886111	16	1,13E-07
24154953	17	4,14E-08
65659969	18	1,52E-08
1,78E+08	19	5,6E-09
4,85E+08	20	2,06E-09
1,32E+09	21	7,58E-10
3,58E+09	22	2,79E-10
9,74E+09	23	1,03E-10
2,65E+10	24	3,78E-11
7,2E+10	25	1,39E-11
1,96E+11	26	5,11E-12
5,32E+11	27	1,88E-12
1,45E+12	28	6,91E-13
3,93E+12	29	2,54E-13
1,07Е+13	30	9,36E-14

Приложение 5

^{Зависимость
между коэффициентом вариации и параметром
формы закона Вейбулла}

	n
15,83	0,2	120	190,0
5,29	0,3	8,86	46,9
3,14	0,4	3,32	10,4
2,24	0,5	2,00	4,47
1,74	0,6	1,50	2,61
1,46	0,7	1,27	1,86
1,26	0,8	1,13	1,43
1,11	0,9	1,05	1,17
1,00	1	1,0	1.0
0,910	1,1	0,965	0,878
0,837	1,2	0,941	0,787
0,775	1,3	0,924	0,716
0,723	1,4	0,911	0,659
0,678	1,5	0,903	0,612
0,640	1,6	0,897	0,574
0,605	1.7	0,892	0,540
0,575	1,8	0,889	0,512
0,547	1,9	0,887	0,485
0,523	2,0	0,886	0,463
0,498	2,1	0,886	0,441
0,480	2,2	0,886	0,425
0,461	2,3	0*886	0,409
0,444	2,4	0,887	0,394
0,428	2,5	0,887	0,380
0,365	3,0	0,893	0,326
0,315	3,5	0,900	0,285
0,281	4,0	0,906	0,255

Приложение 6

Плотности вероятностей закона Вейбулла в зависимости от параметра формы n и параметра масштаба а, умноженные на параметр а:

	n	0,4	0,6	0,8	1	1,2	1,4	1,6	1,8	2
a		0,4	0,6	0,8	1	1,2	1,4	1,6	1,8	2
0,1		1,06	1,17	1,08	0,90	0,71	0,53	0,39	0,28	0,19
0,2		0,62	0,78	0,83	0,81	0,75	0,66	0,56	0,47	0,33
0,3		0,44	0,59	0,69	0,74	0,74	0,72	0,67	0,61	0,55
0,4		0,34	0,48	0,59	0,67	0,71	0,73	0,73	0,71	0,68
0,5		0,28	0,40	0,51	0,60	0,67	0,73	0,76	0,78	0,78
0,6		0,24	0,35	0,46	0,55	0,63	0,67	0,75	0,80	0,83
0,7		0,21	0,31	0,40	0,50	0,58	0,66	0,73	0,79	0,85
0,8		0,18	0,27	0,36	0,45	0,53	0,61	0,69	0,77	0,84
0,9		0,16	0,25	0,33	0,40	0,49	0,56	0,64	0,72	0,80
1,0		0,15	0,22	0,29	0,37	0,44	0,51	0,58	0,66	0,73
1,1		0,13	0,20	0,27	0,33	0,40.	0,47	0,53	0,59	0,65
1,2		0,12	0,18	0,24	0,30	0,36	0,41	0,47	0,52	0,59
1,3		0,11	0,17	0,22	0,27	0,32	0,37	0,41	0,45	0,48
1,4		0,10	0,15	0,20	0,27	0,29	0,33	0,35	0,38	0,39
1.5		0,10	0,14	0,18	0,22	0,26	0,28	0,30	0,31	0,32
1,6		0,09	0,13	0,17	0,20	0,23	0,24	0,25	0,25	0,25
1,7		0,08	0,13	0,16	0,18	0,20	0,21	0,21	0,20	0,19
1,8		0,08	0,11	0,14	0,16	0,18	0,18	0,17	0,16	0,14
1,9		0,07	0,10	0,13	0,15	0,16	0,15	0,14	0,13	0,10
2,0		0,07	0,10	0,12	0,13	0,14	0,15	0,12	0,09	0,07
2,1		0,07	0,09	0,11	0,12	0,12	0,11	0,09	0,07	0,05
2,2		0,06	0,09	0,10	0,11	0,11	0,09	0,07	0,05	0,03
2,3		0,06	0,08	0,10	0,10	0,09	0,08	0,06	0,04	0,02
2,4		0,05	0,08	0,09	0,09	0,08	0,07	0,05	0,03	0,01
2,5		0,05	0,07	0,08	0,08	0,07	0,05	0,03	0,02	0,00

Приложение 7

Вероятности исправной работы изделия, распределенные по закону Вейбулла в зависимости от параметра формы n и параметра масштаба μ:

	n	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1	1,2	1,3	1,4	1,5
1/a		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1	1,1	1,2	1,3	1,4	1,5
0,1		45	53	66	73	78	82	85	88	90	92	94	95	96	97	97
0,2		43	48	54	64	68	72	76	79	82	84	86	88	90	91	93
0,3		41	46	49	58	62	65	68	71	74	76	79	от	83	85	86
0,4		40	43	47	53	56	59	61	64	67	69	71	74	76	77	79
0,5		39	42	44	49	52	54	56	58	60	63	64	67	68	70	72
0,6		39	40	42	46	48	49	51	53	54	56	58	59	61	63	64
0,7		38	39	40	53	44	49	47	49	49	51	52	53	54	56	57
0,8		37	38	39	41	42	42	43	44	45	46	46	47	48	49	49
0,9		37	37	38	38	39	39	39	40	40	41	41	42	42	42	43
1,0		37	37	37	37	37	37	37	37	37	37	37	37	37	37	37
1,1		36	36	36	35	35	34	34	34	33	33	33	32	32	31	31
1,2		36	35	35	33	33	32	31	30	30	29	29	28	27	27	26
1,3		34	35	од	32	31	30	29	28	27	26	25	24	24	23	22
1,4		35	34	33	30	29	28	27	26	25	23	23	21	20	19	18
1.5		35	34	33	29	28	26	25	24	22	21	20	18	17	16	15
1,6		35	33	31	28	26	25	23	22	20	19	17	16	14	13	12
1,7		35	33	31	27	26	23	22	20	18	17	15	14	12	10	09
1,8		34	33	30	26	24	22	20	18	16	15	13	11	10	08	07
1,9		34	32	29	25	23	21	19	17	15	13	11	09	08	07	06
2,0		34	32	29	24	22	20	17	15	13	11	10	08	07	06	05

Все значения Р_испр меньше единицы, поэтому в таблице приведены лишь десятичные знаки, стоящие после запятой, перед которой при пользовании таблицей нужно ставить нуль.

Приложение 8

Наибольшие случайные значения коэффициента корреляции

Число степеней свободы d	Уровень значимости ά
Число степеней свободы d	0,05	0,01	0,0027	0,001
5	0,75	0,87	0,93	0,95
10	0,58	0,71	0,78	0,82
15	0,48	0,61	0,68	0,72
20	0,42	0,53	0,61	0,65
25	0,38	0,49	0,55	0,60
30	0,35	0,45	0,51	0,55
35	0,32	0,42	0,48	0,52
40	0,30	0,39	0,45	0,49
50	0,27	0,35	0,41	0,44
60	0,25	0,33	0,37	0,41
70	0,23	0,30	0,35	0,38
80	0,22	0,28	0,33	0,36
90	0,21	0,26	0,31	0,34
100	0,19	0,25	0,29	0,32
120	0,18	0,23	0,27	0,30
150	0,16	0,21	0,24	0,26
200	0,14	0,18	0,21	0,23
300	0,11	0,15	0,17	0,19
400	0,10	0,13	0,15	0,16
500	0,09	0,11	0,13	0,15
700	0,07	0,10	0,11	0,12
900	0,06	0,09	0,10	0,11
1000
и более	0,06	0,09	0,10	0,11

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

Кафедра «Автомобили и автомобильное хозяйство»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению самостоятельных работ по дисциплине

«Техническая эксплуатация автомобилей»

(для студентов квалификационного уровня

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.12.2018688.13 Кб5RU_Тезисы лекций прокурорский надзор в Украине.doc
#
01.07.2025240.97 Кб0ruДиплом Гнип русский.docx
#
03.11.2018838.66 Кб5RYe_2008_ukr_nov_dlya_izd.doc
#
31.08.201979.36 Кб1Samomenedzhment.doc
#
15.11.2018107.01 Кб3samrab_1TP.doc
#
01.07.20251.42 Mб0Sam_rabota.doc
#
01.07.2025326.14 Кб0Schodennik_z_virobnichoyiyi_praktiki_sestr_spra...doc
#
01.03.202582.26 Кб0Schpora.docx
#
18.11.2019411.65 Кб10Section 7 Milk and milk goods.doc
#
26.04.20191.45 Mб6sekin.doc
#
12.11.2019183.81 Кб5seminari_4.doc

=1/90(0,1516+0,4524 …+1,655)=0,7375
=1/96(0,78755+ … +0,9625*5)=0,8663
=1/96(0,7875²5+0,8225²*27+ …) =0,7523
=1-96(0,15²16+0,45²*24+ … )=0,7219
=0,4219
=0,0427