9.3. Метод непосредственного интегрирования при определении перемещений в балках. Граничные условия

Остановимся на применении уравнения (9.4) при определении прогибов и углов поворота сечений балки методом непосредственного интегрирования. Это уравнение есть дифференциальное уравнение второго порядка с разделенными переменными. Поэтому его интегрирование выполняется по довольно простой схеме. Первый интеграл позволяет найти углы поворота φ(z), т.е.:

; (а)

Вторичное интегрирование дает возможность найти функцию прогиба v(z):

(б)

Формулы (а) и (б) содержат две произвольные постоянные интегрирования С₁ и С_2., которые можно найти из граничных условий для функций прогиба и угла поворота в балке, вытекающих из условия закрепления балки идеальными связями.

Н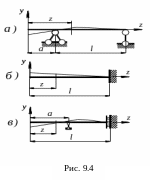 а рис. 9.4 показаны наиболее часто встречающиеся способы закрепления и связанные с ними граничные условия.

Для балки на рис. (9.4, а) имеем:

при

z=a, прогиб v=0;

при

z=l+a, прогиб v=0.

Для балки на рис. (9.4, б)

при

z=l, прогиб v=0;

угол поворота φ=0

Для балки на рис. (9.4, в)

при z=a, прогиб v=0;

при z=l, угол поворота φ=0

Таким образом, для каждой представленной балки имеется по два граничных условия. Это позволяет определять постоянные интегрирования С₁ и С₂ в решениях (а) и (б).

Проследим применение метода непосредственного интегрирования для определения перемещений в конкретном случае.

П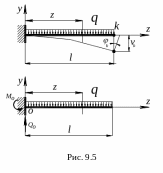 ример № 9.1.

Определить прогиб свободного конца балки с изгибной жесткостью EJ_x (рис. 9.5) методом непосредственного интегрирования дифференциального уравнения изогнутой оси балки.

Решение.

Решение основано на использовании дифференциального уравнения (9.4).

Опорные реакции М₀=ql/2, Q₀=ql. Изгибающий момент в текущем сечении:

М(z) = -М₀+Q₀ z-qz²/2=-ql²/2+qlz-qz²/2

Подставим М(z) в уравнение (9.4) получим:

Проинтегрируем первый раз:

Второе интегрирование дает:

Граничные условия: при z=0, v=0, φ=0. С их учетом получаем С₁= С₂=0. Прогиб свободного конца при z=l получаем:

Знак минус у прогиба v_k показывает, что его направление противоположно положительному направлению оси у, а знак минус у угла поворота φ_к указывает на поворот сечения свободного конца балки по ходу часовой стрелки.

Пример № 9.2.

О пределить прогиб v_k в середине пролета балки постоянной жесткости EJ_x и углы поворота φ_А и φ_В опорных сечений (рис. 9.6) методом непосредственного интегрирования дифференциального уравнения (9.4).

Решение.

Ответы на поставленные вопросы дадим, используя уравнение (9.4). Изгибающий момент в сечении левого участка М^I(z)=Аz=Рz/2, а в сечении правого участка изибающий момент M^II(z)=Р(l-z)/2. Тогда дифференциальные уравнения на каждом участке балки будут иметь вид:

(а)

(б)

Интегрируем дважды сначала уравнение (а), а потом уравнение (б) получаем:

Граничные условия: при z=0, v^I=0; при z=l, v^II=0. Из второго уравнения следует, что D₁=0. Четвертое уравнение дает соотношение:

, или

Воспользуемся условием симметрии балки и нагрузки. При z=l/2, φ^I=0. Тогда . Из условия симметрии балки при z=l/2, φ^I=φ^II получим: . Тогда значение постоянной интегрирования . Подставим значения постоянных интегрирования, получим уравнения углов поворота и прогибов на каждом участке балки в виде:

(в)

(г)

(д)

(е)

Определим углы поворота сечений балки над опорами А и В. Используя уравнение (в) при z=0, получаем . По уравнению (д) при z=l находим . Прогиб в середине пролета балки можно получить из уравнения (г), либо из уравнения (е) при z=l/2. Его значение составит:

_{Приведенные примеры показывают, что применение метода непосредственного интегрирования ограничено на практике. Это связано с тем что при определении постоянных интегрировании приходится решать систему 2n линейных алгебраических уравнений. На практике более широкое применение находят другие методы, основанные на использовании уравнения (9.4).}