2.9.1 Влияние неравномерности распределения скоростей u по плоскому живому сечению на количество движения (кд) массы м.

Действительное количество движения массы dM:

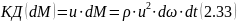
Действительное количество движения массы M:

«Среднее» количество движения массы М:

Существенно подчеркнуть, что

КД (М) > [КД(М)]_ср (2.36)

Разделим (2.34) на (2.35):

где α₀ – корректив количества движения потока (коэффициент Буссинеска);

Пользуясь введённым обозначением α₀, можем написать:

Действительная величина количества движения массы жидкости М, проходящей за время dt через рассматриваемое живое сечение равна средней величине количества движения (подсчитанной в предположении, что все частцы жидкости проходят данное живое сечение с одинаковой скоростью ), умноженной на некоторый безразмерный поправочный коэффициент α₀.

2.9.2. Влияние неравномерности распределения скоростей u по плоскому живому сечению на кинетическую энергию (кэ) массы м.

Действительная кинетическая энергия массы dM:

Действительная кинетическая энергия всей массы М:

Средняя кинетическая энергия массы М:

Подчеркнём, что

КЭ (М) > [КЭ(М)]_ср (2.43)

Разделим (2.41) на (2.42)

где α – корректив кинетической энергии (коэффициент Кориолиса).

При равномерном движении жидкости и турбулентном режиме α₀ и α, установленные на основании опытов, часто оказываются равными: ; .

2.10 Уравнение Бернулли для целого потока реальной (вязкой) жидкости при установившемся движении.

Уравнение Бернулли представляет собой гидравлическое выражение закона сохранения и превращения энергии.

Для потока реальной (вязкой) несжимаемой жидкости оно имеет вид

Здесь z – высота расположения рассматриваемой точки в потоке жидкости над некоторой горизонтальной плоскостью О-О, называемой плоскостью сравнения; р – гидродинамическое давление в рассматриваемой точке; γ – вес единицы объёма жидкости; α – корректив кинетической энергии, учитывающий неравномерность распределения скоростей в рассматриваемом живом сечении потока; – средняя скорость движения жидкости в рассматриваемом живом сечении; g – ускорение свободного падения.

Рис. 2.15 Геометрическая интерпретация уравнения Бернулли

z – геометрическая (геодезическая) высота;

- пьезометрическая высота;

- скоростная высота.

Энергетический смысл уравнения Бернулли заключается в том, что левая его часть является выражением полной удельной энергии жидкости. Это полная энергия единицы веса жидкости в живом сечении 1-1 потока. В правой части аналогичное выражение для живого сечения 2-2, расположенного ниже по течению от сечения 1-1.

В гидравлике полная удельная энергия жидкости, отнесённая к единице веса называется напором и обозначается Н. Поэтому уравнение Бернулли можно записать упрощённо:

В соответствии с законом сохранения и превращения энергии , так как при движении жидкости в ней возникают касательные напряжения трения, на преодоление которых и затрачивается часть полной удельной энергии потока.

h_w – полная удельная энергия, теряемая в среднем единицей веса жидкости на пути от первого до второго сечения за счёт внешних и внутренних сил трения.

Энергетический смысл других членов уравнения Бернулли:

z – удельная потенциальная энергия положения;

– удельная потенциальная энергия давления;

z+ - полная удельная потенциальная энергия (потенциальный напор);

– удельная кинетическая энергия (скоростной напор).

Все члены уравнения Бернулли измеряются в единицах длины столба той жидкости, для которой вычисляется напор.

Если между сечениями 1-1 и 2-2 установить пьезометры и соединить уровни жидкости в них линией, то получим так называемую пьезометрическую линию Р-Р. Выше пьезометрической линии Р-Р располагается напорная линия Н-Н. В любом живом сечении вертикальное расстояние между линиями Р-Р и Н-Н равно скоростной высоте в этом сечении.

Элементарное снижение напорной линии , отнесённое к соответствующей элементарной длине ds, отмеренной по оси потока, называется гидравлическим уклоном и обозначается через i.

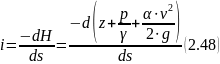
Соответственно элементарное снижение (повышение) пьезометрической линии, отнесённое к соответствующей элементарной длине ds, отмеренной по оси потока, называется пьезометрическим уклоном и обозначается через I.

Гидравлический и пьезометрический уклоны считаются положительными, если напорная и пьезометрическая линии вдоль потока по течению снижаются. Поскольку напор постоянно уменьшается вниз по течению и напорная линия всегда понижается в этом направлении (вследствие потери потоком энергии на преодоление внутренних и внешних сил трения), то гидравлический уклон всегда положителен.

Пьезометрическая линия на отдельных участках может повышаться за счет перехода удельной кинетической энергии в потенциальную энергию. В этом случае на данном участке пьезометрический уклон будет отрицательным.

Рисунок 2.15 даёт нам полную гидродинамическую картину:

а) фигура, заключённая между линией Р-Р и осью потока, представляет собой эпюру изменения величины (пьезометрической высоты) вдоль потока;

б) фигура, заключённая между линиями Р-Р и Н-Н, даёт эпюру изменения скоростного напора ; следовательно, эта фигура выражает и характер изменения скорости вдоль потока;

в) фигура, заключённая между линией Н-Н и плоскостью сравнения О-О, представляет собой эпюру изменения полного напора вдоль потока.

Условия применимости уравнения Бернулли.

1. Расход Q между сечениями 1-1 и 2-2 должен быть постоянен.

2. Движение жидкости должно быть установившимся, поскольку при выводе уравнения считали, что кинетическая энергия жидкости, заключённая в объёме между сечениями 1-1 и 2-2, не изменяется во времени.

3. Движение жидкости в сечениях 1-1 и 2-2, соединяемых уравнением Бернулли, должно быть параллельноструйным или плавно изменяющимся; в промежутках же между сечениями 1-1 и 2-2 движение жидкости может быть и резко изменяющимся.

Обстоятельства движения потока между сечениями 1-1 и 2-2 непосредственно учитываются в уравнении Бернулли только членом h_w. Если мы имеем возможность определить h_w для участка резко изменяющегося движения, то наличие такого участка не может препятствовать применению уравнения Бернулли.