6.1 Критерий согласия Пирсона

Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый «критерий » Пирсона. В качестве меры расхождения между эмпирическим и теоретическим распределениями в данном случае выбирается сумма квадратов разностей между эмпирическим и теоретическим значением вероятности попадания случайной величины в заданный интервал, взятых с некоторыми «весами» 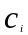: , (6.1)

где - эмпирическая вероятность попадания случайной величины в

i-тый интервал;

- теоретическая вероятность попадания случайной величины в этот интервал;

- коэффициенты пропорциональности («веса» разрядов). Эти коэффициенты вводятся потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение - может быть малозначительным, если сама вероятность велика, и очень заметным, если она мала. Пирсон показал, что если положить 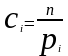, (6.2)

то при больших n закон распределения величины U обладает весьма простыми свойствами: он практически не зависит от функции распределения F(x) и от числа опытов n, а зависит только от числа разрядов k, а именно , этот закон при увеличении n приближается к так называемому «распределению ».

При таком выборе коэффициентов мера расхождения обычно обозначается : 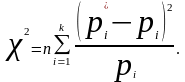(6.3)

Для удобства вычислений (чтобы не иметь дело с дробными величинами с большим количеством нулей), введём n под знак суммы, и, учитывая, что 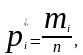где 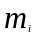- число экспериментальных данных, попавших в i-тый интервал, приведём (6.3) к виду:

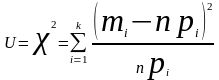. (6.4)

Распределение зависит от параметра r, называемого числом «степеней свободы» распределения. Число степеней свободы r равно числу разрядов k минус число независимых условий («связей») s, наложенных на частоты : 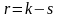. (6.5)

Примерами таких условий могут быть 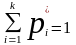, если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);

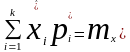, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статистическое средние значения;

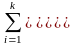, если мы требуем, кроме того, совпадения теоретической и статистической дисперсий и т.д.

Использование критерия позволяет оценить, насколько хорошо выбранная теоретическая функция распределения описывает экспериментальные данные. Действительно, в этом случае по полученному значению меры расхождения (по значению ) по таблице определяют вероятность того, что за счёт случайных причин расхождение между теоретическим и эмпирическим распределениями не меньше, чем получившееся в данной серии опытов. Если эта вероятность весьма мала (настолько мала, что событие с такой вероятностью можно считать практически невозможным), то результат опыта можно считать противоречащим гипотезе Н о том, что закон распределения величины Х есть F(x). Эту гипотезу следует отбросить как неправдоподобную. Если же эта вероятность сравнительно велика, то можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счёт случайных причин. В этом случае гипотезу Н о том, что величина Х распределена по закону F(x), можно считать правдоподобной, или, по крайней мере, не противоречащей опытным данным.

Схема применения критерия к оценке согласованности теоретического и статистического распределений сводится к следующему: 1. По формуле (6.4) определяется мера расхождения .

2. По формуле (6.5) определяется число степеней свободы r.

3.По r и с помощью таблицы определяется вероятность того, что величина, имеющая распределение с r степенями свободы, превзойдёт данное значение . Если эта вероятность относительно велика, гипотезу можно принять не противоречащей опытным данным.

Вопрос о выборе граничного значения вероятности, при которой гипотеза отбрасывается как неправдоподобная, решается в каждом конкретном случае. На практике, если это значение вероятности оказывается меньше чем 0,1, рекомендуется проверить эксперимент или повторить его. Если повторение даёт тот же результат, то считается, что принятый закон F(x) не подходит для описания изучаемых статистических данных.

Следует отметить, что успешное применение критерия возможно только при наличии достаточно обширного статистического материала

( число наблюдений n должно составлять несколько сотен). Кроме того, число экспериментальных данных внутри каждого интервала должно быть не менее 5-10. Если на практике окажется что в некоторые интервалы попало меньшее число экспериментальных данных, то рекомендуется объединять соседние интервалы.

Чтобы избежать применения таблиц для оценки соответствия экспериментальных данных выбранному закону распределения, часто пользуются критерием В. И. Романовского. Согласно этому критерию расхождения между теоретической и эмпирической функциями распределения существенны, если выполняется условие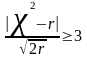 . (6.6)

И расхождения следует признать случайными, если 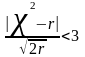. (6.7)

Следовательно, гипотеза принимается при значении критерия Романовского меньше трёх и отбрасывается в противном случае.