3.2. Изменение параметров потока в прямом скачке. Ударная адиабата

Для установления количественной зависимости параметров потока за скачком , , и от параметров потока до скачка , , и воспользуемся общими уравнениями физики: уравнением сохранения массы, уравнением изменения количества движения и уравнением энергии (Бернулли).

Уравнение сохранения массы для движения в цилиндрической трубе, в которой площадь поперечного сечения постоянна, имеет вид

.

Уравнение изменения количества движения при отсутствии объемных сил и поверхностных сил вязкости

.

Для теплоизолированного течения идеального газа уравнение Бернулли выражает закон сохранения энергии. Полагая, что скачок происходит без теплообмена с внешней средой можно записать

. (2.22)

Найдем вначале соотношение между скоростями перед и за скачком. Для этого уравнение изменения количества движения разделим на уравнение сохранения массы, получим

.

Записав уравнение энергии (2.22) до и после скачка в виде

и ,

получим из этих уравнений отношение давлений к плотностям

и .

Подставим последние выражения в уравнение энергии

.

Так как , то, разделив на и выполнив преобразования, получим

(2.23)

или

.

Формулу (2.23) называют формулой Прандтля.

Поскольку , то из (2.23) следует что, , а или . Таким образом, перед прямым скачком скорость всегда сверхзвуковая, а за скачком – дозвуковая.

Рассмотрим количественное изменение параметров потока в прямом скачке. Скачок скорости можно определить, воспользовавшись соотношением (2.23):

.

Скачок давления можно найти, используя уравнение сохранения энергии и уравнение изменения количества движения

.

Скачок плотности найдем из уравнений сохранения массы и формулы Прандтля

.

Скачок температуры находим из уравнения Бернулли, записав его в виде

,

откуда находим

. (2.24)

Приведенные формулы выражают изменения параметров потока в прямом скачке через параметр , перед скачком. Коэффициент скорости можно выразить через М по формуле

.

Заменив на в предыдущих выражениях, получим

, (2.25)

, (2.26)

, (2.27)

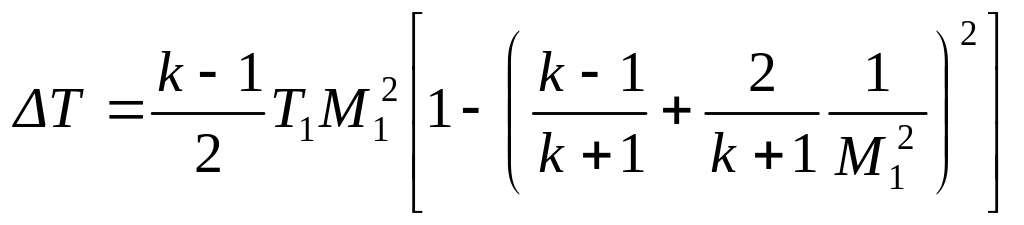. (2.28)

Из всех приведенных формул видно, что скачок параметров потока возможен только при , или . При и или скачок физически невозможен.

В таблице П2 приложения приведены значения ; ; ; для воздуха ( ) в зависимости от или , при (15С) и нормальном атмосферном давлении.

Относительное изменение плотности в скачке, как видно из выражения (2.27), может быть записано

.

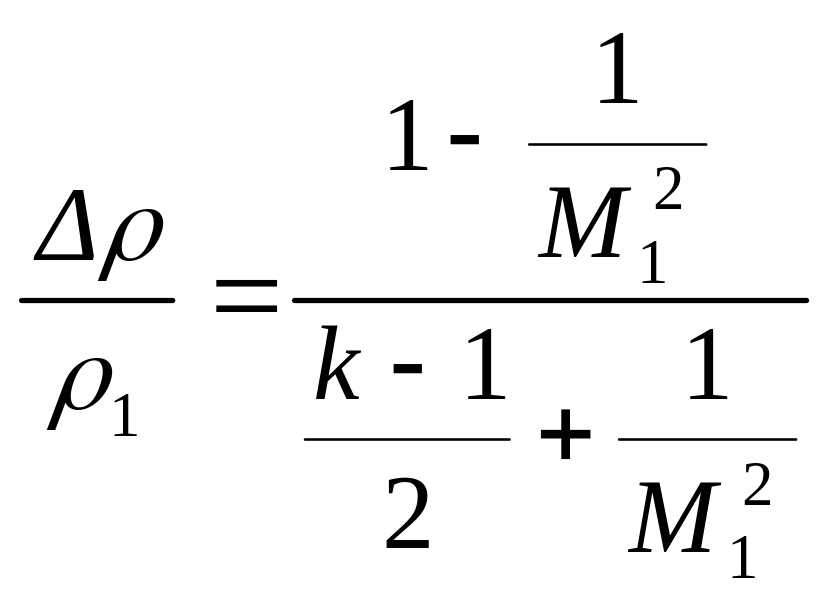Из этой формулы видно, что при стремлении числа к бесконечности имеет предел

или .

Для воздуха при .

Указанные соотношения не учитывают ионизацию и диссоциацию газа при высоких температурах. При наличии этих явлений может быть более 5. Так, при .

При адиабатическом непрерывном движении газа связь между р и определяется изэнтропической адиабатой (адиабатой Пуассона)

,

из которой видно, что при увеличении давления плотность растет неограниченно.

Установим зависимость от р в скачке уплотнения. Из уравнения (2.22) получим

. (2.29)

Воспользуемся следующей формой уравнения изменения количества движения

.

Умножая правую часть этого равенства на , а левую часть на равное значение, представленное в виде

,

получим

.

Приравнивая правую часть уравнения (2.29) к правой части последнего выражения, найдем связь между р и .

.

Группируя слагаемые с и , найдем

.

Приведя полученное выражение к общему знаменателю и умножив на , окончательно получим

. (2.30)

Уравнение (2.30) называется ударной адиабатой или адиабатой Гюгонио.

Решив уравнение (2.29) относительно , найдем

.

Из уравнения видно, что при получаем уже известное соотношение . Применив уравнение состояния к (2.30), заменим отношение плотностей отношением температур и давлений и затем, написав полученное соотношение относительно , получим

.

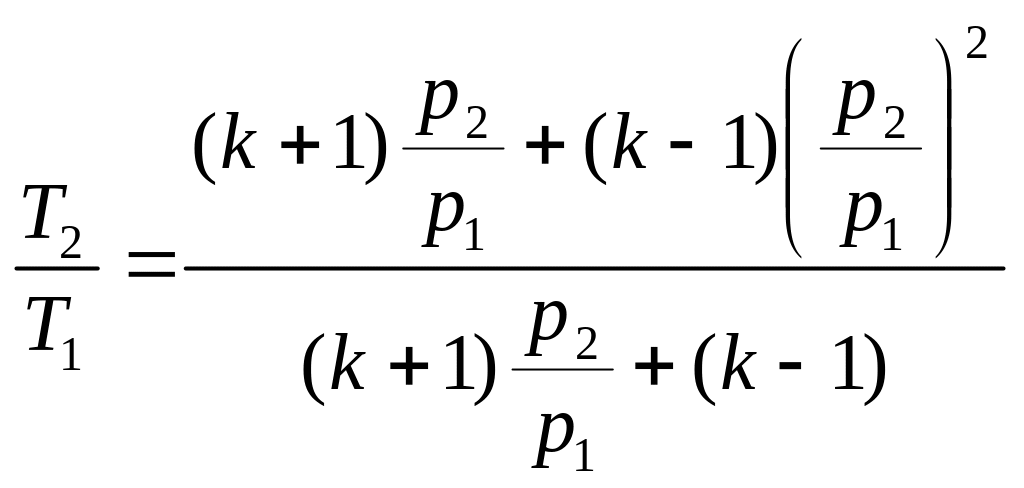Н а рисунке изображены обычная (1) и ударная (2) адиабаты. Различие их в том, что для обычной адиабаты отношение растет неогранично при увеличении . Для ударной адиабаты при увеличении отношение плотностей асимптотически приближается к пределу, равному . Это значит, что как бы не возрастало давление при переходе через скачок, уплотнение газа не может превосходить этого предела (для воздуха равного шести).

Переход через скачок является неизоэнтропийным процессом и сопровождается переходом механической энергии в тепловую.

Таким образом, прямой скачок уплотнения является формой перехода от сверхзвукового течения к дозвуковому.

В прямом скачке скачкообразно снижаются скорость потока V, число Маха M, и скоростной коэффициент . При этом происходит скачкообразное увеличение плотности , давления p и температуры T.

В прямом скачке остаются неизменными: Т₀ – температура торможения, , V_макс, а₀, i₀, .

Перед скачком справедливо равенство

,

а за ним

.

Так как на основании уравнения Бернулли левые части этих выражений равны, то равны и их правые части, откуда следует равенство .

Неизменность Т₀ при переходе через скачок объясняется тем, что часть механической энергии преобразуется в тепловую, но не рассеивается благодаря теплоизолированности процесса. Поэтому полная удельная энергия, определяемая Т₀, не меняется.

Давление торможения и плотность торможения уменьшаются на скачках.

Величина , называемая коэффициентом восстановления полного давления, характеризует собой необратимые потери механической энергии на скачке (1 – параметр до скачка, 2 – после скачка). Ее определяют по формуле

.

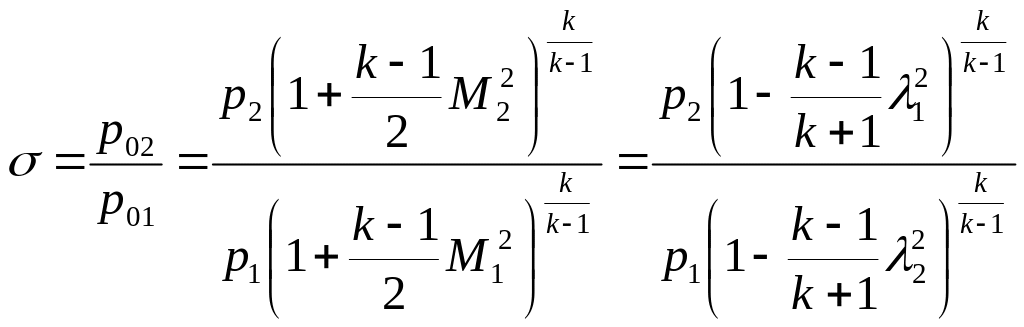Заменяя здесь отношение на одно из следующих:

и используя выражения и через и , получим искомое отношение в одном из следующих двух видов:

(2.31)

Рис. 2.4.	Рис. 2.5.

На рис. 2.4 представлен график второго соотношения (2.31) для воздуха (k = 1,4); там же приведен график сжатия для воздуха в скачке. График, выражающий первое соотношение (2.31), имеет такой же характер. Однако на нем обращается в ноль не при бесконечном значении числа Маха, а при конечном значении скоростного коэффициента, равном . Как видно из графика, чем больше величины или , характеризующие интенсивность скачка, тем относительно меньшее давление р₂₀ можно получить за счет последующего адиабатического и изэнтропического торможения газа, прошедшего через скачок уплотнения. Причина этого явления была выяснена раньше: в скачке уплотнения имеет место необратимое превращение механической энергии в тепловую, вследствие чего механическая энергия потока уменьшается.

Более точно, чем по рис. 2.4, можно судить о значениях отношения при больших числах по графику, представленному на рис. 2.5, где это отношение построено в логарифмическом масштабе. Там же изображена зависимость , которая потребуется в дальнейшем.

При больших значениях вторая из формул (2.31) может быть заменена приближенной, асимптотической зависимостью.

.

Это позволяет осуществлять простую количественную оценку поведения величины при больших числах Маха перед скачком. Например, для воздуха (k = 1,4) рассматриваемое отношение обратно пропорционально числу в пятой степени, что говорит о весьма значительных потерях механической энергии при прохождении газа через скачки большой интенсивности. Укажем, что соответствующая этому случаю, простая асимптотическая формула для (верная только при больших значениях ) будет иметь вид: .

Исследуем поведение кривой на рис. 2.5 при малых значениях разности . Преобразуем второе равенство (2.31) к виду

Производя разложение по степеням малой величины , убедимся, что коэффициенты при и обращаются в ноль, и разложение величины будет иметь вид

Из него видно, что скачки малой интенсивности не приводят к заметной потере полного напора, так как при близком к единице, совпадает с , с точностью до малой величины

.

Так, для воздуха (k = l,4) эта величина имеет порядок и, например, при превышении скорости звука на 10% ( ) будет равна 0,0015.

При наличии необратимых потерь в адиабатической системе возрастает ее энтропия. Для определения этого возрастания применим уравнение изменения энтропии, подставив в него параметры адиабатически и изэнтропически заторможенного газа. Это допустимо, так как изэнтропическое торможение не может влиять на приращение энтропии. Получим

.

Используя равенство , получим

.

Подставляя сюда отношение по приближенной формуле, найдем при больших M₁ соотношение

,

выражающее асимптотический закон роста энтропии при прохождении газа сквозь скачки большой интенсивности.

При сравнительно малой интенсивности, т.е. при разности , близкой к нулю, будем иметь

.

Отсюда следует, что скачки малой интенсивности приводят к слабым изменениям энтропии, т. е. околозвуковые явления можно с достаточной степенью приближения рассматривать как изэнтропические.